Відрізки та їх вимірювання
Розділ 1. Найпростіші геометричні фігури та їх властивості
§ 2. Відрізки та їх вимірювання
28. 1) Кінці відрізка MN: М і N; внутрішні точки: А, О, В. 2) Кінці відрізка AN: A i N; внутрішні точки: О i B. 3) Кінці відрізка AB: А і В; внутрішня точка: О.
29. 
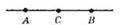
Утворилося три відрізки: AB, АС, ВС.
30.
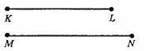
KL = 3,5 см; MN = 4 см; KL < MN.
31. 1)
AB = 3,5 см = 35 мм; CD = 42 мм; AB < CD.
2)
AB = 50 мм; CD = 0,5 дм = 50 мм; АВ = CD.
32. 
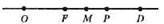
OP = AB; OF = BC;
33. 
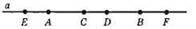
Утворилися відрізки: AE, CE, DE, BE, FE, AC, AD, AB, AF, CD, CB, CF, DB, DF, BF.
34. 1) АС = 3 см, BD = 20 мм = 2 см, KL = 0,3 дм = 3 см. AC = KL > BD.
2) AC = 0,01 дм = 0,1 см, BD = 10 см, KL = 1 мм = 0,1 см. AC = KL < BD.
3) AC = 4,2 мм = 0,42 см, BD = 0,42 дм = 4,2 см, KL = 0,42 см. AC = KL < BD.
35. PO = PT + TQ = 0,3 дм + 30 мм = 3 см + 3 см = 6 CM.
36. 
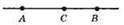
AB > АС, оскільки відрізок АС є частиною відрізка AB.
37. 
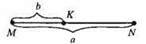
1) KN = MN – MK = a – b = 6 cм – 4,5 cм = 1,5 см.
2) KN = а – b = 0,3 дм – 20 мм = 3 см – 2 см = 1 см.
3) KN = а – b = 40 мм – 1,5 см = 4 см – 1,5 см = 2,5 см.
38. 
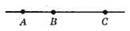
АС | 10 | 6,7 см | 2,2 дм |
AB | 5,5 см | 4,3 см | 16 см |
ВС | 45 мм | 2,4 см | 6 см |
АС = АВ + ВС = 5,5 см + 45 мм = 5,5 см + 4,5 см = 10 см.
AB = АС – ВС = 6,7 см – 2,4 см = 4,3 см.
ВС = АС – AB = 2,2 дм – 16 см = 22 см – 16 см = 6 см.
39. 1) Якщо точка С між точками А і В, то AB = АС + СВ. Але 5 см ≠ 11 см + 6 см. Отже, точка С не лежить між точками А і В. 2) Якщо точка С лежить між точками А і В, то AB = АС + СВ. Оскільки 12 CM = 3,5 CM + 8,5 см, то точка С лежить між точками А i B.
40. 1) Якщо точка В лежить на відрізку АС, To AC = AB + BC. Але 10cм ≠ AB + 14 см. Отже, точка В не лежить на відрізку АС. 2) Якщо точка В лежить на відрізку АС, то АС = AB + BC. Оскільки 11 см = 4 см + 7 см, то точка В лежить на відрізку АС.
41. 1) Якщо точки А, В, С лежать на одній прямій, то найбільший із відрізків АС, AB, ВС дорівнює сумі двох інших. Оскільки за умовою найбільший із заданих відрізків AB = 17 см, а сума двох інших АС + ВС = 6,5 см + 10,5 см = 17 см, то точки А, В, С лежать на одній прямій. 2) Якщо точки А, В, С лежать на одній прямій, то найбільший з відрізків АС, AB, ВС дорівнює сумі двох інших. Оскільки за умовою найбільший відрізок дорівнює 1,5 дм, а сума двох інших АС + ВС = 0,6 дм + 1 дм =1,6 дм. 1,5 дм ≠ 1,6 дм, то точки А, В, С не лежать на одній прямій.
42. 1)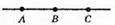 
На промені ВА від його початку можна відкласти тільки один відрізок даної довжини.
2) На доповняльних променях BA i ВС від їх спільного початку можна відкласти два відрізки даної довжини (один на промені ВА і один на промені ВС).
43.
АВ | 9 см | 86 мм | 16,6 мм |
АО | 4,5 см | 43 мм | 8,3 мм |
OB | 4,5 см | 43 мм | 8,3 мм |
AB | 0,9 дм | 0,86 дм | 0,166 дм |
AO | 0,45 дм | 0,43 дм | 0,083 дм |
OB | 0,45 дм | 0,43 дм | 0,083 дм |
AB | 0,09 м | 0,086 м | 0,0166 м |
АО | 0,045 м | 0,043 м | 0,0083 м |
OB | 0,045 м | 0,043 м | 0,0083 м |
44. 
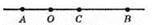
Якщо AB = 8 см, то
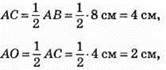
OB = АВ – АО = 8 см – 2 см = 6 см.
Відповідь: АО = 2 см; OB = 6 см.
45. 
1) Точка Z) лежить на відрізках: AE, AD, BE, СЕ, BD, CD, ED.
2) Точка С не лежить на відрізках AB і DE.
46.
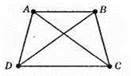
Існує шість відрізків з кінцями в точках А, В, С, D: AB, AC, AD, ВС, CD, BD.
47. 
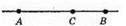
Нехай ВС = х см, тоді АС = 3х см. За властивістю вимірювання відрізків маємо: AB = АС + ВС, х + 3х = 8; 4х = 8; х = 2. Отже, ВС = 2 см, АС = 3 x 2 = 6 (см).
Відповідь: 2 см і 6 см.
48. AB = CD за умови, що ВС = BD.
49. 1) Оскільки ВС = 2 дм = 20 см, a AB + АС= 16 см + 4 см = 20 см, тобто виконується умова ВС = AB + АС, то точка А лежить між точками В і С.
2) Оскільки AB + ВС =АС, то точка В лежить між точками А і С.
3) Оскільки ВА + АС = ВС, то точка А лежить між точками В і С.
4) Оскільки BA = BC – AC, то BC = BA + AC. Отже, точка А лежить між точками В і С.
50. Оскільки AM + MB = AB, то точка М лежить між точками А і В. Оскільки AM = MB, то точка М – середина відрізка AB.
51. 1)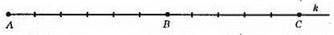 
АС = AB + ВС = 6 см + 5 см = 11 см.
2) 
АС = АВ – ВС = 6 см – 5 см = 1 см.
52. а)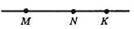 
МК = MN + NK =14 + 16 = 30 (см);
Б)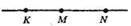 
МК = NK – MN = 16 – 14 = 2 (см).
Відповідь: 30 см або 2 см.
53. 1) 
ВС = АС – ВА = 40 мм – 30 мм = 10 мм.
2) AN = NC = АС : 2 = 40 мм : 2 = 20 мм;
АК = КВ =АВ : 2 = 30 мм : 2 = 15 мм;
KN = AN – АК = 20 мм – 15 мм = 5 мм.
Відповідь: 1) 10 мм; 2) 5 мм.
54. 
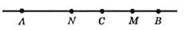
Нехай AB = 18 см, АС, ВС – частини відрізка AB, N – середина відрізка АС, М – середина відрізка ВС.
NC = 1/2АС, СМ = 1/2ВС, тоді
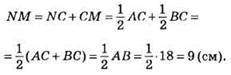
Відповідь: 9 см.
55. 
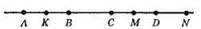
Точка К – середина відрізка AB,
КВ = і AB = і – 2 см = 1 см.
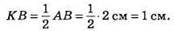
Точка М – середина відрізка CD,
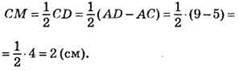
KM = KB + ВС + CM = 1 см + 3 см + 2 см = 6 см.
Відповідь: 6 CM.
56. 
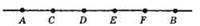
Утворилося п’ять відрізків, що мають не більше ніж одну спільну точку.
57. Оскільки точки А, В, С лежать на одній прямій і точки В, С, D лежать на одній прямій, то ці прямі мають спільні точки В і С. Згідно з властивістю прямої, ці прямі збігаються. Отже, точки А, В, С і D лежать на одній прямій.
58. Нехай відрізок AB лежить на прямій а, а відрізок CD лежить на прямій b. Оскільки відрізки AB і CD мають дві спільні точки, то і прямі а і b мають також дві спільні точки. Тоді, згідно з властивістю прямої, прямі а і b збігаються. Отже, відрізки AB і CD лежать на одній прямій.
59. а)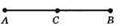 
Утворилося 3 відрізки: AB, АС, ВС;
Б) 
Утворилося 6 відрізків: АС, AD, AB, CD, CB, DB;
В)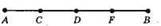 
Утворилося 10 відрізків: АС, AD, AF, AB, CD, CF, CB, DF, DB, FB.
2) Якщо на відрізку вказано n точок, то всього утвориться (n + 1) + n + (n – 1) + … + 2 + 1 відрізків або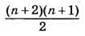 
відрізків.
60. а) 
BD = BC + CD = BC + AB = АС = 5 см;
Б) 
BD = CD – ВС = АВ – BC = AC = 5 см.
Відповідь: 5 см.
61. 
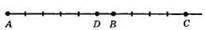
1) DB = AB – AD = AB – (AC – CD) = AB – AC + CD = 6 – 10 + 5 = 1 (см).
2) AD = AC – CD = 10 – 5 = 5 (см).
Відповідь: 1) 1 см; 2) 5 см.
62. 
Точка М – середина відрізка АС, тоді MC = 1/2АС. N – середина відрізка СВ, тоді CN = 1/2СВ.
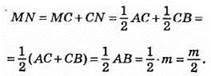
Відповідь: m/2.
63. 
M – середина відрізка АС, тоді АС = 2MC. N – середина відрізка СВ, тоді CB = 2CN.
AB = АС + СВ = 2MC + 2CN = 2(MC + CN) = 2 x MN = 2 x n = 2n.
Відповідь: 2n.
64. 
AM + NB = AB – MN = 16 – 14 = 2 (см).
CD = MN – MC – DN = MN – (MC + DN) = MN – (AM + NB) = 14 – 2 = 12 см.
Відповідь: 12 см.
65. 
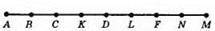
За умовою AB = BC, CK = KD, DL = LF, FN = NM, AM = 24 см, BN = 20 см.
AB + NM = AM – BN = 24 – 20 = 4 (см).
BC + FN = 4 см.
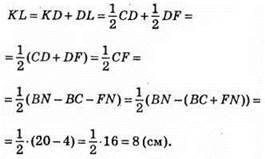
Відповідь: 8 см.
66. 1) Розглянемо три випадки:
A)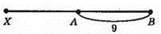 
Шукана точка лежить ліворуч від т. А, тоді 2АХ = ХВ, або 2АХ = АХ +АВ. Враховуючи, що АВ = 9 см, маємо: 2АХ – АХ = 9, АХ = 9 см;
Б)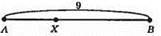 
Якщо шукана точка лежить між точками А і В, тоді 2АХ = ХВ, 2АХ = AB – АХ, 3АХ = АВ, 3АХ = 9, АХ = 3 см;
В) 
Якщо точка X лежить праворуч точки В, то такий випадок неможливий, бо АХ = АВ + ВХ, тобто АХ > ВХ, а за умовою АХ < ВХ.
2) Розглянемо три випадки:
А) 
Випадок (шукана точка X розташована ліворуч точки А) неможливий, бо АХ + ВХ = АХ + АХ + АВ = 2АХ + АВ = 2АХ + 8, тобто АХ + ВХ > 8 см;
Б)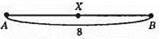 
Нехай точка X лежить між точками А і B, тоді АХ + ВХ = АВ = 8. Отже, будь-яка внутрішня точка відрізка AB буде шуканою.
В)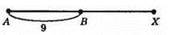 
Випадок (шукана точка X розташована праворуч точки В) неможливий, бо АХ + ВХ = AB + ВХ + ВХ = AB + 2 ВХ = 8 + 2 ВХ, тобто АХ + ВХ > 8 см.
3) Розглянемо три випадки:
А) 
Випадок (шукана точка X знаходиться праворуч від точки А) неможливий, бо ХА – ХВ = ХА + AB – ХА = AB, але за умовою ХВ – ХА = 2 см, а AB = 14 см.
Б)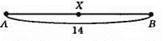 
Нехай точка X розташована між точками А і В. Якщо ХВ – ХА = 2 см, тоді АВ – ХА – ХА = 2,14 – 2ХА = 2; 2ХА = 14 – 2; 2ХА = 12; ХА = 6 см.
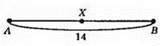
Якщо ХА – ХВ = 2 см, тоді ХА – (АВ – ХА) = 2,2ХА – АВ = 2; 2ХА – 14 = 2; 2ХА = 16; ХА = 8 см.
В)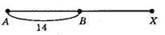 
Випадок (шукана точка X знаходиться праворуч точки В) неможливий, бо ХА – ХВ = AB + ХВ – ХВ = AB, але за умовою ХВ – ХА = 2 см, а AB = 14 см.
67. Відстань від Києва до Сум дорівнює 480 км – 140 км = 340 км.
69. 1) Людина перебуває на відстані менше 5 км і більше 4 км від будинку;
2) Людина перебуває на відстані менше 4 км і більше 3 км від будинку.
(1 votes, average: 5.00 out of 5)
Loading...