Головна ⇒ 📌Довідник з геометрії ⇒ Відстань між точками
Відстань між точками
Геометрія
Декартові координати на площині
Відстань між точками
Якщо 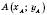 ,
, 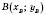 – довільні точки і AB відстань між ними, то
– довільні точки і AB відстань між ними, то
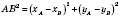 або
або
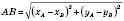 .
.
У випадку, коли точка B збігається з початком координат 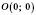 , отримуємо:
, отримуємо:
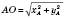 .
.
Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними x і y, яке задовольняють координати будь-якої точки фігури й тільки вони.
Related posts:
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Відстань між двома точками простору Урок 45 Тема. Відстань між двома точками простору Мета уроку: виведення формул для знаходження відстані між двома точками, заданих координатами, та застосування формули до розв’язування задач. Обладнання: схема “Відстань між двома точками”, модель куба. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Ребро куба дорівнює 10: варіант 1 […]...
- Відстань між двома точками із заданими координатами УРОК № 24 Тема. Відстань між двома точками із заданими координатами Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і доводять формулу для знаходження відстані […]...
- Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...
- Рівняння прямої Геометрія Декартові координати на площині Рівняння прямої Будь-яка пряма в декартових координатах x, y має рівняння виду: , де a, b, c – деякі числа. Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі “Алгебра. 8 клас” (“Лінійна функція”). Рівняння прямої, яка перетинає осі координат в точках і , […]...
- Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...
- Відстань між мимобіжними прямими Геометрія Стереометрія Відстань між мимобіжними прямими Спільним перпендикуляром до двох мимобіжних прямих називається відрізок із кінцями на цих прямих, перпендикулярний до кожної з них. Теорема. Дві мимобіжні прямі мають спільний перпендикуляр, і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. Відстанню між мимобіжними прямими називається довжина […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Координати – Кінематика 5. Механіка 5.1. Кінематика 5.1.5. Координати Координати точки – це числа, які визначають положення фізичного тіла (матеріальної точки) на площині чи в просторі. В декартовій системі координат положення тіла (матеріальної точки) на лінії площини і в просторі визначається відповідно однією (а), двома (б) або трьома (в) координатами (X, Y, Z)....
- Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Урок 35 Тема. Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Мета уроку: формування вмінь учнів застосувати теорему про три перпендикуляри до розв’язування задач, знаходження відстані від точки до прямої. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Два учні відтворюють на дошці розв’язування задач № 13, 41. […]...
- Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...
- Рівняння кола Геометрія Декартові координати на площині Рівняння кола – рівняння кола з центром у точці і радіусом R. Зверніть увагу: рівняння , де , задає коло й може бути зведеним до стандартного виду....
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Координати середини відрізка Геометрія Декартові координати на площині Координати середини відрізка Якщо , – довільні точки, – середина відрізка AB, то ; ....
- Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Рівняння із двома змінними та його розв’язок Урок № 69 Тема. Рівняння із двома змінними та його розв’язок Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати […]...