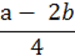ВИРАЗИ ЗІ ЗМІННИМИ
РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ
&2. ВИРАЗИ ЗІ ЗМІННИМИ
Подивіться на малюнок 2. Ви бачите спортсменів па змаганнях з потрійного стрибка. Виконуючи три елементи такого стрибка (скачок, крок і стрибок), кожен спортсмен долає відстані, властиві тільки йому, а сума цих відстаней складає довжину стрибка. Якщо позначити ці відстані буквами а, b і с, то для довжини потрійного стрибка дістанемо вираз: а + b + с. Ви знаєте, що де – буквений вираз. Для кожного спортсмена відстані, позначені буквами а, b і с, є різними, і вони можуть змінюватися залежно
Мал. 2
Чи кожен буквений вираз є виразом зі змінними? Ні. Наприклад, ви знаєте, що буквою п позначають відношення довжини кола до його діаметра. Але це число є сталим для будь-якого кола і не може змінюватися, воно є константою: п ≈ 3,14. Тому буквений вираз, наприклад 2п, не є виразом зі змінною. Пізніше в курсі математики і фізики ви ознайомитесь і з іншими константами.
Запам’ятайте!
Запис, у якому використовують змінні, позначені буквами, числа, знаки арифметичних
Саму змінну також вважають виразом зі змінними. І це найпростіший із таких виразів. Наприклад, довжину сторони квадрата можна подати так: а.
Замість змінних, що входять до виразу, можна підставити числа – значення змінних. Тоді вираз зі змінними перетвориться на числовий вираз. Викопавши обчислення, дістанемо число, яке називають значеннями виразу для заданих значень змінних. Наприклад, вираз 2(а + b) використовують для обчислення периметра прямокутника зі сторонами а і b. Звідси:
Якщо а = 1 і b = 3, то 2(а + b) = 2 ∙ (1 + 3) = 8;
Якщо а = 5 і b = 2, то 2(а + b) = 2 ∙ (5 + 2) = 14;
Якщо а = 3,5 і b = 6,1, то 2(а + b) = 2 ∙ (3,5 + 6,1)= 19,2 і т. д.
Зверніть увагу:
Значення виразу зі змінними залежить від значень змінних, що входять до нього.
? Чи завжди можна обчислити значення виразу зі змінними? Ні. Наприклад, якщо х = 2, то вираз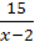 
втрачає зміст, оскільки його знаменник перетворюється на 0, а на 0 ділити не можна. Отже, число 2 є недопустимим значенням змінної для даного виразу. Будь-яке інше число не перетворює на нуль знаменник даного виразу і тому є допустимим значенням змінної для нього. Отже, вираз 
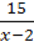має зміст, лише якщо х ≠ 2.
Усі значення змінної, допустимі для даного виразу, утворюють область допустимих значень (ОДЗ) змінної цього виразу. У розглянутому прикладі – це всі значення змінної х, що не дорівнюють 2.
Коротко це записують так: ОДЗ: х ≠ 2.
Вирази зі змінними можна поділити на види залежно від тих дій, які містяться в цих виразах. Якщо вираз містить лише дії додавання, віднімання, множення, ділення і піднесення до степеня з натуральним показником, то такий вираз називають раціональним. Усі вирази, які розглядались у цьому параграфі, є раціональними. У наступних класах ви ознайомитесь і з іншими діями, наявність яких у виразі робитиме його ірраціональним.
Раціональні вирази, своєю чергою, поділяються на цілі та дробові вирази.
Запам’ятайте!
Вираз називається цілим, якщо він не містить ділення на вираз зі змінними.
Наприклад, цілими є вирази: (2 + а) : 30,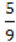
х, – b + 
.
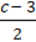Прикладами дробових виразів є вирази: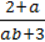 
, (b – а) : (a – 5b + 3). Дробові вирази ви будете вивчати пізніше.
Задача. Які значення змінних є допустимими для виразу:
1) 
;
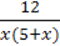2) 
?
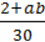Розв’язання. 1) Вираз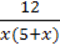 
містить ділення на добуток двох множників х і 5 + х, які перетворюють знаменник на нуль, якщо х = 0 і х = -5 відповідно. Отже, числа 0 і -5 є недопустимими значеннями змінної х для даного виразу. Відтак ОДЗ: х ≠ 0, х ≠ 5.
2) Вираз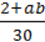 
містить ділення на число, але не містить ділення на вираз зі змінними. Отже, це – цілий вираз, тому для нього будь-які значення змінних а і b є допустимими. Відтак ОДЗ: а – будь-яке число, b – будь-яке число.
Зверніть увагу:
Для цілого виразу ОДЗ кожної змінної – будь-яке число.
Дізнайтеся більше
Алгебра – одна з провідних галузей сучасної математики, а також один із предметів шкільного навмання. Слово αλδψεβρ уперше зустрічається у творі Аль-Хорезмі (IX ст.). Цей твір був присвячений розв’язуванню рівнянь першого і другого степенів. Пізніші переклади зробили слово αλδψεβρ назвою всієї науки “алгебри”, яка довгий час була наукою про рівняння.
Зародження алгебри слід віднести до тих часів, коли в арифметику почали вводити невідому величину і спеціальний символ для її позначення, формулювати загальні правила розв’язування арифметичних задач певного типу й у зв’язку з цим складати й розв’язувати рівняння. У цьому розумінні певні алгебраїчні факти були відомі ще в Стародавніх Вавилоні та Єгипті, в Індії та Китаї.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що називається виразом зі змінними? Наведіть приклади.
2. Поясніть, як обчислити значення виразу зі змінними.
3. Що таке допустимі значення змінної для виразу зі змінними?
4. Які вирази називають раціональними?
5. Які вирази називаються цілими?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
49. Прочитайте вираз:
1)5a + 6b;
2)15 ∙ 2,4 + 17;
3)m + 25n;
4)42 + 43;
5 )abc;
6) 
.
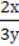Чи є даний вираз виразом зі змінними? Відповідь поясніть.
50. Значення виразу 3х – 2у дорівнює 1, якщо х = 5 і у = 7. Назвіть: 1) вираз зі змінними; 2) змінні у виразі; 3) значення виразу; 4) значення змінних. Чи зміниться значення даного виразу, якщо змінити значення: а) змінної х на -0,5; б) змінної у на 8; в) змінної х на 2, а змінної у на -2?
51. Дано вираз: (х – 5): (х + 7). Чи є допустимим для даного виразу таке значення змінної х:
1) -5; 2) 5; 3)7; 4)-7?
Назвіть ОДЗ змінної даного виразу.
52. Чи є данний вираз цілим:
1) а + 4,5b;
2) 
;
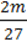3)(m – n) : 5n;
4) 
;
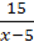5)
;
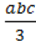6) 
X + 
Відповідь: поясніть.
53. Дано вираз: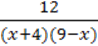 
. Чи правильно визначено ОДЗ його змінної:
1)х ≠ -4; 3) x ≠ 12; 5) х ≠ 4, х ≠ 9.
2)х ≠ 9; 4) х ≠ 4, х ≠ -9; 6) х ≠ -4, х ≠ 9.
Відповідь поясніть.
54. Чи правильно, що значення виразу 2а + 10 дорівнює 0, якщо:
1) а = 2; 2) а = -5; 3) а = 0,5; 4)а = 0?
55. Олег стверджує, що можна обчислити всі значення виразу 4а – 12. Чи правий Олег?
56. Запишіть у вигляді виразу: 1 )суму змінних а і b, 2) частку змінних с і d; 3) квадрат змінної р; 4) потроєну суму змінної h і числа 8; 5) різницю подвоєної змінної а і змінної b; 6) суму змінної а і різниці змінної b і числа 5; 7) частку від ділення числа 12 на суму змінних а і b; 8) добуток числа 5 та суми змінних n і m; 9) частку від ділення суми змінної а і числа 10 на різницю змінної b і числа 8; 10) суму потроєної змінної х і подвоєної змінної у.
57. Запишіть у вигляді виразу: 1) добуток змінних а і b; 2) різницю змінних с і d; 3) суму добутку числа 7 і змінної а та частки відділення числа 9 на змінну b; 4) суму потроєної змінної с і числа 7; 5) різницю числа 10 і добутку числа 5 і змінної с; 6) добуток квадрата змінної х і куба змінної y.
58. За даними таблиці 1 знайдіть значення виразів.
Таблиця 1
А | 10 | 8,4 |
|
|
B | -5 | 4,8 |
| 10 |
2а +0,5b | ||||
|
59. Заданими таблиці 2 знайдіть знамення виразів.
Таблиця 2
С | 9 | 3,6 | 2,25 | 0,81 |
D | -50 | 3 | -8 | 0,125 |
|
60. У 7-А класі навчаються а учнів, у 7-Б класі – на 2 учні більше, ніжу 7-А класі, а в 7-В – на 5 учнів менше, ніж у 7-Б класі. Скільки учнів навчаються в усіх сьомих класах разом? Складіть вираз для розв’язування задачі та знайдіть його значення для:
1) n = 17;
2) n = 22.
61. Зошит коштує а грн, а блокнот – на 7 грн більше. Скільки коштують 5 таких зошитів і 10 блокнотів разом? Складіть вираз для розв’язування задачі та знайдіть його значення для а = 3.
62. Чи всі значення змінної а є допустимими для виразу:
1)5а + 4;
2)
;
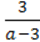3) 
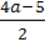
4) 
;
5)1,5(а + 10);
6) 
?
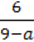Відповідь поясніть.
63. Чи всі знамення змінної b є допустимими для виразу:
1)12 – 6b;
2)
;
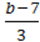3) 
;
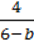4) 
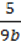
64. У числовому виразі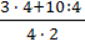 
замініть число 4 на букву а. Чи всі значення змінної а є допустимими для отриманого виразу?
65. У числовому виразі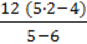 
замініть число 5 на букву b.
Чи всі значення змінної Ь є допустимими для отриманого виразу?
66. Чи правильно, що лише для х + 4 має зміст вираз:
1) 
;
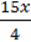2) 
;
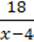3) 
;
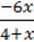4) 
.
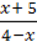Відповідь обгрунтуйте.
67. Чи є цілим вираз:
1) 
;
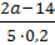2) 
;
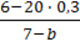3) 
;
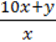4) 
.
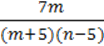Відповідь обгрунтуйте.
68. Чи є цілим вираз:
1) 
;
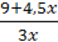2) 
;
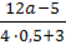Відповідь обгрунтуйте.
69. Чи всі значення змінних є допустимими для виразу:
1) 2a – b + 3c;
2) 
;
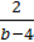3) 
;
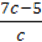4) .
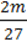5) 
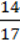(a + b);
6) 
?
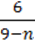70. Чи всі значення змінних є допустимими для виразу:
1) 4a – 6b;
2) 
;
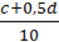3) 
;
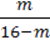4) 
(p + 6n)?
71. Укажіть ОДЗ змінних виразу та обчисліть його значення:
1) 6а + 4b для а = 
, b = -0,25;
2) 0,4с – 4d2 + 4,5 для с = -20, d = 
;
3) 
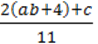Для а = -2,8, b = 
,с = 0,4;
4) 3,5 – 5 (m2 – 1) + 1,2(4p –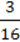 
) для n = 2, m = 0,5, p = 1 
;
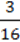5) 
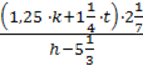для k = 1
, l = -1, h = 1,5;
6) 
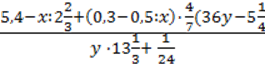Для х = 4, у = 
.
72. Укажіть ОДЗ змінних виразу та обчисліть його значення:
1)-5,4а + 6b – 12 для а= 
, b = -0,15;
2) 5(2,5n2 – n) – 9(р – 2 
) для n = 0,2, m =-2,8, р = -4 
;
3) 
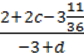для c = 
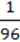, d = –
;
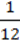4) (
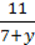– 2x ∙ 12,5 + 1 
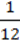) : 0,017 – 0,5 ∙ 105 для x = , y = 
.
73. Автомобіль рухається зі швидкістю 60 км/год. Складіть вираз для знаходження відстані, яку проїде автомобіль за t год. Знайдіть значення виразу, якщо:
1)t = 4 год; 3) t = 2 год 30 хв;
2)t = 4 год 30 хв; 4) t = 5 год 20 хв.
74. Одна сторона прямокутника дорівнює а см, а інша – на 5 см більша. Складіть вирази для знаходження периметра і площі прямокутника. Знайдіть значення цих виразів, якщо:
1)а = 2см; 3)а = 3дм;
2)а = 5см; 4) а =6 см 4 мм.
75. Складіть вирази для знаходження периметра і площі квадрата зі стороною с. Знайдіть значення цих виразів, якщо:
1)с = 3 см; 2) c = 4см 5мм.
76. Відомо, що для деяких значень х і у значення виразу х – у дорівнює 6,2. Якого значення за тих самих значень х і у набуває вираз:
1) 4х – 4у;
2) у – х;
3) 0,25(2y – 2x);
4) 
.
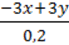77. Відомо, що для деяких значень с і d значення виразу с + d дорівнює . Якого значення за тих самих значень с і d набуває вираз:
1) 6c + 6d – 6;
2) 
?
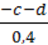78. Відомо, що a + 3b = 6 і с = 4. Знайдіть значення виразу:
1)а + 3(b + с);
2) 6b + 2(а – 5с);
3) 
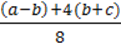
79. Запишіть число, яке: 1) є наступним для натурального числа n; 2) дорівнює добутку трьох послідовних чисел, найбільше з яких m; 3) у своєму записі має а тисяч, b сотень, с десятків і d одиниць.
80. Знайдіть значення у, за яких дріб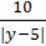 
:
1) дорівнює 10; 2) не має змісту.
81.Знайдіть ОДЗ змінних виразу:
1) 
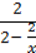; 2)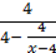 
.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
82. Складіть вираз для обчислення кількості учнів у 7 класі, у якому навчаються а хлопців та b дівчат. Обчисліть значення цього виразу за даними вашого класу.
83. На придбання меблів для кабінету виділено кошти. Розрахуйте варіанти мінімальної та максимальної вартості комплекту, що містить а столів, b стільців, с шаф та d стелажів, якщо вартість столів становить 450-550 грн, стільців – 120-135 грн, шаф – 1200-1500 грн, стелажів – 800-950 грн. Урахуйте, що для оптових покупців діє знижка 10%. Обчисліть вартість покупки, якщо а = 6, b = 6, с = 1, d = 3.
ЗАДАЧІ НА ПОВТОРЕННЯ
84. Обчисліть:
1) 5% числа 55; 3) 120 % числа 4,5;
2) 60 % числа 30; 4) 72 % числа 3 
.
85. Знайдіть число:
1)8% якого дорівнюють 24;
2) 9 % якого дорівнюють 8,1;
3) 13 % якого дорівнюють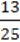 
;
4) 105 % якого дорівнюють 21.
(1 votes, average: 5.00 out of 5)
Loading...