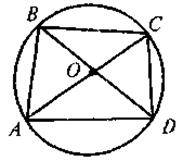
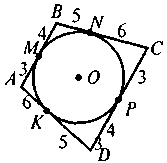
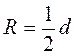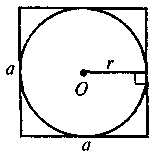Вписані чотирикутники. Описані чотирикутники
Урок № 22
Тема. Вписані чотирикутники. Описані чотирикутники
Мета: працювати над засвоєнням учнями змісту понять: чотирикутник, вписаний у коло; чотирикутник, описаний навколо кола; розглянути зміст теорем про вписаний та описаний чотирикутники та схеми їх доведення.
Сформувати вміння:
– відтворювати вивчені твердження;
– виконувати рисунок за описом;
– використовувати вивчені теореми під час розв’язування теореми на чотирикутники.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання:
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
З метою економії часу перевірка домашнього завдання проводиться у формі бесіди за готовими рисунками (рисунки до домашніх задач учитель виконує на дошці заздалегідь; також можна записати схеми розв’язання задач). Бесіда проводиться під керівництвом учителя, який ставить питання на розуміння учнями обгрунтування основних етапів розв’язання задач.
III. Формулювання мети і завдань уроку
Учитель нагадує про складену на 20-му уроці схему, в якій відображено логіку викладення
IV. Актуалізація опорних знань
Для успішного засвоєння учнями означення, властивості, ознаки та способів доведення теорем про вписаний та описаний чотирикутники слід активізувати знання і вміння учнів щодо означення та властивості дотичної до кола та наслідку з неї (властивість відрізків дотичних); теореми про бісектрису кута.
Виконання усних вправ за готовими рисунками
1 |
| Дано: ВС – дотична, О – центр кола, АВ = АС. Довести: ОВ = ОС |
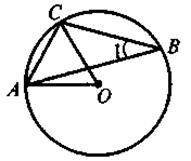
2 |
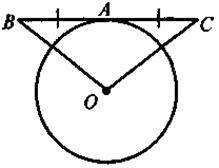
| Дано: О – центр кола, Знайти: кут 2 |
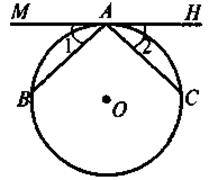
3 |
| Дано: МН – дотична, Довести: АВ = АС |
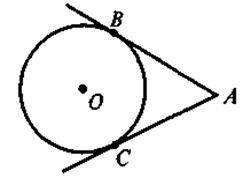
4 |
| Дано: О – центр кола, АВ і АС – дотичні. Довести: АВ = АС |
5 |
| Дано: О – центр кола, Довести: ?АОС – рівносторонній |
V. Засвоєння знань
План вивчення матеріалу
1. Означення чотирикутника, вписаного в коло.
2. Теорема про вписаний чотирикутник.
3. Наслідки з теореми про вписаний чотирикутник.
4. Означення описаною чотирикутника.
5. Теорема про описаний чотирикутник.
6. Наслідки з теореми про описаний чотирикутник.
@ За новою програмою і математики для дванадцятирічної школи учні мають не тільки оволодіти змістом та вміти застосовувати в розв’язуванні задач означення та теореми про вписаний і описаний чотирикутники, а й доводити ці теореми. Але, з огляду на достатньо високий рівень складності доведення теорем, що виражають ознаки вписаного й описаного чотирикутників (у підручнику цей факт зафіксовано за допомогою відповідного умовного позначення), вимагати від учнів відтворення доведення названих ознак автор вважає за недоцільне. Під час формування знань учнів (за наведеним вище планом) учителю слід приділю и увагу таким моментам:
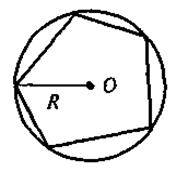
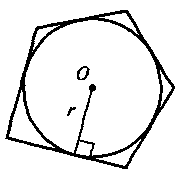
– під час вивчення означень вписаного (описаного) чотирикутника робимо акцент на тому, що тільки у випадку, коли всі вершини (сторони) чотирикутника лежать на колі (дотикаються до кола), даний чотирикутник буде називатися вписаним у коло (описаним навколо кола): на цьому етапі доцільно обговорити з учнями властивості чотирикутників та їх елементів, що пов’язані з колом (вершини чотирикутника, вписаного в коло, рівновіддалені від центра кола; відрізок, що з’єднує центр кола з будь-якою вершиною, є радіусом кола; для чотирикутника, описаною навколо кола, рівновіддаленими від центра кола будуть сторони, тобто перпендикуляр, проведений із центра кола, вписаного в чотирикутник, до сторони чотирикутника, і є радіусом цього кола); для закріплення цих фактів пропонується виконати завдання.
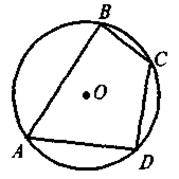
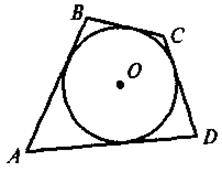
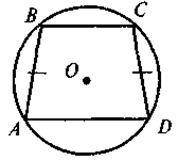
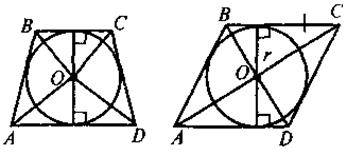
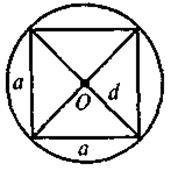
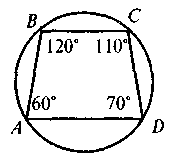
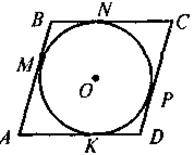
Завдання. На якому із наведених рисунків зображено чотирикутник ABCD:
А) вписаний у коло;
Б) описаний навколо кола?
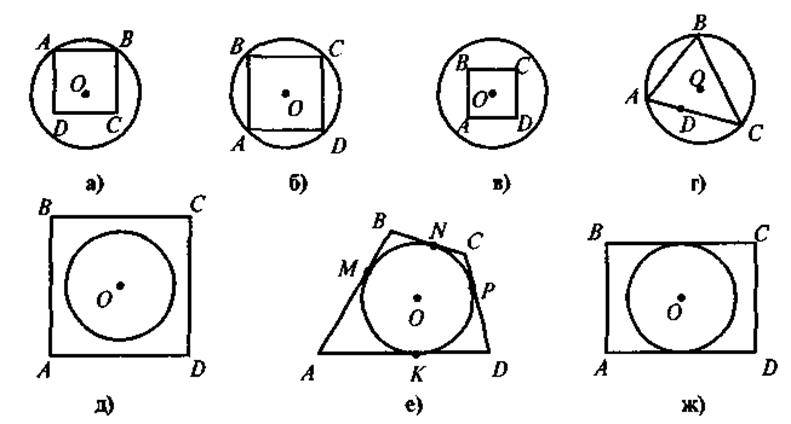
Для таких чотирикутників назвіть радіуси кіл(описаного або вписаного).
– Вивчивши зміст теорем (які виражають, по суті, критерії вписаного та описаного трикутників, тобто необхідну та достатню умови) про вписаний (описаний) чотирикутник, слід звернути увагу учнів на те, що можливі два випади їх застосування: по-перше, для визначення того, чи можна даний чотирикутник вписати в коло (описати навколо кола); по-друге, щоб записати відповідне співвідношення для протилежних кутів (сум протилежних сторін) чотирикутника. З метою закріплення цих тверджень учні розв’язують усні вправи.
Виконання усних вправ
1. У який прямокутник можна вписати коло? Навколо якого ромба можна описати коло?
2. Чи можна описати коло навколо чотирикутника, який має лише один прямий кут; лише три прямі кути?
– Для практичних потреб найбільшу цінність мають наслідки з теорем про вписаний та описаний чотирикутники, а також опорні задачі.
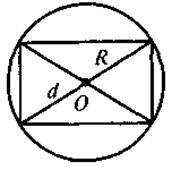
Задача 1. Центр кола, описаного навколо прямокутника, є точкою перетину його діагоналей.
Задача 2. Центр кола, вписаного в ромб, є точкою перетину його діагоналей, а радіус кола дорівнює половині висоти ромба.
Задача 3. Радіус кола, вписаного в трапецію, дорівнює половині її висоти.
Отже, після визначення видів чотирикутників, які можна вписати або описати, необхідно розглянути питання про положення центра описаного (вписаного) кола та співвідношення між елементами (сторонами, висотами) чотирикутників та радіусом описаного (вписаного) кола. Відповідні записи учні повинні зробити в зошитах.
Конспект 10 | |
Вписаний і описаний многокутники (вписане і описане кола) | |
|
|
Вписаний – усі вершини лежать на колі | Описаний – усі сторони є дотичними до кола.
Де Р – периметр, r – радіус вписаного кола |
Вписаний та описаний чотирикутники | |
|
|
І навпаки: якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло | AB + CD = BC + AD (суми довжин протилежних сторін рівні) І навпаки: якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло |
Прямокутник | |
|
1. Якщо паралелограм вписано в коло, то він прямокутник. 2. Центр кола, описаного навколо прямокутника, – точка перетину діагоналей |
Трапеція і ромб | |
|
|
Якщо ABCD – вписана трапеція, то AB = CD | D впиc. кола = h O – точка перетину бісектрис внутрішніх кутів.
|
Квадрат | |
|
|
|
|
VI. Формування первинних умінь
Виконання усних вправ
1. Чи можна описати коло навколо прямокутної трапеції?
2. У трапеції три сторони рівні. Чи можна в таку трапецію вписати коло? Чи можна навколо такої трапеції описати коло?
Виконання письмових вправ
1. Визначте, чи можна описати коло навколо чотирикутника ABCD, якщо кути А, В, С, D дорівнюють відповідно:
А) 90°, 90°, 20°, 160°; б) 5°, 120°, 175°, 60°.
2. Знайдіть невідомі кути:
А) вписаного чотирикутника, якщо два з них дорівнюють 46° і 125°;
Б) вписаної трапеції, якщо один із них дорівнює 80°;
В) вписаного чотирикутника, діагоналі якого точкою перетину діляться навпіл.
3. Знайдіть периметр:
А) описаного чотирикутника, три послідовні сторони якого дорівнюють 7 см, 9 см і 8 см;
Б) описаної трапеції, бічні сторони якої дорівнюють 3 см і 11 см.
4. Рівнобедрена трапеція описана навколо кола. Знайдіть середню лінію трапеції, якщо її бічна сторона дорівнює 7 см.
5. Діагональ ромба, що виходить з вершини кута 60°, дорівнює 24 см. Знайдіть радіус кола, вписаного в ромб.
VII. Підсумки уроку
Засвоєння учнями змісту основних тверджень перевіряємо під час Виконання завдання.
Які помилки допущено в зображенні чотирикутників (див. рис)?
А) | Б) АВ = 5 см, ВС = 5,5 см |
|
|
В) О – центр кола; ABCD – трапеція | Г) |
|
|
VIII. Домашнє завдання
Вивчити зміст теоретичного матеріалу. Виконати домашню самостійну роботу.
Домашня самостійна робота
1. У трикутнику ABC точки М і N – середини сторін АВ і ВС відповідно. Периметр трикутника ABC дорівнює 22 см. Знайдіть периметр трикутника MBN.
2. На рисунку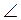 
ABB1 + 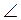A1AB = 180°. Знайдіть периметр чотирикутника АВВ1А1.
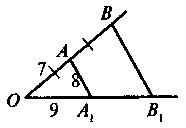
3. Знайдіть кути рівнобедреного трикутника, основа якого стягує п’яту частину дуги описаного кола. Розгляньте всі можливі випадки.
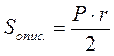(1 votes, average: 5.00 out of 5)
Loading...