Вправи 375-424
375.
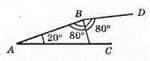
ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС.
376.
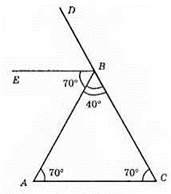
∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = (180° – 40°) : 2 = 140° : 2 = 70°. ∠EBA i ∠BAC – внутрішні різносторонні кути при прямих BE і АС і січній АВ. Отже, BE || АС.
377. Усередині трикутника побудовано найменшу кількість відрізків: 3. Поза трикутником: 2.
378.
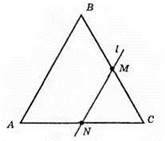
Якби
379.
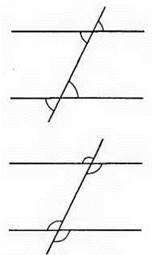
Знайдуться обов’язково:
А) рівно чотири гострі кути;
Б) не більш ніж чотири гострі кути;
В) не менш ніж чотири тупі кути;
Г) не менш ніж чотири рівні кути.
380.
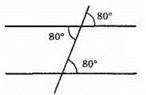
А) Ці кути можуть бути внутрішніми різносторонніми;
Б) не можуть бути внутрішніми односторонніми;
В) відповідними можуть бути.
381. 50° не може дорівнювати; 120° + 50° ≠ 180°.
382. ∠1 + ∠2 = 180°;
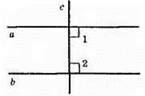
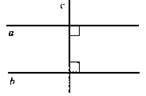
∠1 = ∠2 = 180° : 2 = 90°. с ⊥ а, с ⊥ b.
383.
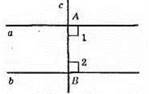
А || b; AB ⊥ a; AB ⊥ b; c – січна;
∠1 = ∠2 = 90°.
384. а)
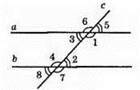
A || b; ∠1 + ∠2 = 180°; ∠3 + ∠4 = 180°; ∠5 + ∠1 = 180°; ∠5 + ∠6 = 180°; ∠6 + ∠3 = 180°; ∠7 + ∠2 = 180°; ∠7 + ∠8 = 180°; ∠8 + ∠4 = 180°.
Б)
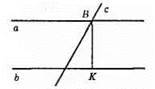
A || b; BK – відстань між a i b. BK ⊥ b.
385.
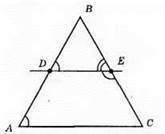
Б) DE || AC; ∠BDE = ∠BAC;
В) ∠DEC + ∠DEB = 180°.
386. a)
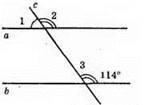
A || b, ∠2 = 114°; ∠2 = ∠3 (відповідні кути);
∠1 + ∠2 = 180° (суміжні кути);
∠1 = 180° – ∠2 = 180° – 114° = 66°.
Б)
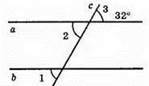
A || b; ∠2 = ∠3 = 32° (вертикальні кути);
∠1 = ∠2 = 32° (відповідні кути).
387.
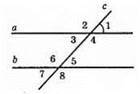
∠1 = 18°; ∠1 = ∠3 = 18° (вертикальні кути); ∠2 і ∠1 – суміжні кути;
∠2 = 180° – ∠1 = 180° – 18° – 162°;
∠4 = ∠2 – вертикальні кути;
∠5 = ∠1 = 18° – відповідні кути.
∠8 = ∠4 = 162° (відповідні кути);
∠7 = ∠5 = 18° (вертикальні кути);
∠6 = ∠8 = 162° (вертикальні кути).
388. a)
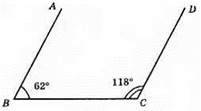
∠ABC = 62°; ∠BCD = 118°; AB || СD;
Б)
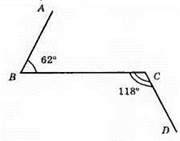
AD і CD перетинаються.
389.
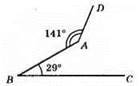
AD і BC не можуть бути паралельними.
390. a || b, a ⊥ c, b ⊥ c.
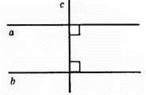
391.
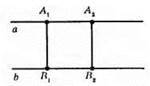
A || b, A1A2 і B1B2 – відстані між прямими A1B! і A2B2.
392. a)
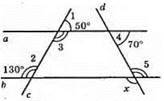
∠1 + ∠3 = 180° (суміжні кути);
∠3 = 180° – 50° = 130°; ∠3 = ∠2 = 130°; ∠3 і ∠2 – внутрішні різносторонні кути. Отже, a || b. ∠4 + ∠5 = 180° (внутрішні односторонні кути). ∠5 = 180° – 70° = 110°; ∠x = ∠5 = 110° (вертикальні кути).
Б)
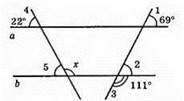
А і b – прямі, ∠2 + ∠3 = 180° (суміжні кути); ∠2 = 180° – 111° = 69°; ∠1 = ∠2 = 69° (відповідні кути).
Отже, a || b.
∠4 = ∠5 = 22° (відповідні кути).
∠x + ∠5 = 180° (суміжні кути).
∠x = 180° – 22° = 158°.
393. a)
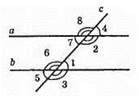
∠1 і ∠2 – внутрішні односторонні кути;
∠1 = х, ∠2 = х + 30°; х + х + 30° = 180°; 2х = 180° – 30°; 2х = 150°; x = 75°;
∠1 = 75°; ∠2 = 105°.
∠1 = ∠4 = 75° (відповідні кути);
∠3 = ∠2 = 105° (відповідні кути).
∠1 = ∠5 = 75° (вертикальні кути);
∠3 = ∠6 = 105° (вертикальні кути);
∠7 = ∠4 = 75° (вертикальні кути);
∠2 = ∠8 = 105° (вертикальні кути).
Б)
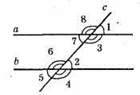
∠1 + ∠2 = 56°; ∠1 = ∠2 = 28° (відповідні кути);
∠3 = ∠4 = 180° – 28° = 152° (суміжні кути);
∠5 = ∠2 (вертикальні кути);
∠5 = 28°; ∠6 = ∠4 = 152° (вертикальні кути);
∠7 = ∠1 = 28° (вертикальні кути);
∠3 = ∠8 = 152° (вертикальні кути).
394.
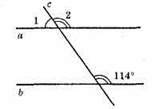
∠2 – ∠1 = 54°. Hexaй ∠1 = х, тоді ∠2 = х + 54°; х + х + 54° = 180°; ∠1 і ∠2 – суміжні кути; 2х + 54° = 180°; 2х = 180° – 54°; 2х = 126°; x = 63°; ∠1 = 63°; ∠2 = 54° + 63° = 117°. Прямі а і bнепаралельні.
395.
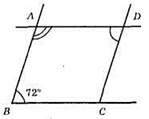
AD || ВС; AB – січна; CD || AB; AD – січна; ∠A + ∠B = 180°; ∠A = 180° – 72° = 108°; ∠A + ∠D = 180°; ∠D = 180° – 108° = 72°; ∠D = 72°.
396. AD || DC; DD – січна; ∠1 = ∠2;
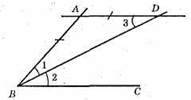
BD – бісектриса; ∠2 = ∠3 – внутрішні різносторонні кути; ∠1 = ∠2 (за умовою) ⇒ ∠2 = ∠3, отже, ∠1 = ∠3, тобто? ABD – рівнобедрений.
397.
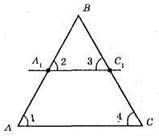
?АВС; AB = CD; A1C1 || АС; ?А1ВС1- рівнобедрений, A1B = C1B; ∠1 = ∠2 (відповідні), АС || A1C1, AB – січна; ∠3 = ∠4 (відповідні), A1C1 || АС, BC – січна; ∠1 = ∠4, ∠2 = ∠3.
398.
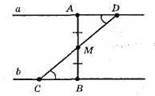
AB ⊥ а; AB ⊥ b; M – середина AB; AM = BM.
?MAD = ?MBC; ∠D = ∠C – внутрішні різносторонні кути а || b, CD – січна; ∠A = ∠B = 90°; AM = BM; ∠AMD = ∠BMC = 90°; ?AMD = ?BMC, з їхньої рівності маємо: CM = DM.
399.
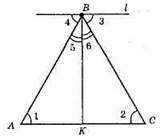
L || AC; AB = CB; BK – медіана? АВС; BK – медіана, висота рівнобедреного трикутника, BK ⊥ AC; ∠3 = ∠2, ∠1 = ∠4 – внутрішні різносторонні кути.
∠5 = ∠6, BK – бісектриса кута.
∠4 + ∠5 + ∠6 + ∠3 = 180°; ∠4 + ∠5 = ∠6 + ∠3 = 90°; BK ⊥ l. BK – відстань між прямими l і AC.
400. a)
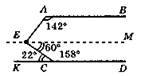
EM || KD. ∠KCE і ∠ECD – суміжні кути; ∠KCE = 180° – 158° = 22°; ∠ECK = ∠MEC = 22°; ∠AEM = 60° – 22° = 38°; ∠MEA + ∠EABM = 38° + 142° = 180°; ∠MEA і ∠EAB – внутрішні односторонні кути; EM || AB; CD || EM, EM || AB, отже, CD || AB.
Б)
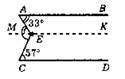
MK || CD; ∠MEC = ∠ECD = 57° – внутрішні різносторонні кути, ∠AEM = 100° – 57° = 43°. ∠MEA ≠ ∠EAB. Прямі EK і AB непаралельні, CD не паралельна AB.
401.
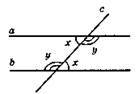
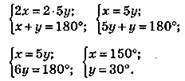
Відповідь: 30°, 150°.
А) Всі кути 90°;
В) 50°, 130°.
402.
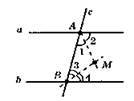
А || b, с – січна. ∠A + ∠B = 180°; ∠1 = ∠2, ∠3 = ∠4, AM і BM – бісектриси кутів;
∠1 + ∠2 + ∠3 + ∠4 = 180°; ∠1 + ∠3 = 90°.
?ABM; ∠AMB = 90°; ∠1 + ∠3 = 90°; ∠AMB = 180° – 90° = 90°, отже, AM ⊥ BM.
403.
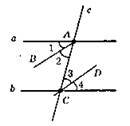
A || b, c – січна; AB і CD – бісектриси внутрішніх різносторонніх кутів; ∠1 = ∠2; ∠3 = ∠4; ∠A = ∠C; a || b, c – січна; ∠2 = ∠3 – це внутрішні різносторонні кути при прямих AB і CD і січній АС, отже, AB || CD.
404.
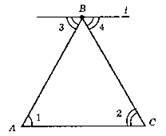
L || АС; ∠3 = ∠1, кути внутрішні різносторонні при прямих l і АС, AB – січна; ∠2 = ∠4, кути внутрішні різносторонні при прямих l і АС, ВС – січна. AB + ВС = ВС + АС = AB + АС. Якщо у трикутнику всі сторони рівні, то в ньому всі кути рівні, ∠A = ∠B = ∠C.
405.
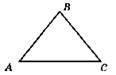
AB + ВС = ВС + АС ⇒ АВ = АС; ВС + АС = AB + АС ⇒ ВС = AB, отже, AB = АС, АВ = ВС = АС = ВС, тобто AB = АС = ВС.
406. Три тупих кути – ні. Два тупих кути – ні. Жодного тупого кута – так.
407. При основі рівнобедреного трикутника кут не може бути тупим, прямим.
408. Прямокутний трикутник може бути рівнобедреним.
Прямокутний трикутник не може бути рівностороннім.
409. Ні.
410.
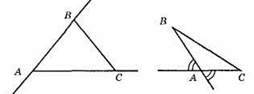
Гострими кутами можуть бути кути тільки при одній вершині.
411. ∠A + ∠B + ∠C = 180.
А) 180°;
Б) ∠BCD = 180° – 40° = 140°.
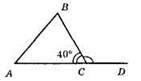
В) Прямокутний, гострокутний, тупокутний.
412.
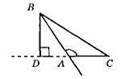
А) BD ⊥ АС; AABD – прямокутний;
Б) ∠BAD – суміжний ∠BAC.
413. а) 65° і 45°; 180° – 65° – 45° = 70°
Б) 120° і 18°; 180° – 120° – 18° = 42°;
В) 90° і 64°; 180° – 90° – 64° = 26°.
414. а)
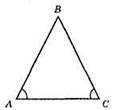
AB = BC; ∠A = ∠C = 40°;
∠B = 180° – (40° + 40°) = 180° – 80° = 100°;
Б)
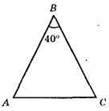
?АВС; АВ = СВ;
∠A = ∠C = (180° – 40°) : 2 = 140° : 2 = 70°.
415. а)
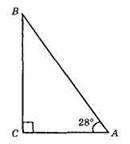
∠B = 180° – 90° – 28° = 90° – 28° = 62°;
Б)
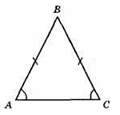
∠A = ∠C = 80°;
∠B = 180°- (80° + 80°) = 180° – 160° = 20°.
416. Якщо кут при основі рівнобедреного трикутника тупий, то сума кутів трикутника більше 180°.
417. Якщо в трикутнику більше, ніж один прямий кут, то сума кутів трикутника більше 180°.
418.
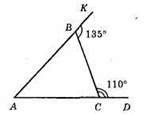
1) ∠ABC = 180° – 135° = 45°;
2) ∠BCA = 180° – 110° = 70°;
3) ∠BAC = 180° – 45° – 70° = 65°.
Відповідь: 45°, 70°, 65°.
419. 1) BCF – 180° – 40° = 140°;
2) ∠BAC = 180° – 125° = 55°;
3) ∠ABC = 180° – (55° + 40°) = 180° – 95° = 85°;
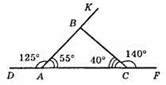
4) ∠KBC = 180° – 85° = 95°.
420.
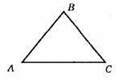
А) Нехай один кут х, другий кут 2х, а третій кут (х – 20°). ∠A = х, ∠B = 2х, ∠C = х – 20°.
Рівняння: х + 2х + х – 20° = 180°; 4х = 200°; х = 200° : 4; х = 50°; ∠A = 50°, ∠B = 100°, ∠C = 30°.
Відповідь: 50°, 100°, 30°.
Б) ∠A : ∠B : ∠C = 1 : 3 : 5. Нехай спільна міра кутів х, тоді ∠A = х, ∠B = 3х, ∠C = 5х.
Х + 3х + 5х = 180°; 9х = 180°; х = 180° : 9; х = 20°; ∠A = 20°; ∠B = 60°; ∠C = 100°.
Відповідь: 20°, 60°, 100°.
421.
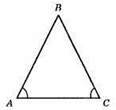
Нехай AB = ВС, тоді ∠A = ∠C = 50°; ∠B = 180° – (50° + 50°) = 180° – 100° = 80°. Якщо ∠B = 50°, TO ∠A = ∠C = (180° – 50°) : 2 = 130° : 2 = 65°.
Відповідь: 50°, 50°, 80° або 50°, 65°, 65°.
422. а) ∠A : ∠B : ∠C = 2 : 7 : 9. ∠A = 2х, ∠B = 7x; ∠C = 9x.
2х + 7х + 9х = 180°; 18х = 180°; х = 180° : 18; х = 10°. ∠A = 20°, ∠B = 70°, ∠C = 90°.
Б)
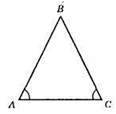
AB = СD, ∠B = 100°; ∠A = ∠C = (180° – 100°) : 2 = 80° : 2 = 40°.
Відповідь: 100°, 40°, 40°.
423.
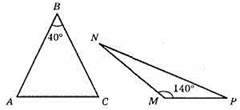
Відповідь: ні, не може.
424.
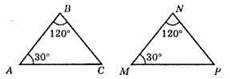
?ABC = ?MNP; ∠A = ∠M; ∠B = ∠N; ∠C = ∠P.
∠B = ∠N = 120°; ∠M = ∠A = 30°;
∠A = ∠C= 30°; ∠M = ∠P = 30°;
∠C = ∠P = 180° – (120° + 30°) = 30°;
?ABC і? MNP – рівнобедрені.