Застосування властивостей показникової функції до розв’язування вправ
УРОК 44
Тема. Застосування властивостей показникової функції до розв’язування вправ
Мета уроку. Формування умінь учнів застосовувати властивості показникової функції до розв’язування вправ. Познайомити учнів з використанням показникової функції під час вивчення явищ навколишнього середовища.
І. Перевірка домашнього завдання
Колективне обговорення № 1-12 із “Запитання і завдання для повторення” § 1 розділу IV.
II. Набуття умінь застосовувати властивості показникової функції до розв’язування вправ
Початковий
1. Знайдіть значення функції у = 3х, якщо: а) х = 2; б) х = – 2; в) х = 0.
Відповідь: а) 9; б) 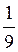 ; в) 1.
; в) 1.
2. На якому з рисунків (рис. 144) подано графік функції: a) y =5х; б) 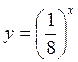 ?
?
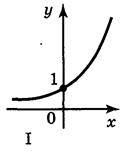
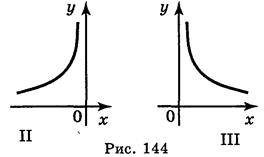
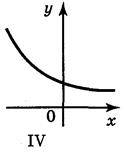
Відповідь: а) І; б) IV.
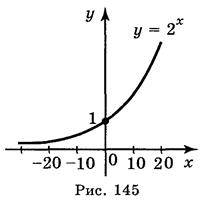
3. Користуючись графіком функції у = 2х, порівняйте значення виразів (рис. 145): а) 210 і 220; б) 2-10 і 210; в) 2-10 і 2-20.
Відповідь: а) 210 < 220; б) 2-10 < 210; в) 2-10 > 2-20.
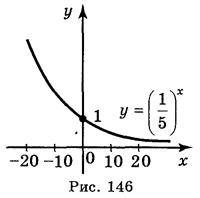
4. Користуючись графіком функції 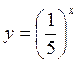 , порівняйте значення виразів (рис. 146): a)
, порівняйте значення виразів (рис. 146): a) 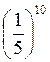
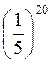 ; б)
; б) 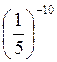 І
І 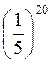 ; в)
; в) 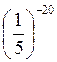 І
І 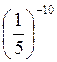 .
.Відповідь: a) 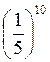 >
> 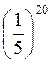 ; б)
; б) 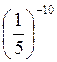 >
> 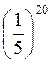 ; в)
; в) 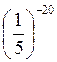 >
> 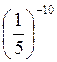 .
.
Середній рівень
1. Знайдіть область визначення функцій: а) y = 2x + 6; б) 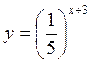 ; в) y = 3x + 1; г)
; в) y = 3x + 1; г) 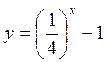 .
.
Відповідь: a) R; б) R; в) R; г) R.
2. Побудуйте схематично графік функцій:
A) y = 1,7x; б) 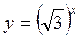 ; в) y = 0,3х; г)
; в) y = 0,3х; г) 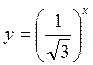 .
.
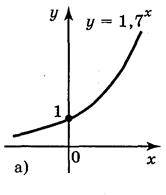
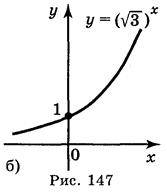
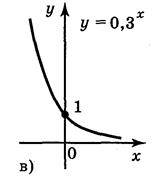
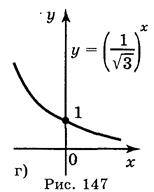
Відповідь: рис. 147: а); б); в); г).
3. Порівняйте числа: а) 1,83 і 1; б) 0,85 і 1; в) 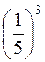 і 5-4; г)
і 5-4; г) 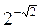 і
і 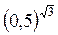 .
.
Відповідь: а) 1,83 > 1; б) 0,85 < 1; в) 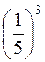 > 5-4; г)
> 5-4; г) 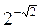 >
>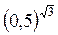 .
.
4. Порівняйте числа х і у, якщо відомо, що вірна нерівність:
А) 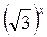 <
< 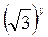 ; б)
; б) 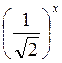 <
< 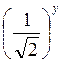 ; в) 3х <
; в) 3х < 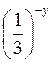 ; г)
; г) 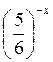 <
<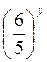 .
.
Відповідь: а) х < у; б) х > у; в) х < у; г) х < у.
5. Порівняйте основу a > 0 з одиницею, якщо відомо, що вірна нерівність:
А) а-2 > а2; б) аn > а3; в) 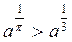 ; г)
; г) 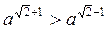 .
.
Відповідь: а) 0 < a < 1; б) а > 1; в) 0 < а < 1; г) а > 1.
Достатній рівень
1. Знайдіть область визначення функцій: а) 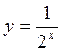 ; б) y=
; б) y=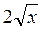 ; в)
; в) 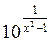 .
.
Відповідь: а) R; б) [0; + ); в) (-
); в) (- ; -1)
; -1) 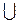 (-1; 1)
(-1; 1) 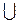 (1; +
(1; + ).
).
2. Побудуйте графіки функцій: a) y =3x + 1; б) 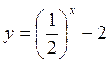 ; в) y = nх – 2; г) y = 3х+1.
; в) y = nх – 2; г) y = 3х+1.
Відповідь: (рис. 148) а); б); в); г).
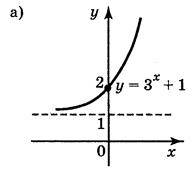
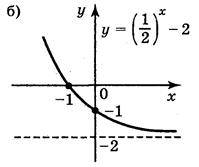
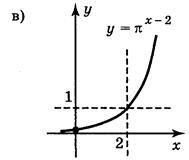
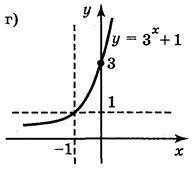
Рис. 148
3. Знайдіть множину значень функцій:
А) у = -3х; б) 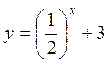 ; в)
; в) 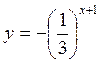 ; г) y = 5х – 3.
; г) y = 5х – 3.
Відповідь: а) (- ; 0); б) (3; +
; 0); б) (3; + ); в) (-
); в) (- ; 0); г) (-3; +
; 0); г) (-3; + ).
).
4. Який висновок можна зробити відносно показника х, якщо:
А) 5х = 10; б) 5х = 3; в) 0,01х = 2; г) 100х = 2.
Відповідь: а) х > 1; б) 0 < х < 1; в) 0 < х < 1; г) 0 < х < 1.
Високий рівень
1. Знайдіть область визначення функцій:
А) 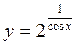 ; б)
; б) 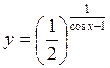 ; в)
; в) 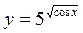 ; г)
; г) 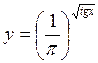 .
.
Відповідь: а) х?  + ?n, n
+ ?n, n Z; б) х?
Z; б) х?  + 2?n, n
+ 2?n, n Z;
Z;
В) –  + 2?n
+ 2?n 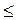 х
х 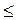
 + 2?n, n
+ 2?n, n Z; г) ?n
Z; г) ?n 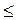 х <
х <  + ?n, n
+ ?n, n Z.
Z.
2. Побудуйте графіки функцій:
A) у =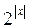 ; б) у =
; б) у = 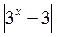 ; в)
; в) 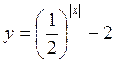 ; г)
; г) 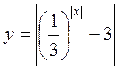 .
.
Відповідь: (рис. 149) а); б); в); г).

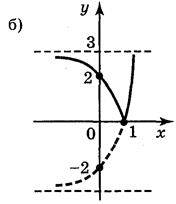
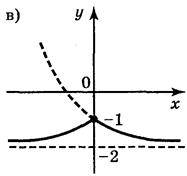
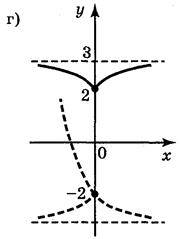
Рис. 149
3. Знайдіть найбільше і найменше значення функції:
А) 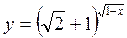 ; б)
; б) 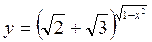 ; в) y = nsinx; г)
; в) y = nsinx; г) 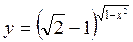 .
.
Відповідь: а) найбільшого немає, найменше 1; б) найбільше 2, найменше 1; в) найбільше n, найменше 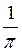 ; г) найбільше 1, найменше
; г) найбільше 1, найменше  – 1.
– 1.
III. Сприймання і усвідомлення нового матеріалу
Показникова функція часто використовується для описання різних процесів у природі і техніці.
Так, радіоактивний розпад виражається формулою 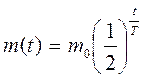
Де m(t) – маса радіоактивної речовини в момент часу t;
Т0 – маса радіоактивної речовини в момент часу t = 0;
Т – період напіврозпаду (проміжок часу, за який початкова кількість речовини зменшується удвічі).
За допомогою показникової функції виражається тиск повітря в залежності від висоти підйому, приріст деревини, кількість бактерій, які розмножуються в деякому середовищі тощо.
Більш детальніше про практичне використання показникової функції ви прочитаєте в підручнику. А зараз розв’яжемо задачу.
При радіоактивному розпаді кількість речовини зменшується вдвічі за добу. Скільки речовини залишиться від 250 г через: а) 1,5 доби; б) 3,5 доби?
За умовою задачі т0 = 250 г, Т = 1 доба. За законом радіоактивного розпаду маємо:
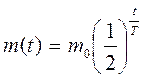 ,
, 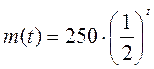 .
.
Знайдемо m(1,5) і m(3,5):
А) 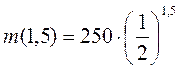 = 250 – (0,5)1,5
= 250 – (0,5)1,5 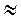 88,4 (г);
88,4 (г);
Б) 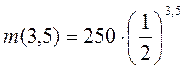 = 250 – (0,5)3,5
= 250 – (0,5)3,5 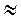 22,1 (г).
22,1 (г).
IV. Підсумок уроку
V. Домашнє завдання
Розділ IV § 1. “Запитання і завдання для повторення” № 13-16, 25.