Головна ⇒ 📌Формули й таблиці ⇒ Значення функцій деяких кутів – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Значення функцій деяких кутів – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Формули й таблиці
МАТЕМАТИКА
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Значення функцій деяких кутів α
0; 2π | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | |
0; 360° | 30° | 45° | 60° | 90° | 180° | 270° | |
Sin α | 0 | 1/2 |
|
| 1 | 0 | -1 |
Cos α | 1 |
|
| 1/2 | 0 | -1 | 0 |
Tg α | 0 | 1/ | 1 |
| Не існують | 0 | Не існують |
Ctg α | Не існують |
| 1 | 1/ | 0 | Не існують | 0 |
Sin(-α) = – sin α | Cos(-α) = cos α | Tg(-α) = – tg α | Ctg(-α) = – ctg α |
Related posts:
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Урок № 58 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Мета: закріпити знання учнями змісту формул доповнення та числових значень тригонометричних функцій кутів 30°, 45°, 60°. Сформувати вміння застосовувати формули до розв’язування задач. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: конспект 22. Хід уроку I. Організаційний етап […]...
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...
- Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
- Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Тригонометричні функції числового аргументу Математика – Алгебра Тригонометричні функції Тригонометричні функції числового аргументу Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці і радіус якого дорівнює 1 (див. рисунок). Нехай точка P0 – це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним – проти. […]...
- Показникова функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Показникова функція У = ах (0 < а < 1) У = ах (а > 1) Область визначення Х (-∞;+∞) Х (-∞;+∞) Множина значень Y (0;+∞) Y (0;+∞) Перетин з віссю Y При х = 0, y = 1. При х = 0, y = 1. Монотонність Функція спадає […]...
- Логарифмічна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Логарифмічна функція Y = logax(0 < a < 1) У = logax(а > 1) Область визначення Х (0;+∞) Х (0;+∞) Множина значень Y (-∞;+∞) Y (-∞;+∞) Перетин з осями координат З віссю ОХ Х = 1, у = 0; Х = 1, у = 0; З віссю OY Перетину […]...
- Тригонометричні функції кута УРОК 5 Тема. Тригонометричні функції кута Мета уроку: повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута. І. Аналіз помилок, допущених у математичному диктанті та самостійній роботі. 1. Побудуйте графіки функцій (індивідуальні картки): А) ; б) ; в) ; г) . Відповідь: а) рис. 25; б) рис. 26; в) […]...
- Основні тригонометричні тотожності – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні тотожності...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції з раціональними показниками...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Значення синусів і косинусів окремих кутів 10. Додатки 33. Значення синусів і косинусів окремих кутів...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Тригонометричні функції числового аргументу УРОК 7 Тема. Тригонометричні функції числового аргументу Мета уроку: Формування поняття тригонометричних функцій числового аргументу; вивчення значень тригонометричних функцій деяких чисел (кутів), зміни знаків тригонометричних функцій у координатних чвертях. І. Перевірка домашнього завдання Розв’язування вправ аналогічних до домашніх. 1. Подайте в радіанній мірі кути: А) 5°; б) 1140°; в) -765°; г) 67° 5′. Відповідь: а) […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
- Лінійні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Лінійні функції...
- Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....
- Основні тригонометричні рівняння – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні рівняння Sin x = 0 X = πk, k Z Cos x = 0 X = π/2 + 2πk, k Z Sin x = 1 X = π/2 + 2πk, k Z Cos x = 1 X = 2πk, k Z Sin x = -1 X […]...
- Квадратичні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Квадратичні функції Графіком квадратичної функції є парабола, яка отримується з графіка функції у = ах2 за допомогою двох паралельних перенесень: – перенесення уздовж осі ОХ на m одиниць ліворуч, якщо m < 0, і праворуч, якщо m > 0; – перенесення уздовж осі OY на у0 одиниць […]...
- Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 54 Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації Мета: – формувати теоретичну базу знань учнів з теми, спираючись на міжпредметні зв’язки; – розвивати практичні вміння та навички щодо опрацювання табличної інформації за допомогою формул та вбудованих […]...
- Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій УРОК 3 Тема. Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій Мета уроку: Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = […]...
- Радіанна система вимірювання кутів і дуг Математика – Алгебра Тригонометричні функції Радіанна система вимірювання кутів і дуг 1 радіан – це такий центральний кут, для якого довжина відповідної дуги дорівнює довжині радіуса. Формули переходу: від радіанної міри до градусної: ; від градусної до радіанної: , де – градусна міра деякого кута, a – його радіанна міра. Корисно пам’ятати: 2π – 360°, […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
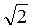 /2
/2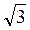 /2
/2