Числові послідовності
УРОК № 65
Тема. Числові послідовності
Тестові завдання
1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3.
А) 3; б) 17; в) 5; г) інша відповідь.
2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3.
А) 1536; б) 18; в) 21; г) інша відповідь.
3. Знайдіть суму перших п’яти членів арифметичної прогресії (bn), якщо b1 = – 10, а різниця дорівнює 10.
А) 0; б) 50; в) 100; г) -100.
4. Чому може дорівнювати знаменник геометричної прогресії (bn), якщо b10 = 10; b12 = 40?
А) 2; б) ±2; в) 4; г) 15.
5. Чому дорівнює сума п’яти перших членів геометричної
А) 11; б) -17; в) 17; г) інша відповідь.
6. Знайдіть суму нескінченної геометричної прогресії (аn), якщо а1 = 3, а2 = 0,3.
А) 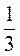 ; б) 3
; б) 3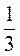 ; в) -3
; в) -3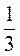 ; г) 1.
; г) 1.
Письмові вправи
1. Знайдіть різницю арифметичної прогресії, перший член якої дорівнює 10, а сума перших 14-ти членів дорівнює 1050.
2. Знайдіть суму перших шести членів геометричної прогресії (bn), якщо b2 = 12, b5 = -96.
3. Послідовність задано формулою хn = n2 – 3n + 1. Знайдіть номер члена цієї послідовності, якщо він дорівнює 19.
4. Запишіть у вигляді звичайного нескоротного дробу число 0,3(2).
5. При якому значенні х числа 3х – 1; х + 5 і x + 17 будуть послідовними членами геометричної прогресії?
6. Знайдіть суму всіх трицифрових чисел, менших за 250, що кратні 3.
Related posts:
- Сума перших n членів геометричної прогресії УРОК № 57 Тема. Сума перших n членів геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед числових послідовностей, відшукувати знаменник геометричної прогресії, перші члени геометричної прогресії, а […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Геометрична прогресія. Формула n-го члена геометричної прогресії УРОК № 55 Тема. Геометрична прогресія. Формула n-го члена геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед інших числових послідовностей, відшукувати знаменник геометричної прогресії, перші кілька членів […]...
- Сума перших n членів арифметичної прогресії УРОК № 53 Тема. Сума перших n членів арифметичної прогресії Мета уроку: закріпити знання учнів про формули обчислення суми перших n членів арифметичної прогресії, а також про її означення та властивості, вивчені на попередніх уроках; сформувати уявлення про спосіб розв’язування задач на відшукання суми послідовних членів арифметичної прогресії з n-го по т-й включно (n < […]...
- Геометрична прогресія УРОК № 54 Тема. Геометрична прогресія Мета уроку: домогтися засвоєння учнями: означення геометричної прогресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивостей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули […]...
- Арифметична прогресія. Формула n-го члена арифметичної прогресії УРОК № 51 Тема. Арифметична прогресія. Формула n – го члена арифметичної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять арифметичної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена арифметичної прогресії. Закріпити вміння: вирізняти арифметичну прогресію серед числових послідовностей, відшукувати різницю арифметичної прогресії, перші члени […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Числові і буквені вирази. Формули. Властивості додавання і віднімання УРОК 26 Тема. Числові і буквені вирази. Формули. Властивості додавання і віднімання Мета: закріпити знання учнів про основні поняття теми (числові і буквені вирази, формули, значення числового виразу); продовжувати відпрацьовувати навички складання і знаходження значень буквених виразів при зазначених значеннях змінних, повторити тему “Додавання і віднімання”; підготовити учнів до тематичної контрольної роботи № 2. Тип […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Числові функції. Зростаючі і спадні, парні і непарні функції УРОК 1 Тема. Числові функції. Зростаючі і спадні, парні і непарні функції Мета уроку: Узагальнення і систематизація знань учнів про числові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції). І. Мотивація навчання Процеси реального світу тісно пов’язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв’язок […]...
- Числові і буквені вирази. Формули Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 9. Числові і буквені вирази. Формули Як знайти периметр прямокутника, сторони якого дорівнюють 3 см і 5 см (рис. 70)? Рис. 70 Відповідаючи на це запитання, ви, скоріше за все, зробите такий запис: 2 ∙ 3 + 2 ∙ 5. […]...
- ЧИСЛОВІ ВИРАЗИ РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ У розділі дізнаєтесь: · про числові вирази та їх види; · чим відрізняються числовий вираз і вираз зі змінними; · що таке допустимі значення змінних у виразі; · які вирази називають цілими; · як обчислювати значення виразу зі змінними; · про способи спрощення виразів; · яка рівність е тотожністю та […]...
- ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ Ви вже знаєте чотири арифметичні дії над числами – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 […]...
- Числові й буквені вирази Урок № 41. Тема. Числові й буквені вирази Мета уроку. Закріпити в учнів навики розв’язування вправ на спрощення та обчислення буквених виразів в знайомих і змінених ситуаціях. Розвивати здібності на основі розумових дій т а операцій. Виховувати вміння творчо працювати. Обладнання. Таблиця “Порядок дій”, дидактичні матеріали. Хід уроку І. Повідомити тему, мету уроку. ІІ. Перевірка […]...
- Квадратні рівняння Тестові завдання Тестове завдання № 4 . Квадратні рівняння 1. Яке з рівнянь є квадратним? А Б В Г 7х – 3 = 0 (х – 1)2 = х2 – 4х 5х2 = 4х2 2. Знайдіть коефіцієнти a, b і с квадратного рівняння 3 – х2 – 6х = 0. А Б В Г 3; […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Підсумкова контрольна робота з курсу математики за 5 клас Урок 126 Тема. Підсумкова контрольна робота з курсу математики за 5 клас Варіант 1 1°. Знайдіть значення виразу й округліть його до десятих: (4,1 – 0,66 : 1,2) – 0,6 + 0,125. 2°. Михайлик ішов з одного села в інше 0,7 год. полем і 0,9 год. через ліс, пройшовши 5,31 км. З якою швидкістю ішов […]...
- ЧИСЛОВІ МНОЖИНИ. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: повторити усну і письмову нумерацію чисел першої сотні; випадки додавання і віднімання в межах 20; розвивати мислення, пам’ять; виховувати акуратність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 153, завдання 984; 985) Завдання 984 Стає був у таборі з 15 липня по 7 серпня включно. Скільки днів був […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Вирази. Числові вирази Урок № 12 Тема. Вирази. Числові вирази Мета: систематизувати та узагальнити знання про числові й буквені вирази, набуті учнями в 5-6 класах. Тип уроку: систематизація та узагальнення знань. Хід уроку І. Аналіз тематичної контрольної роботи Про результати попереднього уроку (тематична контрольна робота № 1) учні дізнаються до уроку (учитель може роздати зошити із тематичної контрольної […]...
- СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Числові і буквені вирази. Формули УРОК 25 Тема. Числові і буквені вирази. Формули Мета: сформувати уявлення учнів про формули як ключ до розв’язання цілого класу задач; продовжувати формування вмінь учнів знаходити значення буквених виразів, а також читати їх і складати буквені вирази за умовою задачі. Тип уроку: засвоєння навичок та вмінь. Обладнання: таблиця-схема “Формули. Вирази”. Хід уроку І. Перевірка домашнього […]...
- Числові проміжки. Переріз і об’єднання проміжків УРОК № 10 Тема. Числові проміжки. Переріз і об’єднання проміжків Мета уроку: домогтися засвоєння учнями змісту понять: числовий проміжок, переріз та об’єднання числових проміжків, а також усвідомлення учнями існування різних видів числових проміжків, що відповідають різним видам нерівностей. Розпочати роботу з вироблення вмінь відтворювати зміст вивчених понять, записувати числові проміжки, що відповідають різним видам нерівностей […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Числові вирази. Буквені вирази та їх значення. Формули Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 10. Числові вирази. Буквені вирази та їх значення. Формули Приклад 1. Поїзд проїхав за першу годину 60 км, а за другу – на 5 км більше. Скільки кілометрів проїхав потяг за дві години? Розв’язання. За другу годину потяг проїхав 60 + 5 […]...
- Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об’єм УРОК 64 Тема. Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об’єм Мета: перевірити засвоєння практичних знань та вмінь учнів з вивчених тем. Тип уроку: перевірка й корекція знань, навичок і вмінь. Обладнання: таблиці “Ділення з остачею”, “Площа прямокутника”, “Об’єм прямокутного паралелепіпеда”. Хід уроку І. Тематична контрольна робота № 5 Варіант 1 1. Виконайте […]...