ЧИТАННЯ І ЗАПИС ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНАМИ І ЧАСТИНИ ВІД ЧИСЛА
Мета: ознайомити учнів з правилом запису будь-якого чотирицифрового числа; закріплювати вміння читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною; вдосконалювати навички усних і письмових обчислень, розв’язування задач двома способами; розвивати мислення; виховувати інтерес до предмета.
ХІД УРОКУ
I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
Завдання 183
– Прочитайте числа, в записі яких більше цифр, ніж доданків. Одиниці якого розряду відсутні в цих числах?
Завдання 184
– Прочитайте вираз, за допомогою якого розв’язали задачу.
(60 + 24) : k, якщо k = 12, то (60 + 24) : 12 = 7 (м)
III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
1. Усні обчислення
– Полічіть тисячами від 1000 до 10 000 і навпаки.
Робота в групах. “Хто швидше обчислить математичний ланцюжок?”
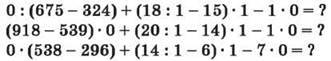
2. Математичний диктант
– Записати число, що складається з 85 десятків.
– Скільки сантиметрів у 4 м 2 см?
– Яке число стоїть між 998 і 1000?
– Скільки метрів у 900 см?
– Скільки всього копійок в 1 грн 4 к.?
–
– Різницю чисел 500 і 200 зменшити на 30.
– Суму чисел 25 і 75 зменшити в 4 рази.
– Добуток чисел 17 і 5 збільшити на 15.
3. Робота в групах
– Які знаки дій можна поставити замість  і які цифри – замість
і які цифри – замість  , щоб отримати правильні рівності?
, щоб отримати правильні рівності?
Кожна група отримує завдання. Перемагає група, яка правильно і швидко виконає завдання.

Відповіді:

IV. РОБОТА НАД НОВИМ МАТЕРІАЛОМ
1. Робота за підручником
Завдання 185
Учні називають пари чисел. Аналізують, що у них спільного і чим вони відрізняються.
Ознайомлення з правилом запису чотирицифрових чисел
– Прочитайте числа 7568; 4827:
7568 – це 7 тис. 568 (сім тисяч п’ятсот шістдесят вісім);
4827 – це 4 тис. 827 (чотири тисячі вісімсот двадцять сім).
– На основі складання різних форм представлення числа отримуємо правило запису будь-якого чотирицифрового числа: спочатку записують одиниці розряду тисяч, потім – сотень, десятків, одиниць.
Завдання 186 (з коментуванням)
2. Фізкультхвилинка
V. РОЗВИТОК МАТЕМАТИЧНИХ ЗНАНЬ
1. Знаходження частини числа і числа за його частиною
Практична робота (завдання 187)
Діти виконують завдання в парах, попередньо повторивши, як знайти частину числа і число за його частиною.
Завдання 188
– Щоб знайти частину числа, потрібно великі грошові одиниці перетворити на менші.

2. Робота над задачами
Завдання 189
Після роботи над текстом задачі учні аналізують її.
– Які колоди були на складі?
– Що зробили з сосновими колодами?
– Як знайти кількість розпиляних соснових колод?
Учні розв’язують задачу самостійно з подальшою взаємоперевіркою.
Розв’язання
1) 48 + 56 = 104 (к.) – було на складі;
2) 56 : 4 = 14 (к.) – соснових розпиляли;
3) 104 – 14 = 90 (к.) – залишилося на складі;
4) 90 – 14 = 76 (к.)
– Поясніть розв’язання задачі виразом.
48 + 56 – 56 : 4 – 56 : 4 = 76 (к.) – менше розпиляли, ніж залишилося.
Завдання 190
Діти розв’язують задачу самостійно з подальшою перевіркою, під час якої з’ясовують, яким способом вони розв’язували задачу. Коментують обидва способи розв’язання.
І спосіб
1) 4 + 3= 7 (кг) – фарби витратили для ремонту одного класу;
2) 7 • 12 = 84 (кг) – фарби потрібно для ремонту 12 класів;
(4 + 3) • 12 = 84 (кг)
ІІ спосіб
1) 4 • 12 = 48 (кг) – білої фарби знадобиться;
2) 3 • 12 = 36 (кг) – коричневої фарби потрібно;
3) 48 + 36 = 84 (кг) – фарби потрібно для ремонту 12 класів;
4 • 12 + 3 • 12 = 84 (кг)
3. Самостійна робота (завдання 191)
Учні виконують завдання в зошитах, один учень працює біля дошки. Перевіряють правильність виконання завдань.
9999; 1000;
69997; 6998; 69999; 7000; 70001.
VI. ДОМАШНЄ ЗАВДАННЯ
Завдання 192; 193 (с. 31).
VII. ПІДСУМОК УРОКУ
– Що нового дізналися на уроці?
– Чого вчилися?
– Хто був найактивнішим на уроці?