Десяткове наближення звичайного дробу
Розділ 2 Звичайні дроби
§13. Десяткове наближення звичайного дробу
При перетворенні звичайних дробів у десяткові можна отримувати нескінченні періодичні дроби. Виконуючи обчислення з такими дробами, зручно користуватися їх наближеннями, які отримують при округленні нескінченних дробів до певного розряду. Утворюється скінченний десятковий дріб, який називають десятковим наближенням звичайного дробу. Число, яке утворилося після округлення, тим точніше, чим більше десяткових знаків у його наближенні.
Приклад 1. 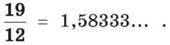
Десяткові наближення цього дробу такі:

– Щоб знайти десяткове наближення звичайного дробу, яке округлене до даного розряду, достатньо:
1) виконати ділення до наступного розряду;
2) знайдений результат округлити.
Приклад 2. Округлити до тисячних і обчислити: 4,5(3) + + 7,(18).
Розв’язання. Оскільки 4,5(3) = 4,5333… ” 4,533, а 7,(18) = 7,1818 ” 7,182, то 4,5(3) + 7,(18) ” 4,533 + 7,182 = =11,715.
Що розуміють під десятковим наближенням звичайного дробу? Як знайти десяткове наближення звичайного дробу, яке округлене до даного розряду?
289. Відомо, що 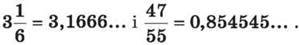 Знайди
Знайди
290. Відомо, що 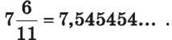 Знайди десяткове наближення цього звичайного дробу, округлене до:
Знайди десяткове наближення цього звичайного дробу, округлене до:
1) десятих; 2) сотих; 3) тисячних.
291. Знайди десяткове наближення дробу, округлене до сотих:
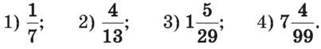
292. Знайди десяткове наближення дробу, округлене до десятих:
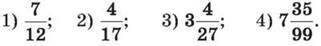
293. Велосипедист проїхав 43 км за 3 год. Знайди його швидкість. (Відповідь округли до тисячних км/год).
294. Поїзд проїхав 307 км за 6 год. Знайди його швидкість. (Відповідь округли до сотих км/год.)
295. Знайди корінь рівняння і округли його до сотих:
1) 13х = 7; 2) 8 : х = 125; 3) 56х = 103; 4) 17 : х = 6.
296. Знайди корінь рівняння і округли його до сотих:
1) 19х = 25; 2) 7 : х = 57.
297. Площа прямокутної ділянки землі 2730 м2, а довжина однієї зі сторін 55 м. Знайди довжину іншої сторони. (Відповідь округли до сотих метра.)
298. Обчисли висоту прямокутного паралелепіпеда, якщо його об’єм дорівнює 14 дм3, довжина – 3 дм, а ширина – 2,5 дм. (Відповідь округли до десятих дециметра.)
299. Велосипедист за першу годину проїхав 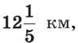 за другу –
за другу – 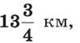 а за третю –
а за третю – 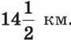 Знайди середню швидкість руху велосипедиста. (Відповідь округли до десятих км/год.)
Знайди середню швидкість руху велосипедиста. (Відповідь округли до десятих км/год.)
300. Округли періодичні дроби до сотих і обчисли: 1) 2,(76) + 4,(5) – 3,(1); 2) 4,0(3) – 2,(7) – 0,(24).
301. Скороти дріб:
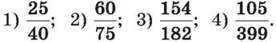
302. Обчисли:
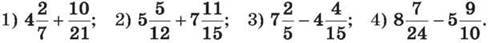
303. Чи можна число 64 подати у вигляді суми трьох простих чисел?
Завдання для перевірки знань № 2 (§ 8 – § 13)
1. Скороти дріб: 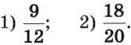
2. Запиши два дроби, які дорівнюють дробу 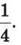
3. Порівняй дроби: 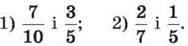
4. Виконай додавання: 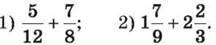
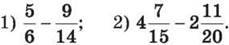
6. т Перетвори у десятковий дріб дане число (у випадку отримання нескінченного дробу ділення припини після визначення періоду):
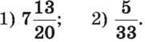
7. Знайди всі натуральні значення b, при яких є правильною нерівність:
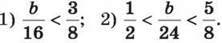
8. Розв’яжи рівняння, попередньо перетворивши десятковий дріб у звичайний, або мішані числа у десяткові дроби:
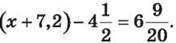
9. За першу годину розвантажили 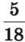 отриманого вантажу, за другу – 25 %, за третю –
отриманого вантажу, за другу – 25 %, за третю – 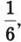 а за четверту – решту. Яку частину отриманого вантажу розвантажили за четверту годину?
а за четверту – решту. Яку частину отриманого вантажу розвантажили за четверту годину?
Додаткові вправи
10. Розв’яжи рівняння:
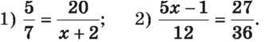
11. Знайди будь-які два дроби, кожний з яких більший за 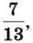 але менший від
але менший від 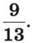
12. Як зміниться сума трьох доданків, якщо один з них збільшити на 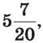 другий – збільшити на
другий – збільшити на 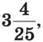 а третій – зменшити на 7,48?
а третій – зменшити на 7,48?