ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА
Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ
У розділі дізнаєтесь:
– що таке дільники і кратні натурального числа;
– які є ознаки подільності чисел;
– які числа називаються простими та як їх знаходити;
– як розкласти число на множники;
– що таке найбільший спільний дільник чисел та як його знаходити;
– що таке найменше спільне кратне чисел та як його знаходити;
– як застосувати вивчений матеріал на практиці

Решето ЕРАТОСФЕНА

§ 1. ДІЛЬНИКИ
Подивіться на малюнок 1. Ви бачите, що б яблук поділили на 2 купки по З яблука в кожній. Тут число б є діленим, число 2 – дільником, а число З – часткою. Але в яблук можна поділити і по-іншому – розкласти їх на 3 купки по 2 яблука в кожній. Тоді для діленого б число 3 є дільником, а число 2 – часткою. Це означає, що числа 2 і 3 є дільниками числа б. Водночас число б є кратним для кожного зі своїх дільників – і для числа 2, і для числа 3. Дільники і кратні є натуральними числами.

Мал. 1
Дільником числа називається таке число, на яке ділиться
Кратним числа називається таке число, яке ділиться надане число.
? Чи є інші дільники в числа б? Так. Число б ділиться ще на 1 і саме на себе. Отже, загалом у числа 6 є чотири дільники:
1; 2; 2; б.
Зверніть увагу:
Кожне натуральне число, починаючи з числа 2, має принаймні два дільники – число 1 і саме це число. Інші дільники шукають за спеціальними правилами.
Задача. Знайдіть усі дільники числа: 1) 7; 2) 12; 3) 25.
Розв’язання.
1) У числа 7 є принаймні два дільники – 1 і 7. На жодне інше натуральне число 7 не ділиться, тому в нього лише два дільники: 1 і 7.
2) Число 12 має принаймні два дільники – 1 і 12. Далі послідовно перевіряємо подільність числа 12 на натуральні числа від 2 до 11.12 : 2 = б, тому 2 і 6 – дільники числа 12. 12:3 = 4, тому 3 і 4 – теж дільники числа 12. На 5, 7, 8, 9, 10 і 11 число 12 не ділиться. Отже, дільниками числа 12 е числа: 1; 2; 3;4; 6; 12.
3) У числа 25 є принаймі два дільники: 1 25. На 2, 3 і 4, а також на числа від 6 до 24 це число не ділиться. 25 : 5 = 5, тому число 5 є дільником числа 25, при чому двічі. Але рівні дільники враховують лише один раз. Отже, у числа 25 не чотири, а три дільники: 1; 5; 25.
Запам’ятайте!
Натуральне число, яке має лише два дільники (1 і саме число), називається простим.
Натуральне число, яке має більше двох дільників, називається складеним.
Наприклад, 7 – просте число, а 12 і 25 – складені.
? Чи є 1 простим числом? А складеним? Ні, оскільки в числа 1 тільки один дільник. Отже, число 1 особливе. Вено і не просте, і не складене.
Зверніть увагу:
Найменшим простим числом є число 2.
Дізнайтеся більше
Щоб виписати деяку кількість простих чисел, можна скористатися способом, який придумав ще в III ст. до н. е. Ератосфен Кіренський (276 р. до н. е. – 194 р. до н. е.), грецький математик, астроном, географ і поет. На честь ученого цей спосіб носить назву “решето Ератосфена”. На малюнку (с. 4) ви бачите, як знаходили прості числа від 2 до 50. Спробуйте самостійно пояснити, як це робили.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Яке число називається дільником числа?
2. Яке число називається кратним числа?
3. На які два числа завжди ділиться будь-яке натуральне число більше за 1?
4. Яке натуральне число називається простим? Наведіть приклад.
5. Назвіть найменше просте число.
6. Яке натуральне число називається складеним? Наведіть приклад.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
1′. Чи кожне натуральне число має дільники?
2′. Чи правильно, що число 3 є дільником числа:
1)5; 2)9; 3)4; 4)12?
3′. Чи правильно, що число 12 є кратним числа:
1)5; 2)9; 3)4; 4)3?
4′. Назвіть: 1) три прості числа; 2) три складені числа.
5′. Чи є число 1:
1) простим числом; 2) складеним числом?
6°. Дано числа: 3; 4; 6; 8; 9. Випишіть ті з них, які є дільниками числа: 1)8; 2) 12; 3) 16; 4) 18.
7°. Дано числа: 2; 3; 5; 6; 8. Випишіть ті з них, які є дільниками числа: 1)9; 2) 15; 3) 32; 4) 40.
8°. Знайдіть усі дільники числа: 1) 8; 2) 14; 3) 28; 4) 39.
9°. Знайдіть усі дільники числа: 1) 9; 2) 11; 3) 25; 4) 36.
10°. Дано числа: 10; 12; 14; 16; 18; 20. Випишіть ті з них, які є кратними числа: 1) 4; 2) 6; 3) 3; 4) 8.
11°. Дано числа: 14; 18; 21; 24; 28; 30. Випишіть ті з них, які є кратними числа: 1) 6; 2) 7; 3) 10; 4) 3.
12°. Дід Мороз приніс дітям у дитячий садок подарунки і подарував кожній дитині однакову їх кількість. Скільки подарунків отримала кожна дитина, якщо в садочку 64 дитини, а подарунків було:
1)256; 2) 320; 3)448?
13°. На координатному промені позначте точку А(2) та ще чотири точки з координатами, кратними координаті точки А.
14°. На координатному промені позначте точку В(3) та ще три точки з координатами, кратними координаті точки В.
15°. Дано числа: 10; 11; 13; 15; 18; 23. Випишіть ті з них, які є:
1) простими; 2) складеними.
16°. Дано числа: 21; 25; 27; 29; 32; 37. Випишіть ті з них, які є:
1) простими; 2) складеними.
17°. Дано числа: 7; 8; 10; 13; 19; 24; 31; 34; 37; 39; 42; 43. Оберіть серед них ті, які мають:
1) тільки два дільники; 2) більше двох дільників.
18. Скільки дільників має число:
1) 125; 2) 216; 3) 256; 4) 400?
19. Знайдіть усі дільники числа:
1) 96; 2) 100; 3) 144; 4) 180.
20. Знайдіть усі дільники числа:
1) 84; 2) 72; 3) 125; 4) 120.
21. У магазині кольорові олівці продають у коробках по 16 олівців у кожній. Чи зможе вчитель малювання купити:
1) 48 олівців; 2) 64 олівці; 3) 96 олівців; 4) 120 олівців?
Якщо так, то скільки коробок?
22. У спортивних змаганнях беруть участь 108 школярів. Чи можна поділити їх на команди:
1) по 6 осіб; 2) по 12 осіб; 3) по 16 осіб; 4) по 24 особи?
Якщо так, то скільки буде таких команд?
23. Знайдіть усі двоцифрові числа, які є кратними числа:
1)8; 2)13; 3)16; 4)22.
24. Знайдіть усі двоцифрові числа, які є кратними числа:
1)9; 2)11; 3)12; 4)15.
25. Знайдіть усі трицифрові числа, менші від 400, для яких число 35 є дільником.
26. Знайдіть чотири найменші числа, дільниками яких є числа 6 і 8.
27. Чи можна записати просте число у вигляді:
1) суми двох парних чисел;
2) суми двох непарних чисел;
3) суми парного і непарного числа?
Відповідь поясніть. Наведіть приклади.
28*. Знайдіть будь-які чотири натуральні числа, які мають рівно три дільники. Яку закономірність ви помітили?
29*. Знайдіть будь-які чотири натуральні числа, які мають рівно чотири дільники. Яку закономірність ви помітили?
30*. Запишіть число 48 у вигляді різниці квадратів двох простих чисел, менших від 25.
31. Оксанка купувала в магазині цукерки й отримала 2 грн 25 к. здачі. Чи могла вона отримати здачу тільки монетами: 1) по 5 к.; 2) по 10 к.; 3) по 25 к.; 4) по 50 к.? Якщо так, то скільки було монет?
32. Вік Іринки, її старшої сестри Ольги, їхніх мами та бабусі – усе це є дільниками числа 165. Знайдіть вік сестри, мами та бабусі дівчинки, якщо відомо, що Іринці – 11 років.
ЗАДАЧІ НА ПОВТОРЕННЯ
33. Обчисліть:
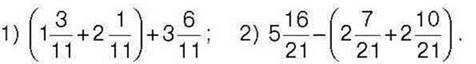
34. Магазин за перший день продав 180 кг помідорів, а за другий – 270 кг. На скільки відсотків більше магазин продав помідорів за другий день?


 (3 votes, average: 3.67 out of 5)
(3 votes, average: 3.67 out of 5)