Головна ⇒ 📌ГДЗ з математики ⇒ Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

Добуток різниці та суми двох виразів

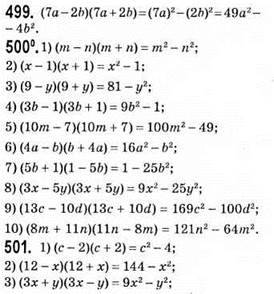
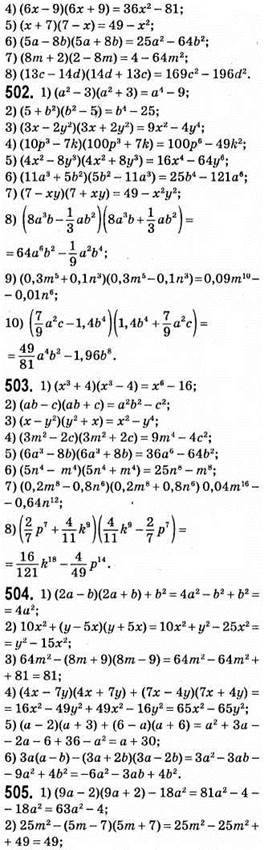
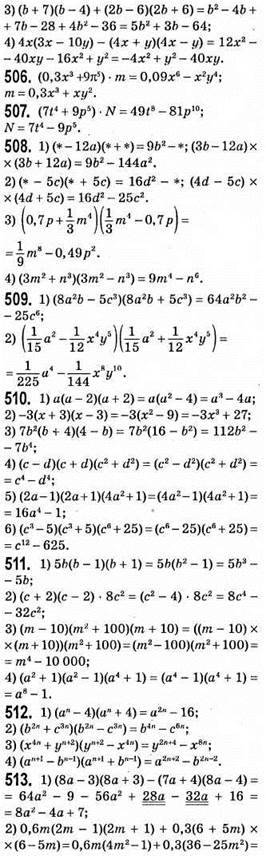
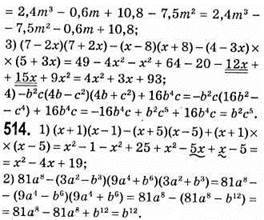
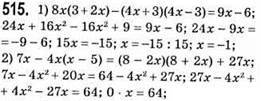
Рівняння коренів не має;

Добуток різниці та суми двох виразів

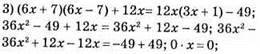
Коренем рівняння є будь-яке число;

Добуток різниці та суми двох виразів

Отже, значення виразу не залежить від значення змінної.

2) (2a – b)(2a + b) + (b – с)(b + с) + (с – 2а)(с + 2а) = 4а2 – b2 + b2 – с2 + с2 – 4а2 = 0. Отже, значення виразу не залежить від значень змінних.

518. (7n + 8)(7n – 8) – (5n + 10)(5n – 10) = 49n2 – 64 – 25n2 + 100 = 24n2 + 36 = 12(2n + 3) – ділиться наділо

на 12, бо 12 ділиться на 12.

Добуток різниці та суми двох виразів

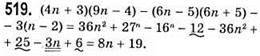
Значення виразу не ділиться наділо на 8, бо 8n ділиться на 8, а 19 не ділиться на 8.

Добуток різниці та суми двох виразів

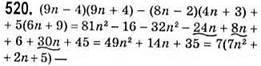
Ділиться націло на 7 при будь-якому значенні n, бо 7 ділиться на 7.

Добуток різниці та суми двох виразів

525. Нехай швидкість пішки x км/год, тоді швидкість руху на велосипеді (x + 8) км/год. Тоді відстань від села до станції дорівнює 3(x + 8) км, або 7x км. Отже,

7x = 3(х + 8); 7х = 3x + 24; 4x = 24; x = 24 : 4; x = 6 км/год – швидкість пішки.

6 + 8 = 14 км/год – швидкість руху на велосипеді.

14 • 3 = 42 км – відстань від села до станції.

526. Нехай з І мішка взяли л кг цукру, тоді з II

мішка взяли 4х кг цукру. В І мішку залишилося (60 – х) кг, а у II мішку залишилося (100 – 4х) кг. За умовою 60 – х = (100 – 4х) • 2; 60 – х = 200 – 8x; 8x – х = 200 – 60; 7x = 140; x = 140 : 7; х = 20 кг цукру взяли з І мішка; 4 • 20 = 80 кг цукру взяли з II мішка.

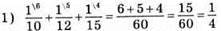527. Добуток різниці та суми двох виразів врожаю перевезуть автомобілі за 1 годину, працюючи разом;

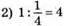Добуток різниці та суми двох виразів години необхідно автомобілям для перевезення всього врожаю.

528. 1) 7 • 7 • 7 • 7 • 7 = 75 = 16 807 жмень зерна рятують кішки;

2) 16 807 • 80 = 1 344 560 г = 1,344560 т = 1,34 т зерна щорічно рятують кішки.

Добуток різниці та суми двох виразів

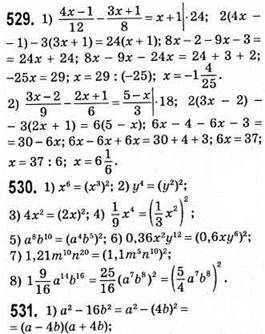
2) 25с2 + 9b2 – неможливо подати у вигляді різниці квадратів двох одночленів;

Добуток різниці та суми двох виразів

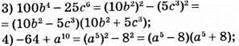
5) – a12 – 49c8 – неможливо подати у вигляді різниці квадратів двох одночленів;

Добуток різниці та суми двох виразів


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


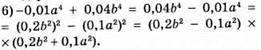
Related posts:

  1. Квадрат суми та квадрат різниці двох виразів 567. (5а + 3)2 = 25а2 + 30а + 9. 568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2. Рівняння коренів не має. 577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a […]...

  2. Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...

  3. Різниця квадратів. (Добуток різниці двох виразів на їх суму) Урок № 46 Тема. Різниця квадратів (Добуток різниці двох виразів на їх суму) Мета: відпрацювати навички застосування формули (a – b)(a + b) = a2 – b2 для перетворення цілих виразів у багаточлен стандартного вигляду із застосуванням переставного та сполучного законів множення та залежностей між знаком множників та добутком цих множників; поглибити знання та вміння […]...

  4. Різниця квадратів двох виразів 533. a2 – 144 = (a – 12)(a + 12). 534. -49 + b2 = b2 – 49 = b2 – 72 = (b – 7)(b + 7). 535. 1) а2 – 9 = а2 – 32 = (а – 3)(а + 3); 2) b2 + 1 – не можна розкласти на множники; 3) 4 […]...

  5. Сума й різниця кубів двох виразів 682. 1) Якщо b = -2, то (1 – b2)(1 + b2 + b4) = 1 – (b2)3 = 1 – b6 = 1 – (-2)6 = 1 – 64 = -63. 2) Якщо х = -1, то 2х3 + 7 – (х + 1)(х2 – х + 1) = 2х3 + 7 – (х3 […]...

  6. Розкладання на множники різниці квадратів двох виразів Розділ 1. ЦІЛІ ВИРАЗИ & 16. Розкладання на множники різниці квадратів двох виразів У тотожності (а – b)(а + b) = а2 – b2 поміняємо місцями ліву і праву частини. Матимемо: Цю тотожність називають формулою різниці квадратів двох виразів. Читають її так. Формулу різниці квадратів двох виразів застосовують для розкладання на множники двочлена а2 – […]...

  7. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і по­ловинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Фор­мування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...

  8. Множення різниці двох виразів на їх суму Розділ 1. ЦІЛІ ВИРАЗИ & 15. Множення різниці двох виразів на їх суму Помножимо різницю а – b на суму а + b: (а – b)(а + b) = а2 + ab – bа – b2 = а2 – b2. Отже, Одержали ще одну формулу скороченого множення. Її читають так. Розглянемо приклади застосування цієї формули. […]...

  9. ПОЛОВИНА, ТРЕТИНА І ЧВЕРТЬ. ПОРІВНЯННЯ ІМЕНОВАНИХ ЧИСЕЛ, ІМЕНОВАНОГО ЧИСЛА ТА СУМИ АБО РІЗНИЦІ ІМЕНОВАНИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗІВ. СКЛАДАННЯ ЗАДАЧ ЗА СХЕМАМИ ВИРАЗІВ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 83. ПОЛОВИНА, ТРЕТИНА І ЧВЕРТЬ. ПОРІВНЯННЯ ІМЕНОВАНИХ ЧИСЕЛ, ІМЕНОВАНОГО ЧИСЛА ТА СУМИ АБО РІЗНИЦІ ІМЕНОВАНИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗІВ. СКЛАДАННЯ ЗАДАЧ ЗА СХЕМАМИ ВИРАЗІВ Мета: ознайомити учнів з діленням на рівні частини; дати уявлення про половину, третину і чверть числа; вправляти у виконанні дій з іменованими числами; формувати вміння […]...

  10. ПИСЬМОВЕ МНОЖЕННЯ ТРИЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ. СКЛАДАННЯ ЗАДАЧ, ОБЕРНЕНИХ ДО ЗАДАЧ НА ЗНАХОДЖЕННЯ СУМИ ДВОХ ДОБУТКІВ; ЗАДАЧІ НА МНОЖЕННЯ ЧИСЛА НА ДОБУТОК. КРУГЛІ ЧИСЛА ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ФОРМУВАТИ ВМІННЯ ВИКОНУВАТИ ПИСЬМОВЕ МНОЖЕННЯ ТРИЦИФРОВОГО ЧИСЛА НА ОДНОЦИФРОВЕ; УДОСКОНАЛЮВАТИ ВМІННЯ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА МНОЖЕННЯ ЧИСЛА НА ДОБУТОК ТА ОБЕРНЕНІ ЗАДАЧІ НА СУМУ ДВОХ ДОБУТКІВ; ПОРІВНЮВАТИ СПОСОБИ СКЛАДАННЯ ПЛАНУ РОЗВ’ЯЗУВАННЯ ЗАДАЧІ ВІД ЧИСЛОВИХ ДАНИХ ТА ВІД ЗАПИТАННЯ; УТОЧНИТИ ЗМІСТ ТЕРМІНА “КРУГЛІ ЧИСЛА” I. Перевірка домашнього завдання Розв’язання задачі 41 один учень коментує […]...

  11. ПЕРЕВІРКА ДІЇ ДОДАВАННЯ. ВАРТІСТЬ МОНЕТ. ЗНАХОДЖЕННЯ СУМИ ВАРТОСТІ МОНЕТ. ПОРІВНЯННЯ ЗАДАЧ НА ЗНАХОДЖЕННЯ СУМИ І РІЗНИЦІ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 5. ПЕРЕВІРКА ДІЇ ДОДАВАННЯ. ВАРТІСТЬ МОНЕТ. ЗНАХОДЖЕННЯ СУМИ ВАРТОСТІ МОНЕТ. ПОРІВНЯННЯ ЗАДАЧ НА ЗНАХОДЖЕННЯ СУМИ І РІЗНИЦІ Мета: повторити правило перевірки додавання відніманням; формувати вміння складати приклади на віднімання з прикладів на додавання; розвивати уяву; виховувати інтерес до навчання. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. […]...

  12. ЗМІНА СУМИ Й РІЗНИЦІ ПРИ ЗМІНІ ЇХ КОМПОНЕНТІВ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ЗМІНА СУМИ Й РІЗНИЦІ ПРИ ЗМІНІ ЇХ КОМПОНЕНТІВ 67. “Розшифруй” записи. Якщо a + b = c, то (a + k) + b = c + k Якщо a – b = c, то (a + k) – b = c + k 68. Поясни за таблицею залежність зміни суми […]...

  13. Круглі числа. Периметр прямокутної ділянки. Знаходження суми і різниці багатоцифрових чисел (№№ 439-447) Тема. Круглі числа. Периметр прямокутної ділянки. Знаходження суми і різниці багатоцифрових чисел (№№ 439-447). Мета. Ознайомити учнів з круглими числами; узагальнювати прийоми розв’язування задач; закріплювати вміння знаходити периметр прямокутних ділянок за планом. Обладнання. Таблиця усних обчислень; таблиця “Периметр прямокутника”; “Картки для поточного контролю знань”. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашнього […]...

  14. Розкладання многочленів на множники за допомогою формул квадрата суми і квадрата різниці Розділ 1. ЦІЛІ ВИРАЗИ & 14. Розкладання многочленів на множники За допомогою формул квадрата суми і квадрата різниці Формули квадрата суми і квадрата різниці можна використовувати також для розкладання на множники виразів вигляду а2 + 2аb + b2 і а2 – 2ab +b2. Для цього перепишемо ці формули, помінявши місцями їх ліву і праву частини. […]...

  15. ПИСЬМОВЕ МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО. ЗАДАЧІ НА ЗНАХОДЖЕННЯ РІЗНИЦІ ДВОХ ЧАСТОК Мета: ознайомити учнів з письмовим множенням на двоцифрове число; вчити розв’язувати задачі, нерівності; розвивати мислення, математичну пильність; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Усні обчислення. Гра “Хто швидше?” – Знайдіть “ланцюжок” з відповіддю 240. – Довжина відрізка 15 см. Яка довжина 1/5 частини […]...

  16. Нумерація трицифрових чисел. Множення й ділення з числами 0 і 1. Задачі на знаходження суми двох добутків УРОК 2 Тема. Нумерація трицифрових чисел. Множення й ділення з числами 0 і 1. Задачі на знаходження суми двох добутків Мета: провести бесіду про значення числа 0 у записі числа; повторити множення й ділення з числами 1 і 0 та правила множення й ділення суми на число та ділення числа на добуток; розвивати в учнів […]...

  17. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ НА СУМІСНІ ДІЇ. ЗАДАЧІ НА ЗУСТРІЧНИЙ РУХ ДВОХ ТІЛ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: УЧИТИ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА ЗУСТРІЧНИЙ ОДНОЧАСНИЙ РУХ; ЗАКРІПЛЮВАТИ ВМІННЯ ЗНАХОДИТИ ЗНАЧЕННЯ ВИРАЗІВ НА СУМІСНІ ДІЇ І. Перевірка домашнього завдання 1. Серед записаних на дошці виразів знайти той, яким розв’язується задача 713. 294 • 2 : 7 • 6 294 : 7 : 2 • 6 294 : 2 : 7 • 6 […]...

  18. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ПЕРЕТВОРЕННЯ ВИРАЗІВ Цілі: – навчальна: удосконалити вміння застосовувати перетворення виразів до розв’язування задач; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати культуру усного та писемного мовлення; – виховна: виховувати старанність, дисциплінованість, працьовитість; Тип уроку : удосконалення і застосування знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...

  19. ПИСЬМОВІ ПРИЙОМИ МНОЖЕННЯ НА КРУГЛЕ ЧИСЛО РОЗВ’ЯЗУВАННЯ РІВНЯНЬ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ СУМИ ДВОХ ДОБУТКІВ Мета: вчити учнів застосовувати письмові прийоми множення на кругле число; вдосконалювати обчислювальні навички та вміння учнів розв’язувати задачі; розвивати мислення; виховувати уважність. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання – Прочитайте складені вирази. (630 + 210) : 3 = 280 (705 – 245) : 10 = 46 […]...

  20. Ділення суми на число. Ділення виду 39 : 3, 72 : 6 Ділення суми на число. Ділення виду 39 : 3, 72 : 6 882. Розв’язання: I спосіб: II спосіб: Відповідь: 8 платформ. 885. Розв’язання: Відповідь: на 10 кілограмів більша маса мішка цукру. 893. Розв’язання: Відповідь: 4 дні. 894. 8 + 4 + 2 = 14 (кг) (Спосіб ділення навпіл) 896. Розв’язання: 1) 42 : 7 = […]...

  21. Сумісні дії з багатоцифровими числами. Розширені задачі на знаходження суми двох добутків. Складання та розв’язування рівнянь. Ділення іменованих чисел (№№ 1076-1084) Тема. Сумісні дії з багатоцифровими числами. Розширені задачі на знаходження суми двох добутків. Складання та розв’язування рівнянь. Ділення іменованих чисел (№№ 1076-1084). Мета. Закріплювати вміння учнів знаходити значення виразів на сумісні дії з багатоцифровими числами; удосконалювати вміння розв’язувати задачі на знаходження суми двох добутків; вчити складати та розв’язувати рівняння, ділити іменовані числа. Обладнання. Таблиця для […]...

  22. Формули суми (різниці) однойменних тригономет­ричних функцій. Перетворення добутку тригономет­ричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригономет­ричних функцій. Перетворення добутку тригономет­ричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних три­гонометричних функцій і формул перетворення до­бутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спро­щення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...

  23. Нумерація шестицифрових чисел. Читання і записування, визначення числа тисяч у числі. Задачі, обернені до задач на знаходження суми двох добутків (№№ 267-274) Тема. Нумерація шестицифрових чисел. Читання і записування, визначення числа тисяч у числі. Задачі, обернені до задач на знаходження суми двох добутків (№№ 267-274). Мета. Закріплювати уміння учнів лічити сотнями тисяч, читати, записувати і розкладати числа на розрядні доданки; повторити прийоми порівняння багатоцифрових чисел; вправляти у розв’язуванні задач. Обладнання. Нумераційна таблиця; картки для опитування; таблиця усних […]...

  24. Складені задачі, що включають знаходження дробу від числа. Повторення правила множення числа на добуток Подання дробу як частки двох чисел (№№ 797-805) Тема. Складені задачі, що включають знаходження дробу від числа. Повторення правила множення числа на добуток Подання дробу як частки двох чисел (№№ 797-805). Мета. Закріплювати вміння учнів розв’язувати задачі, що включають знаходження дробу від числа; ознайомити учнів із дробами як частками двох чисел, вчити розв’язувати відповідні задачі; повторити правило множення числа на добуток та вправляти […]...

  25. ЗМІНА РІЗНИЦІ ЗАЛЕЖНО ВІД ЗМІНИ ОДНОГО З КОМПОНЕНТІВ ДІЇ ВІДНІМАННЯ. ПОРІВНЯННЯ ВИРАЗІВ БЕЗ ОБЧИСЛЕНЬ. МНОГОКУТНИКИ. ВИМІРЮВАННЯ ДОВЖИН СТОРІН МНОГОКУТНИКІВ. ПОБУДОВА МНОГОКУТНИКІВ ЗА ЗРАЗКОМ ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 62. ЗМІНА РІЗНИЦІ ЗАЛЕЖНО ВІД ЗМІНИ ОДНОГО З КОМПОНЕНТІВ ДІЇ ВІДНІМАННЯ. ПОРІВНЯННЯ ВИРАЗІВ БЕЗ ОБЧИСЛЕНЬ. МНОГОКУТНИКИ. ВИМІРЮВАННЯ ДОВЖИН СТОРІН МНОГОКУТНИКІВ. ПОБУДОВА МНОГОКУТНИКІВ ЗА ЗРАЗКОМ Мета: практично з’ясувати зміну різниці залежно від зміни одного з компонентів дії віднімання; вчити порівнювати вирази без обчислень, креслити фігури за зразком, […]...

  26. Читання і записування шестицифрових чисел в межах 200 тисяч. Лічба сотнями тисяч до 10 сотень тисяч. Мільйон. Задачі, обернені до здач на знаходження суми двох добутків (№№ 257-266) Тема. Читання і записування шестицифрових чисел в межах 200 тисяч. Лічба сотнями тисяч до 10 сотень тисяч. Мільйон. Задачі, обернені до здач на знаходження суми двох добутків (№№ 257-266). Мета. Навчити учнів лічити сотнями тисяч до 10 сотень тисяч; ознайомити із новою лічильною одиницею – мільйоном; повторити перетворення одиниць вимірювання довжини, усні прийоми обчислень множення […]...

  27. Розв’язування вправ на застосування перетворень виразів Урок № 56 Тема. Розв’язування вправ на застосування перетворень виразів Мета: узагальнити та систематизувати знання та вміння учнів щодо різних видів перетворень цілих виразів; відпрацювати навички застосування набутих знань та вмінь під час розв’язування завдань на доведення подільності. Тип уроку: узагальнення та систематизація знань. Хід уроку I. Організаційний момент Перевіряємо готовність учнів до уроку, повідомляємо […]...

  28. СКЛАДАННЯ ТА ОБЧИСЛЕННЯ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ, ЩО МІСТЯТЬ ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА ТА ЗАДАЧ, ОБЕРНЕНИХ ДО ЗНАХОДЖЕННЯ СУМИ ДОБУТКІВ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ФОРМУВАТИ НАВИЧКИ ШВИДКИХ ОБЧИСЛЕНЬ У МЕЖАХ ВИВЧЕНОГО МАТЕРІАЛУ, УДОСКОНАЛЮВАТИ ВМІННЯ СКЛАДАТИ ВИРАЗИ; РОЗВ’ЯЗУВАТИ ЗАДАЧІ, ЩО МІСТЯТЬ ЗНАХОДЖЕННЯ ЧАСТИНИ ЧИСЛА, ТА ЗАДАЧІ, ОБЕРНЕНІ ДО ЗНАХОДЖЕННЯ СУМИ ДОБУТКІВ; ВИБИРАТИ, ВИВЧАТИ ТА ОБГРУНТОВУВАТИ ДІЇ В РОЗВ’ЯЗАННІ ЗАДАЧ I. Перевірка домашнього завдання Розв’язання задачі 20 учень записує на дошці виразом 206 + (206 + 325) + […]...

  29. НУМЕРАЦІЯ ТРИЦИФРОВИХ ЧИСЕЛ: ЧИТАННЯ І ПОРІВНЯННЯ ЧИСЕЛ, ПОПЕРЕДНЄ І НАСТУПНЕ ЧИСЛА, ЗНАЧЕННЯ ЦИФРИ НУЛЬ У ЗАПИСІ ЧИСЛА. МНОЖЕННЯ І ДІЛЕННЯ З ЧИСЛАМИ 1 І 0. ЗАДАЧІ НА ЗНАХОДЖЕННЯ СУМИ ДВОХ ДОБУТКІВ Мета: вдосконалювати вміння учнів читати, записувати і порівнювати трицифрові числа, називати попереднє і наступне числа; повторити правила множення і ділення з числами 1 і 0; розвивати мислення; виховувати уважність. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання – Прочитайте складені рівняння. – Якою дією знаходили х у першому […]...

  30. Векторний добуток векторів 1. Векторний добуток векторів є вектором, а скалярний – числом. Векторний та скалярний добуток мають однакові властивості (крім комутативності). 2. За означенням модуля векторного добутку А отже, оскільки то 3. 1) За означенням У нашому випадку Скористаємось основною тригонометричною тотожністю: Тоді 2) За означенням У нашому випадку Скористаємось основою тригонометричною тотожністю: Тоді Оскільки 3) Рівність […]...

  31. Скалярний добуток векторів. Кут між векторами 233. А) Якщо то α = 90°, α – кут між векторами. Б) то α – гострий; А) то α – тупий. 234. А) Б) В) Г) 235. А) Б) 236. А) Б) В) Г) 237. А) Б) В) 238. α – кут між векторами А) Б) В) Г) 239. А) Звідси Б) Звідси В) […]...

  32. Задачі на знаходження трьох чисел за їх сумою і сумами двох доданків Задачі на знаходження трьох чисел за їх сумою і сумами двох доданків 1 Виконай обчислення письмово, перевір результати. 56 309 + 438 724 608 721 – 87 804 509 456 + 23 044 400 000 – 40 508 2 Згадай істотні ознаки задач на знаходження трьох чисел за трьома сумами. У чому полягає спосіб розв’язування […]...

  33. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  34. Обчислення різниці, коли зменшуване містить кілька нулів. Розширена задача на знаходження третього доданка УРОК 39 Тема. Обчислення різниці, коли зменшуване містить кілька нулів. Розширена задача на знаходження третього доданка Мета: звернути увагу учнів на труднощі під час виконання дії віднімання у випадку одночасного переходу через кілька розрядів; розвивати вміння розв’язати розширені задачі на знаходження третього доданка; вдосконалювати обчислювальні навички. Обладнання: картки для індивідуальної роботи, таблиці для усної лічби. […]...

  35. Знаходження значень виразів на сумісні дії першого ступеня та виразів з дужками. Задачі з буквеними даними (№№ 421-430) Тема. Знаходження значень виразів на сумісні дії першого ступеня та виразів з дужками. Задачі з буквеними даними (№№ 421-430). Мета. Закріплювати вміння учнів виконувати дії додавання і віднімання над багатоцифровими числами; навчати узагальнених прийомів розв’язування задач. Обладнання. Таблиця усних обчислень; картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка […]...

  36. Задачі на одночасний рух двох тіл у різних напрямках ст.48 Задачі на одночасний рух двох тіл у різних напрямках 1 Розв’яжи задачу. Із двох міст виїхали одночасно назустріч один одному два велосипедисти. Перший велосипедист рухався зі швидкістю 10 км/год, а другий – 11 км/год. Визнач відстань між містами, якщо велосипедисти зустрілися через 2 год. Іван склав обернену задачу – на знаходження швидкості руху другого велосипедиста. […]...

  37. Скалярний добуток векторів Геометрія Вектори Скалярний добуток векторів Скалярним добутком векторів і називається число . Позначення: . . Очевидно, що . Розподільна властивість скалярного добутку: . Кутом між ненульовими векторами і називається кут BAC. Кутом між будь-якими двома ненульовими векторами і називається кут між векторами, що дорівнюють даним і мають спільний початок. Вважають, що кут між однаково напрямленими […]...

  38. ПОРІВНЯННЯ ВИРАЗІВ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ДВІ ДІЇ РІЗНИХ СТУПЕНІВ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ І ДІЛЕННЯ Урок 56. ПОРІВНЯННЯ ВИРАЗІВ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ДВІ ДІЇ РІЗНИХ СТУПЕНІВ Мета: вдосконалювати обчислювальні навички, вміння розв’язувати прості і складені задачі на множення; закріплювати табличні випадки множення числа 2, вміння порівнювати числові вирази, знаходити значення виразів; розвивати логічне мислення; виховувати пізнавальний інтерес. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ […]...

  39. Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...

  40. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

Ви зараз читаєте: Добуток різниці та суми двох виразів
«
»