Головна ⇒ 📌Математика ⇒ Додавання двох чисел з різними знаками

Додавання двох чисел з різними знаками

Розділ 4 Раціональні числа і дії мідними

§39. Додавання двох чисел з різними знаками

Припустимо, що в понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув борг, тобто віддав Сергію 3 грн. Оскільки борг можна тлумачити як від’ємні числа, а майно – як додатні, то розрахунок між хлопцями можна подати так: -3 + 3 = 0.

Числа -3 і 3 – протилежні, їх сума дорівнює нулю. Сума двох протилежних чисел дорівнює нулю.

Приклад 1. 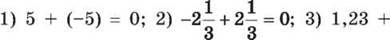(-1,23) = 0.

Якщо у понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув 2 грн, то

борг Івана Сергію становить 1 грн. Це можна записати так: -3 + 2 = -1.

У цій рівності модулі доданків дорівнюють 3 і 2, а модуль суми дорівнює 1, тобто модуль суми дорівнює різниці більшого і меншого модулів. Знак, який стоїть перед знайденим числом (мінус), збігається зі знаком доданка, модуль якого є більшим (числа -3).

Нехай у понеділок Іван заборгував Сергію 3 грн, а ввечері отримав від батьків 5 грн. Коли Іван віддасть борг, то в нього ще залишиться 2 грн. Тоді маємо: -3 + 5 = 2.

У цій рівності модулі доданків дорівнюють 3 і 5, а модуль суми 2, тобто модуль суми знову дорівнює різниці більшого і меншого модулів. Знак, який стоїть

перед знайденим числом (плюс), знову збігається зі знаком доданка, модуль якого є більшим (числа 5).

Маємо правило додавання двох чисел з різними знаками:

– щоб додати два числа з різними знаками, достатньо від більшого модуля доданків відняти менший модуль і записати перед знайденим числом знак того доданка, модуль якого більший.

Виконуючи обчислення, зручно спочатку визначити і записати знак суми, а потім у дужках записати різницю модулів.

Приклад 2. 1) -12 + 8 = – (12 – 8) = -4;

2) 10 + (-13) = – (13 – 10) = -3;

3) 13 + (-7) = +(13 – 7) = 6, або 13 + (-7) = 13 – 7 = 6;

4) -8 + 15 = +(15 – 8) = 7, або -8 + 15 = 15 – 8 = 7.

Розглянемо приклад додавання звичайних дробів з різними знаками, в якому спочатку треба порівняти модулі доданків і, лише після цього, застосувати правило.

Приклад 3.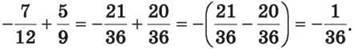

Якщо до числа а додати додатне число, то отримана сума буде більшою за а; якщо додати від’ємне число, то отримана сума буде меншою від а. Справді:

5 + 7 = 12 > 5; 5 + 3 = 8 > 5; 5 + 19 = 24 > 5;

5 + (-2) = 3 < 5; 5 + (-5) = 0 < 5; 5 + (-8) = -3 < 5.

Якому числу дорівнює сума протилежних чисел? Сформулюй правило додавання двох чисел з різними знаками. Наведи приклад, у якому сумою двох чисел з різними знаками є число додатне; нуль; число від’ємне.

1020. Назви знак суми:

1) -2 + 3; 2) 4 + (-5); 3) 8 + (-8); 4) -17 + 1.

1021. (Усно) Яка сума дорівнює нулю:

1) 2,1 + (-2); 2) 9 + (-9);

3) -8,5 + 1,2;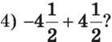

1022. (Усно) Обчисли:

1) -40 + 20; 2) 18 + (-7);

3) 500 + (-600); 4) -20 + 32.

1023. Знайди суму чисел:

1) 25 + (-15); 2) -110 + 37;

3) 4,9 + (-5); 4) -2,3 + 2,5.

1024. Знайди суму чисел:

1) 32 + (-12); 2) -115 + 15;

3) 4,2 + (-8,2); 4) -7,3 + 7,9.

1025. (Усно) Обчисли остаточний результат гри, якщо за дві партії нараховано:

1) -2 очки і +3 очки; 2) +5 очок і -7 очок;

3) -4 очки і +4 очки.

1026. Виконай додавання:

1) -4,254 + 6,44; 2) -6,7 + 5,9; 3) -4,8 + 4,8;

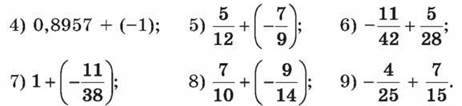
1027. Виконай додавання:

1) 5,75 + (-3,83); 2) -5,5 + 7,23; 3) -1 + 1,138;

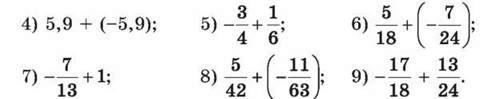
1028. Знайди значення виразу x + (-4,5), якщо x = 0,92; -0,8; 4,5; 5,2.

1029. Знайди значення виразу -5,2 + у, якщо у = 8,3; 5,2; -2,3; 0,8.

1030. (Усно) Які з нерівностей (рівностей) правильні, а які – ні:

1) 200 + (-40) > 0; 2) 7,39 + (-8,32) > 0;

3) 29,7 + (-29,7) < 0; 4) -14,7 + 14,7 = 0;

5) -82 + 81 < 0; 6) -20 + 2 < -20;

7) 28 + (-13) > 28; 8) -29 + (-29) < -29;

9) -8 + 0 =0?

1031. Обчисли:

1) (8,23 + (-5,47)) + (-3,84); 2) 4,47 + (-2,98 + 0,47).

1032. Обчисли:

1) (4,42 + (-10,8)) + 17,3; 2) -8,13 + (-3,42 + 4,59).

1033. Додай:

1) до суми чисел -56 і 37 число -19;

2) до числа 12 суму чисел -39 і 15.

1034. Додай до суми чисел -12 і 14 суму чисел 18 і -25.

1035. За даними таблиці знайди суму:

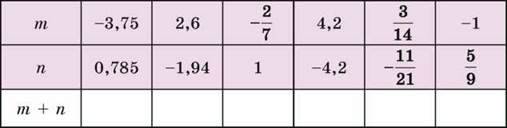
1036. За даними таблиці знайди суму:

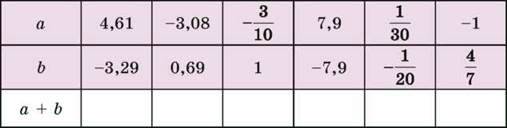
1037. Знайди значення виразу:

1) (-8,92 + 7,39) + (4,82 + (-3,17));

2) (4,39 + (-5,19)) + (-8,13 + 9,42).

1038. Знайди значення виразу:

1) (-5,17 + 4,92) + (7,42 + (-6,59));

2) (3,48 + (-2,17)) + (-7,18 + 4,49).

1039. Серед чисел -1,8; 1,7; 1,26; -2,5; 2,5; 1,59 знайди ті, які задовольняють нерівність x + (-4,2) > -2,6.

1040. Серед чисел -0,8; 4,7; 5; -0,41; 6,7; -0,9 знайди ті, які задовольняють нерівність -5,8 + у < -6,2.

1041. Постав замість * знак >, < або =, щоб утворилась правильна нерівність або рівність:

1) 200 + (-300) * 0; 2) 0 * -150 + 200;

3) 423 + (-423) * 0; 4) -8,2 + 13 * 5;

5) 19 + (-20,7) * -2; 6) -18 * -29 + 11.

1042. Постав замість * знак >, < або =, щоб утворилася правильна нерівність або рівність:

1) -180 + 270 * 0; 2) 0 * 130 + (-150);

3) 1,17 + (-1,17) * 0; 4) 4,8 + (-3,7) * 1;

5) -14,7 + 9,8 * -5; 6) -17,8 * -18 + 1,2.

1043. Знайди значення виразу:

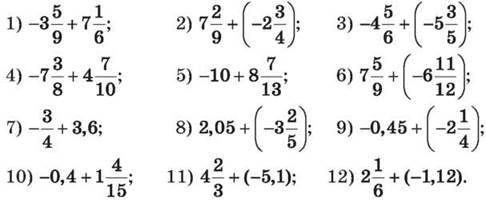
1044. Знайди значення виразу

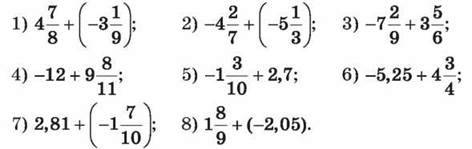
1045. Склади числовий вираз і обчисли його значення:

1) до числа додали суму чисел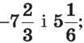

2) до суми чисел -12,42 і 13,67 додали число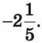

1046. Склади числовий вираз і обчисли його значення: до числа додали суму чисел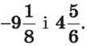

1047. Виконай дії: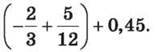

1048. Виконай дії: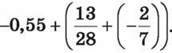

1049. Добери корінь рівняння і виконай перевірку:

1) у + (-3) = 5; 2) -8 + х = -3;

3) a + 8 = -3; 4) 7 + b = 2.

1050. Замість * постав знак + або -, щоб була правильною рівність:

1) (*20) + (*15) = -5; 2) (*15) + (*17) = -32;

3) (*7) + (*9) = 2; 4) (*11) + (*11) = 0;

5) (*29) + (*11) = 40; 6) (*19) + (*19) = -38.

1051. Замість * постав знак + або -, щоб була правильною рівність:

1) (*10) + (*15) = 5; 2) (*13) + (*12) = 25;

3) (*10) + (*10) = -20; 4) (*5) + (*7) = -2;

5) (*1) + (*1) = 0; 6) (*3) + (*2) = 1.

1052. До суми чисел 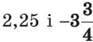додай число, взаємно обернене з числом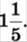

1053. Знайди суму, доданками якої є числа: обернене і протилежне до числа 7,5.

1054. Яка з нерівностей, де x < 0, є правильною, а яка – ні:

1) x + 3 > 3; 2) -5 + x < -5; 3) x + 7,6 < 7,6;

4) -5 + x > 0; 5) x + x > 0; 6) x + x < x?

1055. Яка з нерівностей, де у > 0, є правильною, а яка – ні:

1) -8 + y > -8; 2) y + (-2,8) < -2,8; 3) y + 7 < 0;

4) у + (-0,7) > -0,7; 5) y + у < 0; 6) y + у > у?

1056. Знайди значення виразу \а + b\ + а, якщо:

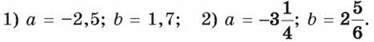
1057. Знайди у відсотках зміну величини:

1) від 5 т до 7 т; 2) від 10 см до 7 см;

3) від 40 г до 48 г; 4) від 1 ц до 90 кг;

5) від 80 коп. до 1 грн; 6) від 1 год до 45 хв.

1058. Швидкість велосипедиста 18 км/год. Вирази її у метрах за хвилину.

1059. Периметр прямокутника дорівнює 70 см. Знайди площу цього прямокутника, якщо його сторони відносяться як 3 : 4.

1060. Прямокутник з довжинами сторін 4 см і 9 см розріж на дві частини так, щоб з них можна було скласти квадрат.

(1 votes, average: 5.00 out of 5)

Ви зараз читаєте: Додавання двох чисел з різними знаками

« Хто такі птахи?

ВАЛОВА ПЕРВИННА ПРОДУКТИВНІСТЬ »

Related posts: