Дотична до кола, її властивості
Розділ 4. Коло і круг. Геометричні побудови
§ 22. Дотична до кола, її властивості
607.
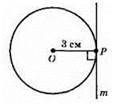
Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола.
608.
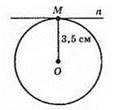
Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою 2 пряма n є дотичною до кола.
609. 1)
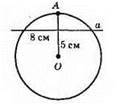
Пряма a перетинає коло.
2)
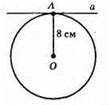
Пряма a дотикається
3)
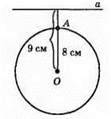
Пряма а не має з колом спільних точок.
610. 1) Пряма b не має з колом спільних точок.
2) Пряма b дотикається до кола.
3) Пряма b перетинає коло.
611. Оскільки KP – дотична до кола, то ОМ ⊥ KP, ∠OMP = 90°, ∠OMK = 90°.
1) Якщо ∠NMP = 35°, то ∠OMN = ∠OMP – ∠NMP = 90° – 35° = 55°.
2) Якщо ∠ONM = 50°, то ∠KMN = ∠OMK + ∠OMN = 90° + 50° = 140°.
612. Оскільки KP – дотична до кола, то ОМ ⊥ KP, ∠OMP = 90°, ∠OMK = 90°.
1) Якщо ∠OMN = 52°, то ∠NMP = ∠OMP – ∠OMN = 90° – 52° = 38°.
2) Якщо ∠KMN = 135°, то ∠OMN = ∠KMN – ∠OMK = 135° – 90° = 45°.
613.
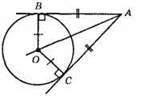
?OBA і? OCA – прямокутні, оскільки OB ⊥ AB, ОС ⊥ AC.
?OBA = ?ОСА за двома катетами (OB = ОС – як радіуси кола, AB = АС – як відрізки дотичних, проведених з однієї точки до кола).
З рівності трикутників маємо ∠BOA = ∠COA. Отже, ОА – бісектриса кута ВОС.
614.
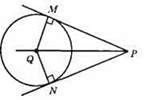
?QMP і? QNP – прямокутні, оскільки QM ⊥ MP, QN ⊥ NP.
?QMP = ?QNP за двома катетами (QM = QN – як радіуси кола, PM = PN – як відрізки дотичних, проведених з однієї точки до кола).
З рівності трикутників маємо ∠MPQ = ∠NPQ. Отже, PQ – бісектриса кута MPN.
615. Оскільки МК – дотична до кола, то ОМ ⊥ МК, ∠OMK = 90°. ?OMN – рівнобедрений, оскільки ОМ = ON – як радіуси кола. ∠OMN = ∠ONM = (180° – ∠MON) : 2 = (180° – 82°) : 2 = 49°. ∠NMK= 90° – ∠OMN = 90° – 49° = 41°.
Відповідь: 41°.
616. Оскільки МК – дотична до кола, то ОМ ⊥ МК, ∠OMK = 90°. ?OMN – рівнобедрений, оскільки ОМ = ON – як радіуси кола. ∠OMN = ∠ONM = ∠OMK – ∠NMK = 90° – 53° = 37°. ∠NOM = 180° -∠OMN – ∠ONM = 180° – 37° – 37° = 106°.
Відповідь: 106°.
617.
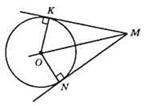
МК і MN – дотичні. OKA MK, ON A MN. З прямокутного? OKM: оскільки ОМ = 2OK, TO ∠KMO = 30°.
З прямокутного? ONM: оскільки ОМ = 2ON, то ∠OMN = 30°.
Отже, ∠KMN = ∠KMO + ∠OMN = 30° + 30° = 60°.
Відповідь: 60°.
618.
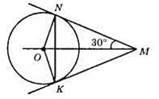
?ONM = ?OKM за двома катетами (ON = OK – як радіуси кола, MN = МК – як відрізки дотичних, проведених з однієї точки до кола). Отже, ∠NMO = ∠KMO = 30°.
?KMN – рівнобедрений, оскільки MN = МК, ∠MNK = ∠MKN = (180° – 60°) : 2 = 120° : 2 = 60°. Отже, ?KMN – рівносторонній і NK = NM = 7 см.
Відповідь: 7 см.
619. Нехай ∠A = 1/2∠DCB, тоді ∠B = 1/2∠DCB, оскільки зовнішній кут дорівнює сумі двох внутрішніх кутів, не суміжних з ним. Тоді, оскільки ∠B = ∠A, то трикутник ABC – рівнобедрений згідно з ознакою рівнобедреного трикутника.
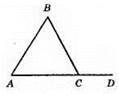
620. З прямокутного? ABC: AB = 2АС = 2 x 6 = 12 (см) (за властивістю прямокутного трикутника з кутом 30°). ∠ABC – зовнішній кут трикутника ADB. ∠BAD + ∠D = ∠ABC (за властивістю зовнішнього кута трикутника). ∠BAD = 30° – 15° = 15°. Отже, за ознакою рівнобедреного трикутника? ABD – рівнобедрений (∠BAD = ∠D). Отже, BD = АВ = 12 см.
Відповідь: 12 см.
621.