Головна ⇒ 📌Довідник з математики ⇒ Границя числової послідовності
Границя числової послідовності
Математика – Алгебра
Границя
Границя числової послідовності
Число a називається Границею послідовності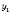 ,
,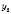 , …,
, …, 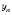 , …, якщо для будь-якого додатного числа
, …, якщо для будь-якого додатного числа  існує таке натуральне число
існує таке натуральне число 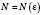 , що для всіх
, що для всіх 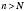 виконується нерівність
виконується нерівність
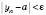 .
.
Позначеня: 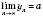 , або
, або 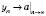 .
.
Послідовність 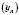
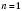 , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що для всіх
, 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що для всіх 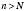 виконується нерівність
виконується нерівність 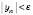 .
.Зверніть увагу: членами нескінченно малої послідовності можуть бути дуже великі числа.
Наприклад, послідовність
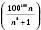 є нескінченно малою, але перші її члени є досить великими числами:
є нескінченно малою, але перші її члени є досить великими числами: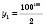 ;
; 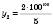 і т. д.
і т. д.Теорема. Якщо
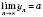 , то послідовність
, то послідовність 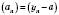
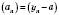 є нескінченно малою, то
є нескінченно малою, то 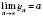 .
.Таким чином, дістанемо еквівалентне означення границі числової послідовності: число a називається границею числової послідовності
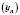 , якщо послідовність
, якщо послідовність 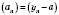 є нескінченно малою послідовністю.
є нескінченно малою послідовністю.Related posts:
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ Екологія – охорона природи ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ – фази розвитку прир. системи можуть проходити лише в еволюційно закріпленому порядку (історично, екологічно зумовленому), від відносно простого до складного, як правило, без випадання проміжних етапів (однак, можливо, з дуже швидким їх проходженням або еволюційно закріпленою відсутністю). Напр., метаморфоз комах з повним перетворенням може відбуватися лише […]...
- Практична робота 1. Координати комірок. Діапазон комірок. Введення й редагування числової, формульної та текстової інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 50 Практична робота 1. Координати комірок. Діапазон комірок. Введення й редагування числової, формульної та текстової інформації Мета: – формувати навички вводу числової, формульної та текстової інформації за допомогою програми опрацювання електронних таблиць; – повторити і закріпити засвоєні на попередньому уроці уміння та навичок щодо використання основних понять ЕТ; […]...
- Дільники і кратні Математика – Алгебра Подільність натуральних чисел Дільники і кратні Дільником натурального числа а називають натуральне число, на яке а ділиться без остачі. Кратним натуральному числу а називається натуральне число, яке ділиться на а без остачі. Приклади 1) Число 12 має 6 дільників: 1, 2, 3, 4, 6, 12. (Зверніть увагу: .) 2) Запишемо п’ять перших […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Розділ 2. ОЗДОБЛЕННЯ ВИРОБІВ АПЛІКАЦІЄЮ Урок № 7 Тема. ПОСЛІДОВНІСТЬ ВИГОТОВЛЕННЯ ВИРОБУ З АПЛІКАЦІЄЮ Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Мета уроку: Навчальна: забезпечити засвоєння учнями знань про технологічну послідовність виготовлення будь-якого виробу, формувати вміння планувати й виконувати технологічні операції; Розвивальна: розвивати логічне мислення, уміння аналізувати та співставляти; Виховна: виховувати потребу проявити […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Степінь Математика – Алгебра Подільність натуральних чисел Степінь Добуток n однакових множників, кожний із яких дорівнює а, називається n-м Степенем числа А і записується : , де n – натуральне число. Вираз називається степенем, число a – основою степеня, число n – показником степеня. Приклади ; ....
- Цикл з передумовою 2. Алгоритми з повторенням і розгалуженням 2.9. Цикл з передумовою У випадку, коли число повторень тіла циклу заздалегідь невідоме, а задається лише умова виконання циклу, використовуються цикли з умовою, а саме цикл з передумовою та цикл з післяумовою. У цьому параграфі розглянемо перший з них. Оператор циклу з передумовою має вигляд: While <умова> Do <тіло […]...
- Розв’язування задач і вправ. Самостійна робота № 1- МАТЕМАТИКА Мета: Навчити учнів розв’язувати задачі і вправи з теми “Натуральні числа ” Вчити учнів самостійно працювати. Учні повинні вміти: записувати натуральні числа словами і цифрами, порівнювати їх, розв’язувати задачі і вправи з натуральними числами. І. Перевірка домашнього завдання Клас поділено на дві команди Командам дається однакова кількість запитань. Хто більше набере балів. Та команда виграє. […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ РОЗДІЛ II ОДНОЧЛЕНИ &5. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Подивіться на малюнки 3 і 4. Ви бачите квадрат зі стороною а (мал. 3) і куб з ребром а (мал. 4). Ви знаєте, як знайти площу квадрата й об’єм куба та як записати результат за допомогою відповідних виразів: а2 і а3. Узагалі, добуток n рівних множників, кожний […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Зміни послідовності нуклеотидів ДНК МЕДИЧНА БІОЛОГІЯ Розділ 1 БІОЛОГІЧНІ ОСНОВИ ЖИТТЄДІЯЛЬНОСТІ ЛЮДИНИ 1.2. Молекулярно-генетичний і клітинний рівні організації життя 1.2.3. Спадковий апарат еукаріотичних клітин і його функціонування на молекулярному рівні 1.2.3.15. Зміни послідовності Нуклеотидів ДНК Мутації гена здебільшого є наслідком зміни послідовності нуклеотидів ДНК. Структурна класифікація мутацій гена: 1) заміна одних азотних основ іншими (транспозиція); 2) зміна кількості нуклеотидних […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- Прості та складені числа Розділ 1 Подільність натуральних чисел §4. Прості та складені числа Число 11 ділиться тільки на 1 і на себе. Іншими словами, число 11 має тільки два дільники: 1 і 11. У числа 8 чотири дільники: 1, 2, 4 і 8. Число 18 має шість дільників: 1, 2, 3, 6, 9 і 18. Такі числа, як […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...
- ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 24. ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА У п’ятому класі ви вивчали натуральні числа. Це числа, які використовують для лічби: 1; 2; 3; 4; … . Усі натуральні числа утворюють множину натуральних чисел. Цю множину позначають буквою N. Множина N має нескінченно багато елементів, оскільки натуральних чисел нескінченно […]...
- Логарифм числа. Основна логарифмічна тотожність Тема. Логарифм числа. Основна логарифмічна тотожність Мета уроку. Формування поняття логарифма числа. Познайомити учнів з основною логарифмічною тотожністю. І. Аналіз контрольної роботи II. Сприймання і усвідомлення поняття логарифма числа, основної логарифмічної тотожності Рівняння ах = b, де a > 0, а? 1, b > 0 (рис. 162) має єдиний корінь. Цей корінь називається логарифмом числа […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...