Композиції рухів і рівність фігур
446.
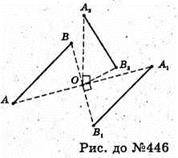
Образом відрізка АВ в результаті композиції центральної симетрії відносно т. О і повороту на кут 90° є відрізок А2В2.
447.
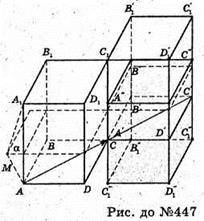
Образом даного паралелепіпеда в результаті композиції паралельного перенесення не вектор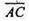 
та симетрії відносно площини а є паралелепіпед A′′B′′C′′D′′A′′1B’′1C′′1D”1.
448.
А) А1 симетрична А(1; -2; 5) відносно М.
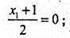
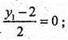
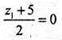
Паралельне перенесення на т.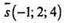 
переведе A1(-1; 2; -5) в т. A2(-2; 4; -1);
Б) A1 симетрична А відносно М.
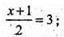
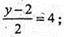
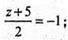x = 5y = 10z = -7. Отже, A1 (5; 10; -7).
Паралельне перенесення на т.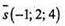 
переведе A1 (5; 10; -7) в т. A2(4; 12;-3).
449.
X2 + y2 + z2 – 2x + 4z = 9;
(х2 -2x + 1) + у2 + (z2 + 4z + 4) = 9 + 5;
(х – 1)2 + y2 +(z + 2)2 = 14,
O(1; 0; -2) – центр сфери.
При центральній симетрії відносно початку координат т. О перейде в
Т. О1(-1; 0; 2), при симетрії відносно площини (ху) O1, перейде в O2 О2(-1; 0; -2), при симетрії відносно площини (хоz) O2 перейде
Отже, в результаті даних композицій сфера перейде у сферу з центром
(-1; 0; -2) і тим самим радіусом. Така сфера задається рівнянням:
(x + 1) 2 + у2 + (z + 2)2 = 14 або
X2 + 2х + у2 + z2 + 4г = 9 або
X2 + у2 + z2 + 2х + 4z = 9 .
450.
Поворотом на кут, який дорівнює куту між відрізками, навколо прямої, що проходить через спільну точку відрізків і перпендикулярна до площини відрізків.
451.
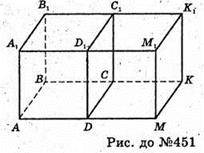
Ці куби можна сумістити паралельним перенесенням на AD.
452.
F1 і F мають спільну грань, тому ці куби можна відобразити один на одного за допомогою паралельного перенесення (див. № 451).
453.
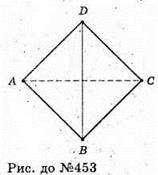
А) симетрія відносно точки – середина спільного перпендикуляра;
Б) поворотом;
В) поворотом.
454.
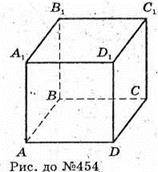
А) паралельним перенесенням на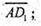
Б) паралельним перенесенням на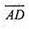 
і симетрією відносно прямої D1С;
В) паралельним перенесенням на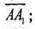
Г) симетрією відносно площини (ABC1D1);
Г) поворотом відносно точки їх перетину.
455.
Композиція двох поворотів може бути поворотом, може бути паралельним перенесенням або симетрією відносно площини.
456.
Може, якщо поворот виконано на 180°.
457.
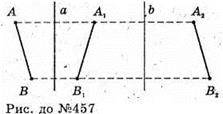
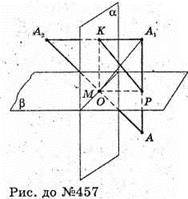
Відрізок A1В1 симетричний відрізку АВ відносно а, а відрізок А2В2 симетричний відрізку А1В1 відносно b; b? а. Неважко довести, що АА2В2В – паралелограм, звідси АВ? А2В2; АВ = А2В2. Відрізок А2В2 можна одержати з відрізка АВ шляхом паралельного перенесення на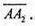 
458.
Т. A симетрична т. А1 відносно β, т. А1 симетрична т. А2 відносно α.
К – середина А1А2; Р – середина АА1; КР – середня лінія ΔA1АА2.
КА1РО – прямокутник. О1 – точка перетину діагоналей КР і OA1 .
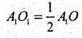(т. Фалеса). Тому О належить А1А2, але О належить прямій m –
Лінії перетину площин α і β. Отже АА2 перетинає m. До того ж А2О = OA
(т. Фалеса). Звідси А1 і А2 симетричні відносно прямої m.
459.
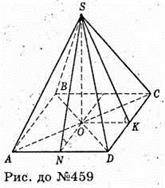
SABCD – правильна чотирикутна піраміда. При повороті навколо прямої SO ця піраміда суміститься сама з собою, при цьому ΔASC суміститься з ΔDSB; ΔSNO суміститься з ΔSKO, двогранний кут із ребром SD суміститься із двогранним кутом із ребром SC. Отже, ΔASC = ΔDSB, тобто діагональні перерізи рівні; ∠SNO = ∠SKO, тобто двогранні кути при основі рівні і двогранні кути при бічних ребрах рівні.
460.
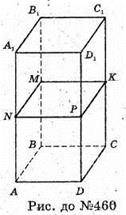
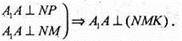
N – середина АА1 (за умовою).
Отже, А і А1 – симетричні відносно площини (ΝΜΚ).
Аналогічно: т. D і D1; С і С1; В і В1 – симетричні відносно площини (NMK).
Тоді паралелепіпед NMKPA1B1C1D1 і ABCDNMKP симетричні відносно площини (NMK), тому ці паралелепіпеди рівні.
Отже, площина (NMK) – площина симетрії паралелепіпеда.
461.
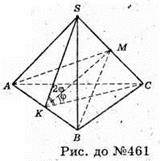
SABC – правильна трикутна піраміда. ∠SKC = 2φ. Переріз АМВ нахилений до основи під кутом φ, тобто ∠MKC = φ. Цей переріз розбив піраміду на дві частини піраміди SA3M і САВМ. Ці утворені фігури не завжди будуть рівні, а лише тоді, коли ΔSAB = ΔСАВ; тобто SB= ВС. Тобто, площина розтинає дану піраміду на дві рівні частини лише за умови, що ця піраміда – правильний тетраедр.
462.
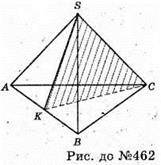
Площина (SKC) поділила піраміду SABC на два тетраедри: SAKC і SKPC. SK – апофема, ділить ΔSAB (рівнобедрений) на дві рівні частини SAK і SBK, до того ж AB + SK, тобто В і А симетричні відносно (SKC). Тетраедри SAKC і SBKC мають рівні основи і спільну висоту, вони рівні. Один із цих тетраедрів можна відобразити на інший за допомогою симетрії відносно площини (SKC).
463.
Так, ці тетраедри рівні.
464.
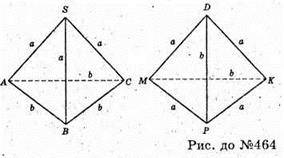
Ці тетраедри не обов’язково рівні. Якби було сказано, що а – бічні ребра, а b – ребра основи, то тетраедри рівні, а тетраедри SABC і DMPK не можуть бути рівні.
466.
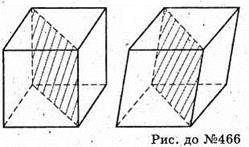
І в прямому, і в похилому паралелепіпеді діагональний переріз розбиває його на дві рівні призми.
467.
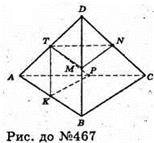
TN – середня лінія ΔАОС. TN? АС;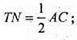 
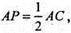
Звідси TN = АР. Аналогічно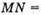 
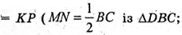
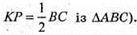ТМ = АK.
ΔTNM = ΔАРК, до того ж ΔTNM = ΔАРK лежать у паралельних площинах. Паралельне перенесення тетраедра АТРK на вектор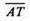 
дасть нам тетраедр TDNM. Отже, тетраедри АKРТ і TMND рівні.
468.
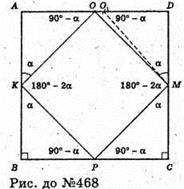
АВ, ВС, CD – три попарно перпендикулярні дзеркала.
З точки О виходить промінь на дзеркало AB. ∠AKO = ∠BKP = α, тоді, відбившись від дзеркала АВ в т. K промінь потрапляє на дзеркало ВС (в т. Р), відбиваючись в т. М на дзеркалі CD. Відбившись від т. М, промінь перетне промінь КО і т. O1. ∠BKP = α, тоді ∠BPK = 90° – α (з ΔKВР – прямокутний). ∠MPC = 90° – α, тоді ∠PMC = 90° – (90° – α) = α (з ΔРМС) і ∠DMO1= α, a ∠OMD = α, тому О і О1 збігаються (ОKРМ – паралелограм). Отже, промінь повернувся до свого джерела т. О.
(1 votes, average: 5.00 out of 5)
Loading...