Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Конус. Площа поверхні та об’єм конуса

Конус. Площа поверхні та об’єм конуса

УРОК № 57

Тема. Конус. Площа поверхні та об’єм конуса

Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів.

Тип уроку: комбінований.

Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів.

Вимоги до рівня підготовки учнів: пояснюють, що таке конус та його елементи; зображують і знаходять на рисунку конус; записують і пояснюють формули площі поверхні та об’єму

конуса; застосовують вивчений матеріал до розв’язування задач, утому числі прикладного змісту.

Хід уроку

І. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли в учнів при розв’язуванні задачі.

Розв’язання

V = ?R2H, R = 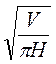= = 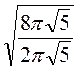= 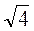2 (см).

Отже, AD = 2R = 2 • 2 = 4 (см). CD = 2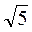 cм (рис. 269).

Із трикутника ACD маємо:

АС = 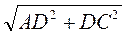= = 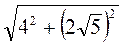= 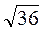6 (см).

Sбічн = 2nRH = 2n • 2 • 2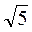

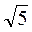class=""/> = 8

N (см2).

Відповідь. 6 см і 8 n см2.

Фронтальна бесіда

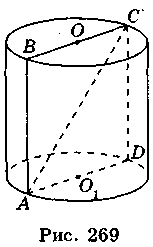
Циліндр утворено в результаті обертання прямокутника навколо сторони, яка утворює з діагоналлю прямокутника кут?, довжина діагоналей дорівнює d (рис. 270). Визначте, які з наведених тверджень є правильними, а які – неправильними.

А) Висота циліндра дорівнює dcos?.

Б) Радіус циліндра дорівнює dsin?.

В) Площа повної поверхні циліндра дорівнює 2nd2 cos?(cos? + sin?).

Г) Об’єм циліндра дорівнює nd3 sin2? cos?.

II. Поетапне сприймання й усвідомлення нового матеріалу

Конус та його елементи

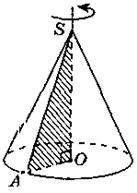
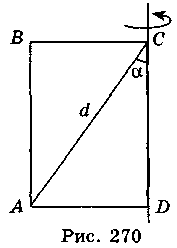
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів (рис. 271).

Якщо прямокутний трикутник SAO обертається навколо катета SO, то його гіпотенуза описує бічну поверхню, а катет О А – круг – основу конуса. Радіус цього круга називається радіусом конуса; точка S, відрізок SA, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

Осьовий переріз конуса – переріз конуса площиною, яка проходить через його вісь. Усі осьові перерізи конуса – рівні між собою рівнобедрені трикутники. На рис. 272 ?SAB – осьовий переріз конуса (SA = SB). Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи.

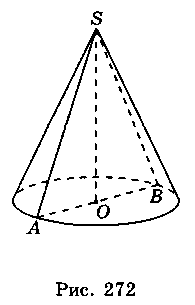
У прямого кругового конуса основа висоти збігається з центром основи. На рис. 272 SO – висота конуса.

Завданий класу

1. Наведіть приклади побутових предметів, які мають форму конуса. 2. Радіус основи конуса дорівнює 6 см, висота – 8 см. Знайдіть твірну конуса. 3. Твірна конуса дорівнює 5 см, а діаметр основи – 6 см. Знайдіть площу осьового перерізу конуса.

Площа поверхні та об’єм конуса

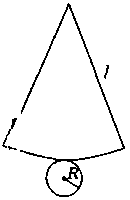
Бічну поверхню конуса, як і бічну поверхню циліндра, можна розгорнути на площину, розрізавши її по твірній (рис. 273).

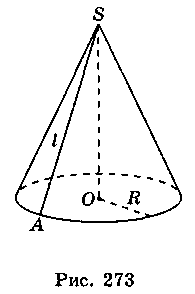
Розгорткою бічної поверхні конуса є круговий сектор, радіус якого дорівнює твірній конуса, а довжина дуги сектора – довжині кола основи конуса (рис. 274).

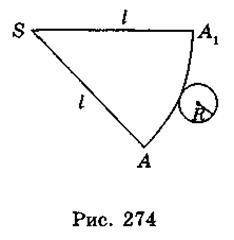
Площею бічної поверхні конуса будемо вважати площу її розгортки. Виразимо площу бічної поверхні конуса Sбічн через його твірну l і радіус основи R. Площа кругового сектора – розгортки бічної поверхні конуса (рис. 418) – дорівнює 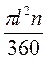, де n – градусна міра дуги АА1, тому Sбічн = 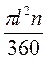. (1).

Виразимо п через l і R. Оскільки довжина дуги АА1 дорівнює 2nR (довжині кола основи конуса), то 2nR = 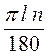, звідси n = .

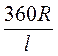Підставивши цей вираз у формулу (1), одержуємо: Sбічн = 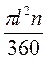= 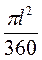• 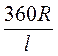= nRl.

Таким чином, площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну: Sбічн = nRl.

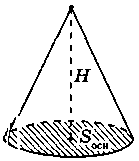
Площею повної поверхні конуса називається сума площ бічної поверхні та основи. Для обчислення площі повної поверхні конуса Sкон одержуємо:

Sкон = Sбічн + Sосн, Sкон = nRl + nR2 = nR(l + R).

Об’єм конуса дорівнює третині добутку площі його основи на висоту: V = NR2H.

Poзв’язування задач

1. Висота конуса дорівнює 6 см, радіус основи – 8 см. Знайдіть бічну поверхню конуса. 2. Твірна конуса дорівнює 5 см, висота – 4 см. Знайдіть площу повної поверхні конуса. 3. Осьовий переріз конуса – правильний трикутник, сторона якого дорівнює 6 см. Знайдіть бічну поверхню конуса. 4. Висота конуса дорівнює 6 см, твірна – 10 см. Знайдіть об’єм конуса. 5. Осьовий переріз конуса – прямокутний трикутник із гіпотенузою 12 см. Знайдіть об’єм конуса.

Учні складають конспект (зразок наведено у табл. 13).

Таблиця 13

Конус
	Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів. SO – вісь, SO – висота, SA – твірна, АО – радіус
Площа поверхні конуса
	Sкон = Sбічн + Sосн, Sбічн = nRl, Sосн = nR2
Об’єм конуса
	V = NR2H

III. Закріплення й осмислення нового матеріалу
Розв’язування задач

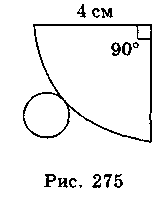
1. На рис. 275 зображено розгортку конуса, Знайдіть площу бічної поверхні та об’єм конуса. (Відповідь. 4n см2, 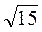N см3)

2. Купа щебеню має форму конуса, твірна якого дорівнює 6 м, а кут між твірною і висотою цього конуси становить 60°. Знайдіть об’єм щебеню. (Відповідь. 27м3) 3. Твірна конуса дорівнює l і утворює з висотою конуса кут?. Знайдіть площу бічної поверхні та об’єм конуса. (Відповідь. nl2 sin?; Nl3 sin2? cos?)

IV. Домашнє завдання

1. Вивчити формули площі поверхні та об’єму конуса. 2. Розв’язати задачу.

Твірна і висота конуса дорівнюють 15 см і 9 см. Знайдіть площу його поверхні та об’єм.

V. Підбиття підсумків уроку

Запитання до класу

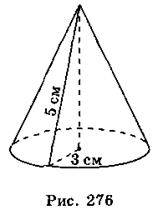
1. Дайте означення прямого кругового конуса. 2. Що таке осьовий переріз конуса? 3. Чому дорівнює площа бічної поверхні конуса? 4. Чому дорівнює площа поверхні конуса? 5. Чому дорівнює об’єм конуса? 6. Радіус основи конуса дорівнює 3 см, а твірна – 5 см (рис. 276). Визначте, які з наведених тверджень є правильними, а які – неправильними.

А) Довжина кола основи конуса дорівнює 9n см.

Б) Площа основи конуса дорівнює 9n см2.

В) Площа бічної поверхні конуса дорівнює 15n см2.

Г) Висота конуса дорівнює 4 см.