Кут. Позначення кутів
УРОК 32
Тема. Кут. Позначення кутів
Мета: закріпити знання учнями понять “кут”, “елементи кута”, “рівні кути”, “бісектриса кута”; відпрацювання навичок будувати, розрізняти кути, знаходити на рисунках рівні кути (розвиток окоміру).
Тип уроку: засвоєння навичок та вмінь.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
(Робота з сигнальними картками)
Ігровий момент
Учитель. Любі друзі! Чи знаєте ви, що у вашому класі з’явився новий учень – Петрик Тяпляпкін? Але сьогодні
Після цього учні виконують усні вправи.
1. Назвіть кути, зображені на рис. 30.
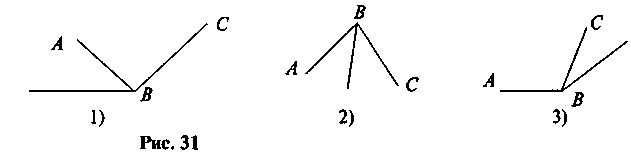
2. Чи проходить промінь між сторонами кута ABC! Чи є він бісектрисою кута? (рис. 31)
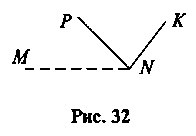
3. Учитель. Зараз я накреслю кут MNK, NP – його бісектриса (рис. 32). Тепер я витру промінь NM. Як його поновити?
ІІІ. Відпрацювання навичок
1) №№ 303; 305 – за підручником.
2) Практична робота з прозорим папером.
Методика проведення практичної роботи
Учням роздаються аркуші із завданням і рисунками, і аркуші прозорого паперу, на який вони можуть переносити зображення кутів. На початку роботи вчитель пояснює, як це робиться. Відповіді заносяться до листа відповідей і здаються, завдання перевіряються у класі, і проводиться корекція знань за необхідності.
Завдання 1. Який з поданих кутів дорівнює куту ABC (рис. 33)?
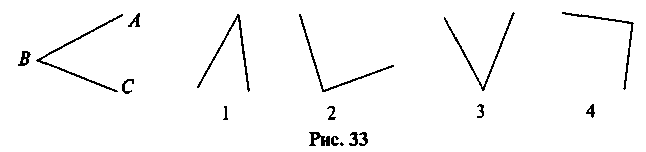
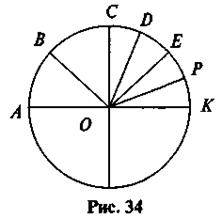
Завдання 2. Для якого з перелічених кутів промінь ОЕ є бісектрисою (рис. 34)?
1) 
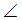DOK; 2) 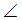COK; 3) 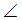AOC; 4) COP.
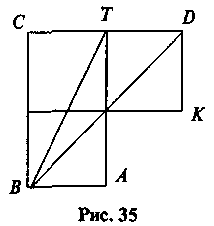
Завдання 3. У якому з поданих на рис. 35 4-х випадків правильно названо бісектрису кута?
1) ВТ – бісектриса кута ABC;
2) DB – бісектриса KDC;
3) ВТ – бісектриса DBC;
4) ТВ – бісектриса ATC.
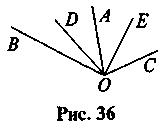
Завдання 4. Бісектрисою якого з наведених кутів є промінь ОЕ (рис. 36)?
1) BOD; 2) AOC; 3) 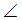COD; 4) 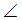DOB.
III. Підсумок уроку
Ігровий момент
Учитель. Два учні 5-го класу – Стьопа Смєкалкін і Петрик Тяпляпкін за допомогою одного й того ж косинця накреслили на дошці 2 кути:
Стьопа | Петрик |
|
|
Петрик сказав: мій кут більший, бо в нього сторона довша. Чи правильно міркує Петрик?
VI. Домашнє завдання
П. 11, № 296 (усно); № 304; 286 (11; 12); 279.