КУТИ ТА ЇХ ВИМІРЮВАННЯ
РОЗДІЛ 1
ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА
§ 5. КУТИ ТА ЇХ ВИМІРЮВАННЯ
Подивіться на малюнок 65. Ви бачите дві прямолінійні стежки, що виходять від одного пенька. Стежки нагадують промені, а пеньок – точку, що є спільним початком цих променів. Цей приклад дає уявлення про геометричну фігуру кут (мал. 66).

Мал. 65

Мал. 66
Кутом називається геометрична фігура, утворена двома променями зі спільним початком.
Промені називаються сторонами кута, а їх спільний початок – вершиною
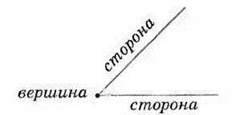
Мал. 67
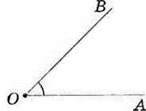
Мал.68
На малюнку 68 ви бачите кут із вершиною О і сторонами ОА і ОВ.
Коротко записують: ∠ АОВ (А ВОА). Знак ∠. заміняє слово “кут”. Даний кут можна позначити лише назвою його вершини, наприклад, ∠ О.
Зверніть увагу:
Якщо кут позначено трьома буквами, то середня буква в його назві відповідає вершині кута.
Подивіться на малюнок 69. На прямій DC позначено точку О. Утворилось два промені – ОС і OD. Ці промені виходять зі спільного початку О, тому теж утворюють кут – ∠ DOC. Такий кут називається розгорнутим.
Мал. 69
Ви знаєте, що відрізок характеризує його довжина. Так само кут характеризує його міра. Щоб виміряти кут, треба обрати одиницю вимірювання – одиничний кут. Найчастіше роблять це так.
Розгорнутий кут поділяють на 180 рівних частин (мал. 70) і одну з них обирають за одиничний кут. Його міру називають градусом.
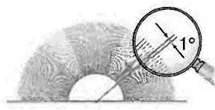
Мал. 70
Іменоване число “1 градус” коротко записують так: 1°. Для кожного кута можна визначити його градусну міру.
? Яка градусна міра розгорнутого кута? 180°, оскільки 180 ∙1° = 180°.
Кути вимірюють транспортиром (мал. 71, 72). Ви бачите, що на транспортирі нанесено дві шкали – внутрішню і зовнішню. На одній шкалі числа зростають проти годинникової стрілки, а на іншій – за годинниковою стрілкою. На малюнках 71 і 72 показано, як вимірювати кут АОВ залежно від розміщення його сторін. Ви бачите, що в обох випадках градусна міра кута АОВ дорівнює 120°.
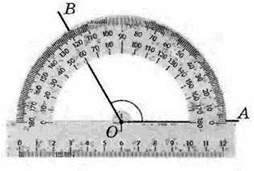
Мал. 71
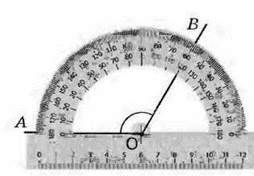
Мал. 72
Коротко говорять: “Кут АОВ дорівнює 120°” і запитують: ∠AOB -120°.
Задача 1. За допомогою транспортира і лінійки побудуйте кут BCD, що дорівнює 65°.
Розв’язання. Позначимо точку С – вершину кута (мал. 73). Проведемо промінь СВ (мал. 74). За допомогою транспортира визначимо розміщення точки D, через яку проходитиме сторона CD шуканого кута з градусною мірою 65° (мал. 75). Проведемо промінь CD (мал. 76).
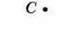
Мал. 73

Мал. 74
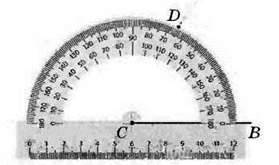
Мал. 75
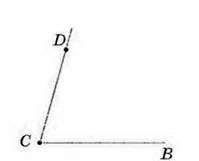
Мал.76
Для порівняння кутів користуються їх градусними мірами. На малюнку 77 ви бачите, що ∠ АОВ = 60° і ∠ LMN = 60°, тому кути АОВ і LMN – рівні. Кут CDE дорівнює 80°, тому він більший за ∠ АОВ. Відповідно, ∠АОВ менший від ∠ CDE.
Коротко записують: ∠ АОВ = ∠ LMN, ∠ CDE > ∠ АОВ, ∠ АОВ < ∠ CDE. На малюнку рівні кути позначають однаковою кількістю дужок (див. мал. 77).
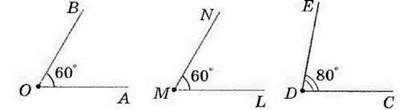
Мал. 77
На практиці для порівняння кутів, як і відрізків, можна скористатися способом: накладання.
1. Рівні кути мають рівні градусні міри.
2. Із двох кутів більшим є той кут, градусна міра якого більша.
Кути, менші від розгорнутого, можна поділити натри види – прямі, гострі чи тупі кути. Кут, що дорівнює 90°, називають прямим (мал. 78). Кут, менший від 90°, називають гострим (мал. 79), а більший за 90° – тупим (мал. 80).
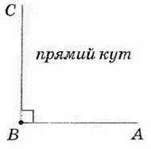
Мал. 78
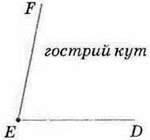
Мал. 79
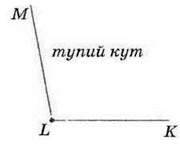
Мал. 80
На малюнку прямий кут позначають знаком “┘”.
Прямий кут можна будувати за допомогою косинця (мал. 81).
На окремому аркуші зобразимо будь-який кут, а потім зігнемо аркуш так, щоб сторони кута сумістилися. Лінія згину намітить такий внутрішній промінь кута, який ділить даний кут навпіл. Його називають бісектрисою кута. На малюнку 82 ви бачите кут АОВ і його бісектрису – промінь ОС. Для кутів АОС і СОВ, які бісектриса ОС утворює зі сторонами кута АОВ, виконується рівність:
∠ АОС = ∠ СОВ.
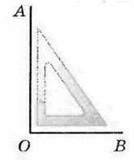
Мал. 81
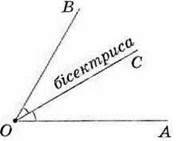
Мал. 82
Мал. 83
Мал. 84
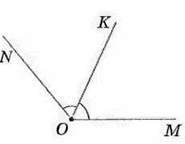
Задача 2. ∠ MON = 130°. Промінь OK – його бісектриса (мал. 83). Яка градусна міра кута МОК?
Розв’язання. Оскільки ОК – бісектриса кутаMON, то ∠ МОК = ∠ KON = ∠ MON : 2 = 130°: 2 = 65°.
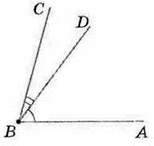
Із вершини В кута ABC проведемо будь-який внутрішній промінь BD (мал. 84). Він розбиває кут ABC на два кути ABD і DBC. Ці кути менші від кута ABC, але їх сума дорівнює куту ABC. Отже, ∠ ABC =∠ABD + ∠DBC. Кути ABD і DBC – це частини кута ABC.
Задача 3. Промінь OP – внутрішній промінь кута MON (мал. 85).
Яка градусна міра кута PON, якщо ∠ MON = 145° і ∠МОР = 60°?
Розв’язання,
Оскільки ∠ MON = ∠ МОР + ∠ PON, то ∠ PON = ∠MON – ∠ МОР. Звідси ∠ PON = 145° – 60° = 85°.
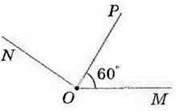
Мал. 85
1) градусна міра кута дорівнює сумі градусних мір його частин;
2) бісектриса кута ділить його навпіл.
Дізнайтеся більше
1. Знак кута “∠” увів французький математик П. Ерігон у XVII ст.
2. Назва “градус” походить від латинського слова gradus, що означає “крок” або “сходинка”. Поняття градуса вперше застосовував давньогрецький вчений Гітолемей (близько 178-100 р. до н. е.), який для цього ділив коло на 360 частин. Сучасне позначення градуса “°” увів французький медик і математик Жак Пелетьє дю Ман у 1558 році.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
140. Назвіть кожен із кутів, зображених на малюнку 86. Який із цих кутів: 1) розгорнутий; 2) прямий; 3) гострий; 4) тупий?

Мал. 86
141. Назвіть рівні кути, зображені на малюнку 87.
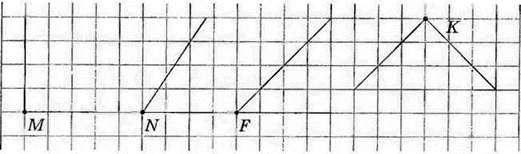
Мал. 87
142.Оленка дала означення куту: “Фігуру, утворену двома променями, називають кутом”. Чи отримає вона гарну оцінку?
143. Скільки кутів зображено на малюнку 88? Визначте градусну міру цих кутів. Зробіть відповідні записи.
144. Скільки кутів зображено на малюнку 89? Визначте градусну міру цих кутів. Зробіть відповідні записи.
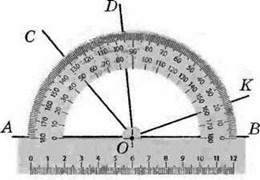
Мал. 88
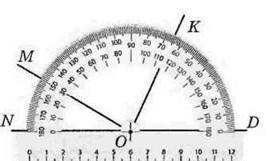
Мал. 89
145. Визначте градусну міру кутів, зображених на малюнку 90, якщо ∠ АОВ = ∠ ВОС = ∠ COD = ∠ DO А:
1) ∠AOB; 2) ∠AOK; 3) ∠NOD; 4) ∠ KON.
146. Визначте градусну міру кутів, зображених на малюнку 91, якщо ∠ COD = ∠ DOM = ∠ MON = ∠ NOC:
1) ∠KOD; 2) ∠KOM; 3) ∠MOP; 4) ∠ COP.
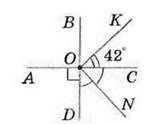
Мал. 90
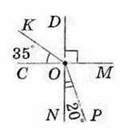
Мал. 91

Мал. 92
147. Зобразіть кут, градусна міра якого дорівнює:
1)25°; 2)120°; 3)40°; 4)90°.
148. Зобразіть кут, градусна міра якого дорівнює:
1)30°; 2)150°; 3)65°; 4)170°.
149. На який кут повернеться хвилинна стрілка годинника на малюнку 92 за:
1)5хв; 2)15хв; 3)20хв; 4)30хв?
150. Який кут утворюють годинна і хвилинна стрілки годинника о:
1) 2 год 00 хв; 2) 3 год 00 хв; 3) 5 год 00 хв; 4) 6 год 00 хв?
151. Проведіть бісектрису кута, градусна міра якого дорівнює:
1)70°; 2)160°; 3)90°.
152. Проведіть бісектрису кута, градусна міра якого дорівнює:
1)50°; 2)120°; 3)150°.
153. Проведіть промінь ОМ. За допомогою транспортира по один бік від променя ОМ побудуйте кут MON, градусна міра якого дорівнює 45°, а по інший бік – кут МОК, градусна міра якого – 65. Чому дорівнює градусна міра кута NOK?
154. Накресліть два кути зі спільною стороною:
1) що утворюють розгорнутий кут;
2) що не утворюють розгорнутий кут.
Чи можуть ці кути мати однакову градусну міру? Відповідь поясніть.
155. Як, згинаючи аркуш паперу, можна дістати кут, що дорівнює 45°? Відповідь поясніть.
156. Промінь BD – бісектриса ∠ABC. Знайдіть градусну міру: 1) ∠ DBC, якщо ∠ ABC = 150°; 2) ∠ ABC, якщо ∠ ABD = 28°.
157. Промінь ОК – бісектриса ∠AOB. Знайдіть градусну міру:
1) ∠ АОК, якщо ∠ АОВ – 70°; 2) ∠ АОВ, якщо ∠ КОВ = 55°.
158. Промінь ОВ – внутрішній промінь кута АОС. Знайдіть градусну міру:
1) ∠ АОС, якщо ∠ АОВ = 38° і ∠ ВОС = 44°;
2) ∠АОВ, якщо ∠АОС= 124° і ∠ ВОС = 33°;
3) ∠ ВОС, якщо ∠ АОС = 62° і ∠ АОВ = 20°.
159. Промінь ON – внутрішній промінь кута МОК. Знайдіть градусну міру:
1) ∠ МОК, якщо ∠ MON = 71 ° і ∠ NOK = 56°;
2) ∠ NOK, якщо ∠ МОК = 94° і ∠ MON = 57°.
160. Прямий кут поділили внутрішніми променями на рівні кути. Знайдіть градусну міру цих кутів, якщо отримано:
1) 2 кути; 2) 3 кути; 3) 5 кутів.
161. Розгорнутий кут поділили внутрішніми променями на рівні кути. Знайдіть градусну міру цих кутів, якщо отримано:
1) 2 кути; 2) 4 кути; 3) 6 кутів.
162. Кути, що дорівнюють 20° і 60°, мають спільну сторону. Який кут утворює бісектриса більшого кута зі спільною стороною цих кутів? Розгляньте два випадки.
163. У розгорнутому куті AOD проведено внутрішні промені ОВ і ОС. Знайдіть градусну міру кута АОВ, якщо ∠ ВОС = 90° і ∠ АОВ = ∠ COD.
164. У Сергійка вдома годинник із боєм, який відбиває кожну годину. Коли Сергійко прийшов зі школи, кут між стрілками був тупим. Рівно за півгодини годинник пробив. У цей момент кут між стрілками став прямим. О котрій годині Сергійко прийшов зі школи?
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
165. Назвіть приклади прямих кутів та розгорнутих кутів, які можна побачити в класній кімнаті.
166. Визначте кут між напрямками (мал. 93):
1) південь і схід;
2) південь і північ;
3) південь і захід;
4) північ і південний захід;
5) захід і північний захід;
6) схід і північ;
7) схід і північний захід;
8) північний захід і південний схід.
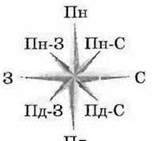
Мал. 93
ЗАДАЧІ НА ПОВТОРЕННЯ
167. Обчисліть усно:
1) (404 – 104): 3 + 12 ∙ 1; 2) (146 + 54): 100 ∙ 9 – 18.
168. Обчисліть:
1) 20 + 1035 : 23 – 595 : 35; 2) 125 ∙ 8 – 36 ∙ 25 + 40 ∙ 15.
169. Складіть задачу за виразом: 650 – (150 + 150 ∙ 2).
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Які числа називаються натуральними?
2. Назвіть найменше натуральне число. Чи існує найбільше натуральне число?
3. Поясніть відмінності між цифрою і числом.
4. Чому нашу систему числення називають десятковою?
5. У чому суть позиційного запису чисел?
6. Назвіть за порядком зростання чотири класи в запису натуральних чисел.
7. Що називається променем? Початком променя?
8. Що називається відрізком? Кінцями відрізка?
9. Що означає знайти довжину відрізка?
10. Як знайти довжину відрізка, якщо відомі довжини його частин?
11. Як порівнюють два відрізки? Які відрізки називаються рівними?
12. Який промінь називається координатним? Як побудувати координатний промінь?
13. Як знайти розміщення точки на координатному промені за ЇЇ координатою?
14. Що називається числовим виразом? Що називається значенням числового виразу?
15. Що називається числовою рівністю? Що показує числова рівність?
16. Що називається числовою нерівністю? Як записують подвійну нерівність?
17. Поясніть, як порівняти два числа за допомогою координатного променя.
18. Як порівняти багатоцифрові натуральні числа?
19. Що називається кутом? Як позначають кути? В яких одиницях вимірюють кути?
20. Для чого слугує транспортир? Поясніть, як виміряти кут за допомогою транспортира.
21. Як побудувати кут заданої градусної міри?
22. Які кути ви знаєте? Назвіть їх градусну міру.
23. Які кути називаються рівними?
24. Що таке бісектриса кута?
25. Як знайти градусну міру кута, якщо відомі градусні міри його частин?
ТЕСТОВІ ЗАВДАННЯ
Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового завдання потрібно 10-15 хв.
1.Оберіть правильний запис числа вісім мільйонів п’ятдесят шість тисяч.
А.8000056. Б. 800 056. В. 8 056 000. Г. 8 560 000.
2. Дано точки А(2), В(8) і С( 10). На якому малюнку точки А, В і С позначено правильно?
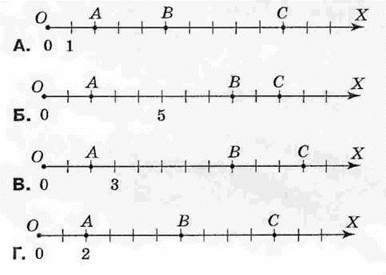
3. Укажіть правильну числову нерівність:
А. 101 < 99. В. 235 550 < 235 509.
Б. З 478 >3 487. Г. 4 215 100 > 4 215 099.
4. Точка К ділить відрізок MN на два відрізки – МК і KN. MN = 40 мм, KN = 3 см. Яка довжина відрізка МК у сантиметрах?
А. 7 см. Б. 10 см. В. 1 см. Г. 43 см.
5. ∠ АОВ = 140°. Промінь ОС – бісектриса ∠ АОВ, а промінь ОК – бісектриса ∠ АОС. Яка градусна міра ∠ КОВ?