ЛІНІЙНА ФУНКЦІЯ
РОЗДІЛ 4 ФУНКЦІЇ
&17. ЛІНІЙНА ФУНКЦІЯ
У дослідженні реальних процесів і явищ функції відіграють особливу роль – математичних моделей. Найбільш важливим функціям математики дають власні назви. Однією з них є лінійна функція. Розглянемо приклади, що приводять до лінійної функції.
Нехай 1 кг цукерок коштує 25 грн. Тоді залежність між масою т цукерок та їх вартістю р можна подати як функцію:
Р = 25m.
Нехай розмір місячної зарплати страхового агента складається з 2000 грн та 10 % від прибутку з продажу страхових полісів. Тоді залежність
S = 0,1k + 2000.
В обох прикладах дістали функцію, яку можна в загальному вигляді задати формулою у = kx + b, де х – незалежна змінна, k і b – деякі числа.
Запам’ятайте!
Функція, яку можна задати формулою виду у = kx + b, де х – аргумент, k і b – деякі числа, називається лінійною функцією.
У цієї функції: область визначення – усі числа, область значень – усі числа.
? Що є графіком лінійної функції? Розглянемо приклад.
Задача 1. Побудуйте графік функції у = 2х + 1.
Розв’язання. Дана функція є лінійною за означенням.
X | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
Y(x) | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
На координатній площині побудуємо точки з координатами (-2,5; -4), (-2; -3), (-1,5; -2), (-1; -1). (-0,5; 0), (0; 1), (6,5; 2), (1; 3), (1,5; 4), (2; 5). Прикладемо лінійку до цих точок. Бачимо, що всі вони лежать на одній прямій (цей факт ви зможете строго довести в старшій школі). З’єднаємо побудовані точки суцільною лінією, тобто проведемо через них пряму. Ця пряма і є графіком даної функції (мал. 31).
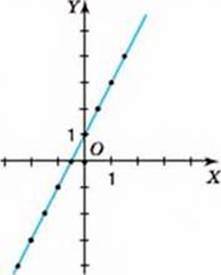
Мал. 31
Запам’ятайте!
Графіком лінійної функції є пряма.
? Скільки значень лінійної функції треба знайти, щоб побудувати її графік? Графіком лінійної функції є пряма. Для її побудови достатньо двох точок. Цей факт вам відомий із курсу геометрії.
Задача 2. Побудуйте графік функції у =3х – 2.
Розв’язання. Дана функція є лінійною. Тому для побудови графіка достатньо побудувати дві його точки. Для цього складемо таблицю значень даної функції для двох довільних значень аргументу (табл. 22).
Таблиця 22
X | 0 | 2 |
Y(x) | -2 | 4 |
На координатній площині позначимо точки з координатами (0; -2) і (2; 4). Проведемо через них пряму. Ця пряма і є графіком даної функції (мал. 32).
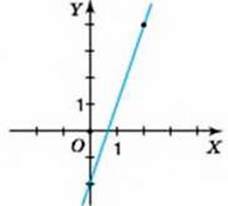
Мал. 32
? Чи можна вважати графіком лінійної функції пряму, перпендикулярну до осі абсцис? Ні. Тому що в точок такої прямої (наприклад, прямої х = 3 на мал. 33) абсциса та сама, а ординати набувають будь – яких значень. Тобто одному значенню х відповідає безліч значень у. Отже, тут немає функціональної залежності. А це означає, що не можна говорити й про будь-який різновид функції зокрема про лінійну функцію.
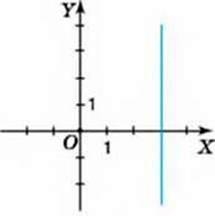
Maл. 33
Запам’ятайте!
Кожна пряма, яка не перпендикулярна до осі абсцис, є графіком лінійної функції.
За допомогою графіка можна з’ясувати не лише область визначення та область значень лінійної функції, а й деякі інші її властивості. Зокрема, за графіком легко побачити, за яких значень аргументу значення функції дорівнює нулю, а за яких – є додатним чи від’ємним. Розглянемо приклад.
Задача 3. На малюнках 34 і 35 зображено графіки функцій у = 2х – 2 і у = -2х + 2. Користуючись графіком, знайдіть усі значення аргументу, за яких значення функції: а) дорівнює нулю; б) є додатним; в) є від’ємним.
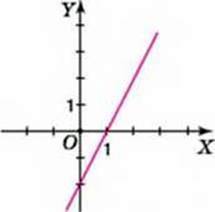
Мал. 34
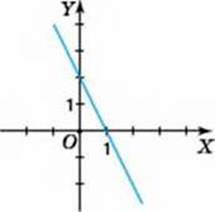
Мал. 35
Розв’язання.
1. За малюнком 34 для функції у = 2х – 2 дістанемо:
A) y = 0. якщо х = 1; б) у > 0, якщо х > 1; в) у < 0, якщо х < 1.
2. За малюнком 35 для функції у = -2х + 2 дістанемо:
А) у = 0, якщо х = 1; б) у > 0, якщо x < 1; в) у < 0, якщо х > 1.
? Як характеризує лінійну функцію число k? Поміркуємо.
Подивіться на малюнки 34 і 35. На першому із цих малюнків графік утворює з додатним променем осі ОХ гострий кут, а на другому – тупий. У функції у = 2х – 2 коефіцієнт k > 0, а у функції у = -2х + 2 коефіцієнт k < 0. Оскільки коефіцієнт h характеризує кут, який графік лінійної функції утворює з додатним променем осі ОХ, то число k так і називають – кутовий коефіцієнт.
Зверніть увагу:
Графік функції y = kx + b утворює з додатним променем осі ОХ:
– гострий кут, якщо k > 0;
– тупий кут, якщо k < 0.
? Як характеризує лінійну функцію число b? Поміркуємо.
Знову звернемося до малюнків 34 і 35. Ви бачите, що графік функції у = 2х – 2 перетинає вісь OY у точці з ординатою -2 (мал. 34), а графік функції у = -2х + 2 перетинає вісь OY в точці з ординатою 2 (мал. 35). Загалом, число b у формулі y = kx + b показує ординату точки перетину графіка лінійної функції з віссю OY.
Зверніть увагу:
Графік лінійної функції у = kx + b перетинає вісь OY у точці:
– з додатною ординатою, якщо b > 0;
– з від’ємною ординатою, якщо b < 0;
– з ординатою, що дорівнює 0, якщо b = 0.
Аналізуючи графіки функції! на малюнках 34 і 35, можна виявити ще й такі властивості даних функцій. На малюнку 34 більшому значенню аргументу відповідає більше значення функції. Отже, функція у = 2х – 2 є зростаючою. У неї k > 0. На малюнку 35 більшому значенню аргументу відповідає менше значення функції. Отже, функція у = -2х + 2 є спадною. У неї k < 0. На малюнку 36 ви бачите приклад особливого випадку лінійної функції, у якої k = 0. Це функція у = 2.
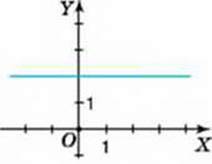
Мал. 36
Зверніть увагу:
Лінійна функція у = kx + b:
– зростає, якщо k > 0;
– спадає, якщо k < 0;
– є сталою, якщо k = 0.
Дізнайтеся більше
Із курсу геометрії ви знаєте, що дві прямі на площині або перетинаються, або паралельні, або збігаються. Те саме можна сказати і про взаємне розміщення графіків двох лінійних функцій. Яким воно є, можна з’ясувати, не будуючи графіків, а аналітично – за формулами, якими задано дані функції.
Нехай дві лінійні функції задано формулами у = k1x + b1 і у = k2x + b2. Щоб з’ясувати, яким є розміщення графіків цих функцій, розглянемо такі випадки.
1. Якщо графіки даних функцій збігаються, то k1x + b, = k2x + b2 за будь-яких значень змінної х. Тоді обидві формули набуватимуть того самого вигляду, якщо k1 = k2 і b1 = b2.
2. Якщо графіки даних функцій паралельні, то їх кутові коефіцієнти мають бути рівними, тобто k1, = k2, а b1 ≠ b2.
Наприклад, на малюнку 37 зображено графіки функцій у = х + 2 i у = х – 2, які є паралельними. У цих функцій k1 = k2 = 1, b1 = 2, b2 = -2.
3. Якщо графіки даних функцій перетинаються, то їх кутові коефіцієнти мають бути різними, тобто k1 ≠ k2. Наприклад, на малюнку 38 зображено графіки функцій у = х + 2 і у = 2х + 2. У них k1 = 1, k2 = 2. Тому вони перетинаються. Щоб знайти точку їх перетину, прирівняємо праві частини відповідних формул: х + 2 = 2х + 2, звідси х = 0. Тоді у(0) = 0 + 2 = 2. Отже, графіки даних функцій перетинаються в точці А (0; 2).
5. Особливим є випадок, коли k1 ∙ k2 = -1. У цьому випадку графіки даних функцій взаємно перпендикулярні. Наприклад, на малюнку 39 зображено графіки функцій у – 2х + 1 і y = -0,5х – 1,
Які є взаємно перпендикулярними. У цих функцій k1 ∙ k2 = 2 ∙ (-0,5) =-1.
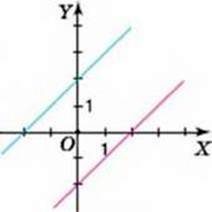
Мал. 37
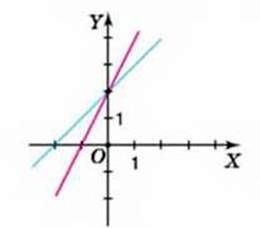
Мал. 38
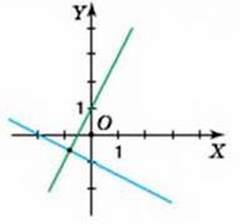
Мал. 39
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Яка функція називається лінійною?
2. Що є графіком лінійної функції?
3. Скільки значень лінійної функції треба знайти, щоб побудувати її графік?
4. Як побудувати графік лінійної функції?
5. За яких значень k лінійна функція y = kx + b є зростаючою; спадною; сталою?
6. Як характеризує лінійну функцію число b?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
882. На якому з малюнків 40-41 зображено графік лінійної функції?
883. Чи є лінійною функція, яку задано формулою:
1)у = 2х2 + х + 1; 2) у = 2 + х3; 3) у = 4 – 5х?
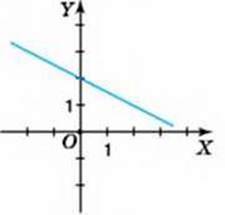
Мал. 40
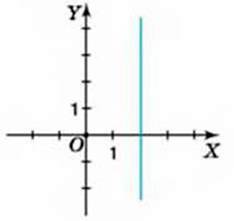
Мал. 41
884. Чи правильно, що графік функції у = х проходить через точку:
1) A (2; 2); 2) В (-2;-4); 3) С (1; 1)?
885. Чи правильно, що дана функція зростає:
1) у = -3х + 3; 2) у = 2; 3)у = 5х – 1?
886. Чи правильно, що дана функція спадає:
1) у = 4х – 3; 2)у = -2; 3)у = -6х + 2?
887. Чи правильно, що дана функція є сталою:
1) у = -3х + 3; 2)у = 4х; 3)у = -0,5?
888. Назвіть кутовий коефіцієнт функції:
1) y = 4х + 5; 2) y = -3 – 6х; 3)у = 4 + 
Х.
889 . Назвіть кутовий коефіцієнт функції:
1)у = 3х – 7; 2) у = -4 – 0,5х; 3)у = 
+ 
Х.
890. Чи правильно, що графік функції у = 4х – 5 перетинає вісь OY у точці:
1) з додатною ординатою;
2) з від’ємною ординатою;
3) з ординатою, що дорівнює 0?
891. Чи правильно, що графік функції у = -5х + 7 перетинає вісь OY у точці:
1) з додатною ординатою;
2) з від’ємною ординатою;
3) з ординатою, що дорівнює 0?
892. Відомо, що графік функції у = kx + b перетинає вісь OY у точці А (0; -3). Яким у такому випадку буде значення b.
1) додатним; 2) від’ємним; 3) рівним нулю?
893. Відомо, що графік функції у – kx + b перетинає вісь ОУ у точці С (0; 1,7). Яким у такому випадку буде значення b:
1) додатним; 2) від’ємним; 3) рівним нулю?
894. Який кут – тупий чи гострий – утворює з додатним променем осі ОХ графік функції:
1)у = 5х – 1; 2)у = 4 + 3х; 3)у = 0,3 – 1,6х?
895. Який кут – тупий чи гострий – утворює з додатним променем осі ОХ графік функції:
1) y = 2x + 2; 2)у = 0,5х – 7; 3) у = 0,8 – 1,2x?
896. На малюнку 42 зображено графік деякої лінійної функції. Користуючись графіком, знайдіть:
1) значення у, якщо х = -1; 0; 1; 2,5;
2) значення х, за якого у = 0;
3) три значення аргументу, за яких значення функції додатне;
4) три значення аргументу, за яких значення функції від’ємне;
5) значення аргументу, за яких функція зростає;
6) значення аргументу, за яких функція спадає.
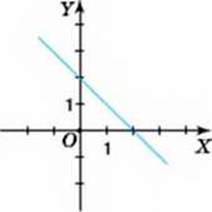
Мал. 42
Мал. 43
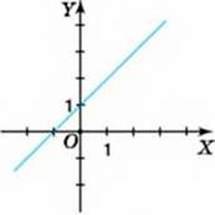
897. На малюнку 43 зображено графік деякої лінійної функції. Користуючись графіком, знайдіть:
1) значення у, якщо х = -1; 0; 1; 2,5;
2) значення х, за якого у = 0;
3) три значення аргументу, за яких значення функції додатне;
4) три значення аргументу, за яких значення функції від’ємне;
5) значення аргументу, за яких функція зростає;
6) значення аргументу, за яких функція спадає.
Maл. 44
Мал. 45
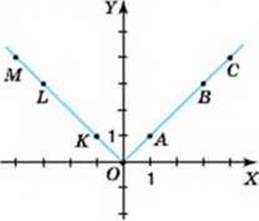
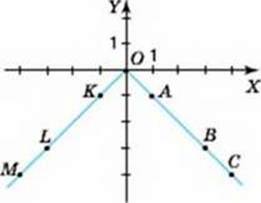
898. На малюнках 44-45 зображено графіки деяких функцій. Серед точок, позначених на графіку, укажіть пари точок:
1) із рівними ординатами. Які в цих точок абциси?
2) із протилежними абцисами. Які в цих точок ординати?
Яку закономірність помітили? Чи задовольняють координати точок кожної пари функцію, задану формулою:
А) у = |х|, 6)у = -|х|?
899. Пара точок із рівними ординатами належить графіку: а) у = |y|; б) у = -|x|. Визначте координати другої точки, якщо одна з них має координати: 1) (-2; -2); 2) (3; 3); 3) (1; -1); 4) (-7; -7); 5) (1,25; 1,25); 6) (4,1; 4,1)?
900. Якому з графіків функцій у = |x| чи у = -|х| належить точка з координатами: 1) (-2; -2); 2) (1; -1); 3) (-1; 1); 4) (-1; -1); 5) (-0,3; 0,3); 6) (1,5; 1,5)?
901. Функцію задано формулою у = 2х – 5. Накресліть у зошиті таблицю 23 та заповніть її.
Таблиця 23
X | -2 | -1 | 0 | 1 | 2 |
Y |
902. Функцію задано формулою у = – x + 3. Накресліть у зошиті таблицю 24 та заповніть її.
Таблиця 24
X | -2 | -1 | 0 | 1 | 2 |
Y |
903 Знайдіть y (-1); y(0), y (2,5), якщо:
1) y =|x – 1| – 1; 3) y = 1 – |1 – x|;
2) y = |x – 1| + 1; 4) у = 1 – |х + 1|.
904. Знайдіть у (-3), у (-1,5), у (0), у (3), якщо:
1) у = |х – 2| – 1; 3) у = 2 – |2 – x|;
2) y = |x – 2| + 1; 4) у = 3 – |х + 2|.
905. Чи належить графіку функції у = 5х – 2 точка:
1)А (1; -3); 2) В (1; 3); 3)С (0; 2); 4)D(-1;-7)?
906. Яка з точок М (-1; -3), N (1; 3), Р (2; 4), R (-2; 0) належить графіку функції у = – х – 2?
907. Назвіть будь-які три точки, що належать графіку функції:
1) у = -2х + 7; 2) у = 0,5х – 1,5.
908. Чи належить графіку функції у = 4 – 3х точка:
1)K(-1; 1); 2) L (1; 1); 3) М(2; 2); 4)N(-2; -10)?
909. Побудуйте графік функції:
1)у = х – 1; 2) у = – х – 1; 3)y = – x + 1; 4)у = х + 1.
910. Побудуйте графік функції:
1) у = 2х + 1; 2)у = -2х + 1; 3)у = -2х – 1; 4) у = 2х – 1.
911. Графік якої з функцій перетинає вісь ординат у точці з додатною ординатою:
1) y = 6х – 5; 3) y = -6х – 5; 5) у = –
Х + 2;
2) y = -6x + 5; 4) у = 
Х – 1; 6) у = -2,6х – 3,5;?
912. Графік якої з функцій перетинає вісь ординат у точці з від’ємною ординатою:
1)у =-7х – 6; 2) у = -7х + 6; 3) y = 7х – 6?
913. У якій точці перетинає вісь ординат графік функції:
1) y = 2x – 3; 2) у = -3х + 9; 3) y = –X +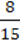 
?
914. У якій точці перетинає вісь абсцис графік функції:
1) y = 3х – 12; 3 )у = –
X –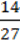 
; 5)y = -6x + 15;
2) у = -7х + 21; 4) y = 5x + 18; 6) y = –
X –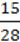 
?
915. У якій точці перетинає вісь абсцис графік функції:
1) у = 4х + 14;
2) у = – 8х + 20;
3)y – –X –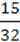 
?
916. Графік функції у = 4х + m проходить через точку М (-2; 8). Знайдіть значення m.
917. Графік функції у = -2,4х + k проходить через точку К (5;-6). Знайдіть значення k.
918. Графік функції у – 6х – а проходить через точку А (-
; -2). Знайдіть значення а.
919. Графік функції у = bх – 1 проходить через точку В (-1; –
). Знайдіть значення b.
920. Графік функції у – ах + 3 проходить через точку А (-2; 1). Знайдіть значення а.
921. Графік функції у = 7 – сх проходить через точку С (-4; -5). Знайдіть значення с.
922. Побудуйте графік функції:
1) y = 0,5х – 1,5; 2) y =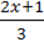 
; 3) y = 
X – .
Користуючись графіком, знайдіть усі значення аргументу, за яких значення функції: а) дорівнює нулю; б) є додатним; в) є від’ємним.
923. Побудуйте графік функції:
1) y = -1,5x + 3; 2) y =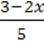 
; 3) y = 1
X + 
.
Користуючись графіком, знайдіть усі значення аргументу, за яких значення функції: а) дорівнює нулю; б) є додатним; в) є від’ємним.
924. Побудуйте в одній системі координат графіки функцій:
1) у = 2х – 0,5 і у = -0,5х + 2; 2) y = –
X + i y = 
+ 3.
Користуючись графіками функцій, знайдіть координати їх точок перетину.
925. Побудуйте в одній системі координат графіки функцій:
1) y = 3x – 1 i y + -2x + 4; 2) y = –X + 
i y = 
– 1.
Користуючись графіками функцій, знайдіть координати їх точок перетину.
926. Знайдіть f(-2), f(-1), f(0), f(1), f(2), якщо:
927. Знайдіть область значень функції:
1) у = х + 1; 2) y = |x|; 3) у = |х| + 2; 4)у = |x| – 3.
928. Знайдіть область значень функції:
1) y = 2х; 2) у = |х| – 5.
929. На малюнках 46-47 зображено графіки деяких функцій.
1. Якому з графіків функцій належить точка з координатами: а) (0; 1); б) (0; -1)?
2. Серед точок, позначених на графіку, укажіть пари точок:
А) із рівними ординатами. Які в цих точок абсциси?
Б) із протилежними абсцисами. Які в цих точок ординати?
3. Укажіть малюнок, на якому позначено пари точок із координатами, що задовольняють функцію, задану формулою:
А) у = |x| + 1; б) y = |x| – 1.
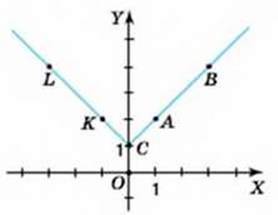
Мал. 46
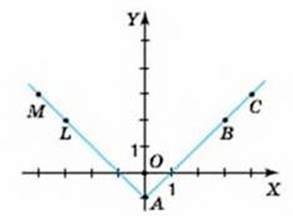
Мал. 47
930. На малюнках 48-49 зображено графіки деяких функцій.
1. Якому з графіків функцій належить точка з координатами: а) (0; 1); б) (0; -1)?
2. Серед точок, позначених на графіку, укажіть пари точок:
А) із рівними ординатами. Які в цих точок абсциси?
Б) із протилежними абсцисами. Які в цих точок ординати?
3. Укажіть малюнок, на якому позначено пари точок із координатами, що задовольняють функцію, задану формулою: а) у = -|х| + 1; б) у = -|х| – 1.
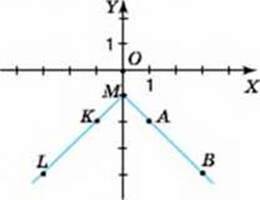
Мал. 48
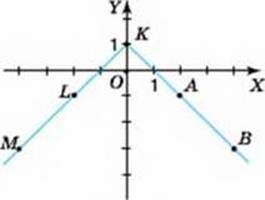
Мал. 49
931. Графік функції у = ах + b проходить через точки А (-1; -3) i В (0; 2). Знайдіть значення а і b.
932. Задайте формулою будь-яку лінійну функцію, графік якої проходить через точку: 1)А (-1; 1); 2)В (5; 5).
933. Графік функції y = kx + b проходить через точку А (-1; -10), а його кутовий коефіцієнт дорівнює НСД чисел 42 і 91. Знайдiть значення k і b.
934. Графік функції у = ах + с проходить через точку В (1; 14), а його кутовий коефіцієнт дорівнює НСД чисел 96 і 112. Знайдіть значення а і с.
935. Побудуйте графік функції:
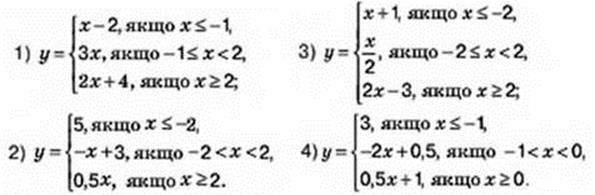
936. Побудуйте графік функції:
1) у = |х| + х;
2) у = |х| – х;
3) у =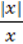 
.
937. Побудуйте графік функції:
1) у = 2 |х + 1| + 5; 3) у= |х – 3| – |1 – х|;
2) y = |х – 1 |+ |х – 2|; 4) у = 2|х – 3| – 3|х + 2|.
938. Побудуйте множину точок, координати яких задовольняють рівняння:
1) |y| = x – 3; 2) |x| + |y| = 1; 2) |x| – |y| = -1.
Чи є отримане зображення графіком функції? Відповідь обгрунтуйте.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
939. На початку тижня мама дала Іринці 50 грн для власних витрат. Щодня дівчинка витрачала по 2 грн 50 к. на проїзд до школи і назад та 5 грн 50 к. на обід. Інших витрат протягом тижня в Іринки не було. Запишіть у вигляді формули залежність суми грошей, що залишилась у дівчинки, від дня тижня. Побудуйте графік отриманої функції.
940. Для пошиття одного робочого халату треба 1,7 погонного метра тканини. Запишіть у вигляді формули залежність загальної кількості погонних метрів тканини від кількості халатів, які треба пошити. Скільки метрів тканини треба, щоб пошити 5, 8, 25, 100 таких робочих халатів?
941. Дві групи піших туристів, вийшовши не одночасно з однієї бази за тим самим маршрутом, мали зустрітися в поході й далі продовжити його разом. Перша група вирушила з бази о 7 год і рухалася зі швидкістю 3 км/год. Друга група вирушила з бази через дві години і рухалася зі швидкістю 5 км/год. Через скільки годин після виходу другої групи вони зустрінуться? Розв’яжіть задачу графічно.
ЗАДАЧІ НА ПОВТОРЕННЯ
942. Знайдіть n, якщо:
1) (25)24 = (25n)4; 3) (2,3)54 = (2,З9)n;
2) (6)48 = (6n)16;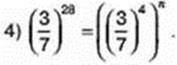 
943. Сума деякого числа, його та 
дорівнює 124. Знайдіть невідоме число.
944. Знайдіть найменше чотирицифрове число, якщо воно ділиться на 2, 5, 9 і його запис містить цифру 3.
945. прямокутнику сторони дорівнюють 10 см і 15 см. Меншу сторону збільшили на 40 %, а більшу – зменшили на 40 %. Як змінився периметр прямокутника (у %)?
(1 votes, average: 5.00 out of 5)
Loading...