Лінійна функція та її графік
Урок № 66
Тема. Лінійна функція та її графік
Мета: сформувати свідоме розуміння учнями взаємозв’язку між взаємним розташуванням графіків двох лінійних функцій та співвідношенням їх кутових коефіцієнтів; виробити вміння: за даними рівняннями лінійних функцій робити висновки щодо взаємного розташування графіків; знаходити аналітичним способом координати точки перетину графіків двох лінійних функцій.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний момент
1. Перевірка готовності учнів до
2. Учні-консультанти повідомляють про стан виконання домашнього завдання.
II. Перевірка домашнього завдання (зібрати зошити)
Бліц-тест
1. Яка з формул задає лінійну функцію:
1) у = 7х – 0,5;
2) 
;
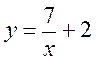3) 
;
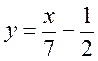4) у = 7х;
5) у = 7х2 + 2.
Варіанти відповіді:
А. 1; 2; 3; 4. Б. 1; 3; 4. В. 1; 3; 4; 5. Г. Усі.
2. Графік лінійної функції проходить через точку (0; 0) та точку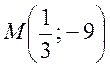 
. Задайте її формулою.
Варіанти відповіді:
А. у = -27х. Б. у = 27х. В. у = 3х. Г. у = -3х.
3. Яким з рівнянь може бути задана [лінійна] функція, графік якої зображено на рисунку:
А. у = х – 2.
Б. у = х + 2.
В. у = 2х.
Г. у = 2.
4. В яких точках перетинає графік у = х – 7:
А) вісь Оу; б) вісь Ох?
A. а) (0; 7); б) (7; 0).
Б. а) (0; -7); б) (-7; 0).
B. а) (0; 7); б) (-7; 0).
Г. а) (0; -7); б) (7; 0).
III. Робота з випереджальним домашнім завданням
@ Організуємо так: 1) перевіряємо, які графіки побудували учні (учні “презентують” свої роботи; коригують їх); 2) за алгоритмом порівняння здійснюємо порівняння (а) формул, б) графіків) та робимо висновки щодо виконаних завдань та формулюємо загальну гіпотезу.
IV. Формулювання мети й завдань уроку
Учитель разом з учнями формулює навчальну мету уроку (див. мета).
V. Актуалізація опорних знань
Виконання усних вправ
1. Обчисліть: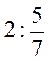 
; 
; 
; 
; 
; 
.
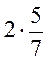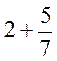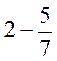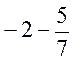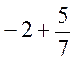2. Розв’яжіть рівняння:
1 + x = 1 – х; 9х – 4 = 9x + 5; 3x + 1 = 1,5 – х.
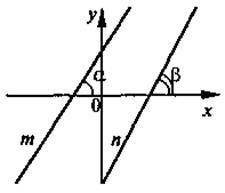
3. Що можна сказати про прямі m і n (див. рис), якщо кути? і?: а) рівні; б) нерівні?
4. Чи проходить графік функції у = -0,25х + 4 та у = х – 1 через точку А(4; 3)? Що можна сказати про взаємне розташування цих графіків?
VI. Вивчення нового матеріалу
@ Основну мету уроку – формування свідомого розуміння змісту взаємозв’язку між співвідношенням коефіцієнтів k1 і k2 у рівняннях лінійних функцій y = k1x + b1 та y = k2x + b2, ми проводимо індуктивним методом (випереджальне домашнє завдання тому підтвердження), тому ця частина зводиться до перекладу висновків, здобутих під час перевірки виконання домашнього завдання математичною мовою, а саме:
1) якщо лінійні функції y = k1x + b1 та y = k2x + b2 мають k1 = k2,а b1 ? b2, то графіки цих лінійних функцій паралельні;
2) якщо в рівняннях y = k1x + b1 та y = k2x + b2, що задають лінійні функції k1 ? k2, то графіки таких лінійних функцій перетинаються.
Єдине, на що треба звернути увагу – як знайти точку перетину графіків двох лінійних функцій. Для усвідомлення відповідного алгоритму, проведемо бесіду за планом:
1) Що означає вислів “Дві прямі перетинаються”? Що можна сказати про точку перетину?
2) Якщо y = k1x + b1 – лінійна функція і координати точки А(хА; уА) перетворюють це рівняння на правильну рівність, що це означає?
А якщо координати цієї ж самої точки перетворюють рівняння y = k2x + b2 на правильну рівність, що це означає?
3) Точка А(хА; уА ) належить графікам y = k1x + b1 та y = k2x + b2. Яких значень будуть набувати вирази (k1x+b1) та (k2x+b2), якщо х = хА?
4) Відомо, що y = k1x + b1 та y = k2x + b2 – лінійні функції, графіки яких перетинаються в даній точці. Яких значень набувають ці функції при значенні аргументу, що дорівнює абсцисі цієї точки? Як це записати мовою математики?
Після такої бесіди більшість учнів усвідомлює зміст переходу від геометрично заданих функцій (функції як прямі) до аналітичного змісту умови перетину їх графіків. Результати обговорення бажано записати в зошити.
Конспект 20 |
Взаємне розташування графіків двох лінійних функцій |
|
VI. Первинне закріплення знань. Вироблення вмінь
Виконання усних вправ
1. Чи перетинаються графіки функцій? Чому?
1) у = 8х – 11; у = 5х – 10; 2) у = 8х – 11; у = 5х – 11;
3) у = 8х – 11; у = 8х – 10; 4) у = 8х; у = -8х.
2. Серед функцій: у = x + 0,5; у = -0,5х + 4; y = 5x – 1; y = 0,5x + 1;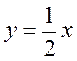 
виділіть ті, графіки яких паралельні графіку функції у = 0,5х + 4.
3. Яка лінійна функція має графік, що паралельний до графіка функції у = 1,3х – 7 і проходить через початок координат?
Виконання письмових вправ
1. Знайдіть координати точок перетину графіків функцій:
1) у = 10х – 8; та у = -3х + 5;
2. 2) у = 14 – 2,5х та у = 1,5х – 18;
3) у = 20х – 70 та у = 70х + 30;
4) у = 37х – 8 та у = 25х + 4;
5) у = 14х та у = х + 26;
6) у = -5х + 16 та у = -6.
3. Дано лінійну функцію у = 2,5x + 4. Задайте формулою таку лінійну функцію, щоб її графік:
1) був паралельний до графіка цієї функції;
2) перетинав графік цієї функції і проходив через початок координат;
Перетинав графік цієї функції в точці перетину даного графіка з віссю Оу.
4. Покажіть схематично взаємне розташування на координатній площині графіків функцій:
1) у = 17х та у = 17х – 20;
2) у = -30х та у = -30х + 8;
3) у = 3х – 2 та у = -3х – 2.
VII. Підсумок уроку (“Аукціон” або вікторина)
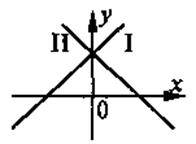
На рисунку зображено графіки 2-х лінійних функцій (І, II). Які висновки щодо k та b ви можете зробити?
VIII. Домашнє завдання
№ 1. Повторіть зміст основних понять теми (див. конспект). Складіть питання до вікторини за темою “Функція”.
№ 2. Чи перетинаються графіки функцій:
1) у = 6х + 9 та у = 2х – 7;
2) у = -0,5х + 2 та у = 2,5х – 10;
3) у = 0,2х – 9 та у =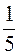 
Х + 1;
4) у = х та у = -3х + 3,4?
Для графіків, що перетинаються, знайдіть координати точки перетину.
№ 3. Задайте формулою лінійну функцію, графіком якої є пряма, що проходить через точку А (2; 3) і паралельна до графіка функції у = 1,5х – 3. Побудуйте її графік.
(1 votes, average: 5.00 out of 5)
Loading...