МНОГОЧЛЕН ТА ЙОГО СТАНДАРТНИЙ ВИГЛЯД
РОЗДІЛ 3 МНОГОЧЛЕНИ
У розділі дізнаєтесь:
► що таке многочлен;
► який вигляд многочлена називають стандартним;
► що називають степенем многочлена;
► які властивості дій з многочленами; про формули скороченого множення;
► як розкладати многочлен на множники;
► як застосувати вивчений матеріал на практиці

&8. МНОГОЧЛЕН ТА ЙОГО СТАНДАРТНИЙ ВИГЛЯД
Запишемо суму одночленів х2, -15ху, 4×5у2, -3, -5х5у2. Дістали вираз, що містить п’ять доданків:
Х2 + (-15xy) + (4x5y2) + (-3) + (-5х5y2).
Такий
Вираз, що є сумою кількох одночленів, називається многочленом.
? Чи є многочленом різниця одночленів? Так, оскільки дію віднімання завжди можна замінити дією додавання:
7х – 2 = 7х + (-2).
Задача 1. Чи можна перетворити у многочлен вираз:
1)3 : (5х3 – у2);
2) 3(5х3 + y2)?
Розв’язання. 1. Вираз 3 : (5х3 – у2) не є цілим, оскільки містить ділення на вираз зі змінними. Тому його перетворити у многочлен не можна.
2. Вираз 3(5х3 + у2) можна перетворити в суму одночленів. Розкривши дужки, дістанемо вираз 15х3 + 3у2, який є многочленом.
Многочлени
Розглянемо многочлен х2 – 15ху + 4х5у2 – 3 – 5х5у2. Його третій і п’ятий члени 4х5у2 і -5х5у2 мають ту саму буквену частину х5y2. Це подібні члени многочлени. їх можна звести як подібні доданки у виразі:
4х5у2 – 5х5у2 = – х5у2.
Після зведення подібних членів даний многочлен міститиме не п’ять, а чотири члени, тобто набуде більш простого вигляду:
Х2- 15xy + 4x5y2 – 3 – 5x5y2 = х2 – 15ху – х5у2 – 3.
В отриманому многочлені кожен член є одночленом стандартного вигляду і він не містить подібних членів. Вважають, що такий многочлен записано в стандартному вигляді.
Зверніть увагу:
Щоб звести многочлен до стандартного вигляду:
1) подайте кожен член многочлена в стандартному вигляді;
2) зведіть подібні члени многочлена.
Знайдемо степінь кожного члена многочлена х2 – 15ху – х5у2 – 3. Члени х2 і -15хy мають степінь 2, член – х5у2 має степінь 7. Член -3 – це вільний член многочлена. Степінь вільного члена многочлена дорівнює нулю. Найвищий степінь має член – х5y2. Томy його називають старшим членом даного многочлена. Степінь многочлена визначають за степенем його старшого члена.
Запам’ятайте!
Якщо многочлен подано в стандартному вигляді, то степенем цього многочлена називається степінь його старшого члена.
Задача 2. Знайдіть степінь многочлена:
1) х2 – 15ху – х5у2 – 3;
2) х3y2 – х2у3.
Розв’язання. 1. Старшим членом многочлена х2 – 15 ху – х5у2 – 3 є член – х5у2. Його степінь дорівнює 7. Тому степінь многочлена дорівнює 7.
2. Многочлен х3у2 – х2у3 має два члени однакового степеня 5. Отже, даний многочлен є многочленом п’ятого степеня.
Зверніть увагу:
Щоб визначити степінь многочлена, знайдіть степінь кожного його члена та з’ясуйте, який із них є найбільшим.
Знайшовши степені членів многочлена, його можна упорядкувати за степенями членів. Для цього члени многочлена можна розмістити, наприклад, у порядку спадання їх степенів, починаючи запис зі старшого члена многочлена і закінчуючи його вільним членом, якщо він є:
Х2 – 15ху – х5у2 – 3 = – х5y2 + х2 – 15ху – 3.
Дізнайтеся більше
1. Серед многочленів виділяють особливі види многочленів, які знайшли широке застосування в математиці.
Симетричний многочлен – многочлен від п змінних (n – натуральне число), що не змінюється за будь-яких перестановок змінних. Наприклад: -43ху + х5у2 + х2у5, х2 – 9 + у2.
Справді, якщо в цих многочленах замінити х на у, а у на х, то дістанемо такий самий многочлен.
2. У математиці користуються поняттям алгебраїчної суми, яке об’єднує два поняття – “сума” і “різниця”. Це пов’язано з тим, що різницю можна подати як суму: a – b = a + (-b).
Алгебраїчна сума чисел – це числовий вираз, який містить лише суму (різницю) чисел. Наприклад, 2 + 5 – 6 + 7 – 8 – алгебраїчна сума чисел 2, 5, -6, 7, -8.
Многочлен можна визначити як алгебраїчну суму одночленів. Наприклад, х2 – 2х + х3 – 4 – алгебраїчна сума одночленів х2, -2х, х3 і -4.
3. Митропольський Юрій Олексійович (1917-2008) – видатний математик, академік Національної академії наук України, заслужений діяч науки УРСР, лауреат Державної премії України в галузі науки й техніки, Герой України. Народився в с. Чернишівка Шишацького p-ну Полтавської обл.
З 1951 р. Ю. О. Митропольський працює в Інституті математики НАН України, з яким пов’язана вся його подальша наукова діяльність. Наукову роботу вчений успішно поєднував з педагогічною – на механіко-математичному факультеті Київського університету. Він є автором понад 750 наукових праць. Серед його учнів – 25 докторів і 100 кандидатів фізико-математичних наук.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке многочлен?
2. Які члени многочлена називають подібними?
3. Як звести многочлен до стандартного вигляду?
4. Який член многочлена називають старшим?
5. Що називається степенем многочлена?
6. Як визначити степінь многочлена?
7. Як упорядкувати многочлен за степенями його членів?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
372. Який із даних виразів є многочленом:
1) 3а2 ∙ х3; 3) х3 + х12; 5)5 : х3;
2) 2  – х; 4) 43 + (х + 2,5); 6)
– х; 4) 43 + (х + 2,5); 6) + 5х?
+ 5х?
373. Назвіть одночлени, сума яких є многочленом:
1)4х + 3;
2)5х6 + х6 + х;
3)6х + 4 + х3 + 2х2.
374. Запишіть двочлен, що є сумою одночленів:
1)х2 і х; 2) 2х і 6; 3)4х і 6х; 4)а2 і а3.
375. Запишіть тричлен, що є сумою одночленів:
1) х2, х і 5; 2) х, 4х і 2х; 3) х3, у3 і z3.
376. Чи правильно виділено подібні члени многочлена:
1) а2 + 2х2 + 2а + 2х + х;
2) а2 + х2+ а + х + х;
3) а2 + х2 + а + х + х?
377. У якому випадку правильно зведено подібні члени многочлена – х2 – х + 1 + 2Х2 + 3Х + 4 + 2Х:
1) -2х2 – 3х + 5;
2) Х2 – Х + 5;
3) Х2 – 5Х + 5;
4) Х2 + 4Х + 5?
378. Чи є старшим членом многочлена х3 + 5х2 + 4х + х5 + 3 вираз:
1) х3; 2) х6; 3)5х2; 4)3; 5)4х?
379. Який із даних многочленів записано в стандартному вигляді:
1) х2 + 3х + х2 + 2;
2) х ∙ х + 5х + 2;
3) 2×2 – 2х3;
4) -3х – х2?
380. Чи можна згорнути в одночлен многочлен:
1)3 + 4х + 3х; 2)х2 + х2; 3)3х + 5х + 4х?
381. Назвіть одночлени, які складають многочлен:
1) х – 7;
2)-х – х9 +10х;
3) 6х – 2 – 2у2;
4) 4 – 3n3m + n2 – 5mn3.
382. Назвіть одночлени, які складають многочлен:
1)7ас – 9а – 4; 3)-а – 0,6с – 2с2;
2)6х12 – х + у; 4)-а5с + у2 – 5с5а – 55.
383. Запишіть многочлен, що є сумою одночленів:
1)4а2 і-аb;
2)-2, 3ху,- х2 і х5у2;
3)-5х8, -4х4 і 8.
384. Запишіть многочлен, що є сумою одночленів:
1) 4m2, mn і – рmn;
2) 0,25х2у, -2,8×5 і – ху3;
3) -5, с2а3 і с3а2.
385. Зведіть подібні члени многочлена:
1) 6n + 8,2n – 5,9n – 0,3n + 7;
2) х2 + 3х – 4х2 + 2х;
3)-ас + а2 – са + 3а5 + 2са;
4) 4,5хy – 6х4 – 5 ху – 0,4х4у + ху.
ху – 0,4х4у + ху.
386. Зведіть подібні члени многочлена:
1) -5х + 11 х – 4х + 9х;
2)3,8 – 7х2 + 3,4 – 4х2 – 3х2;
3)-5m2 – 5m + 1 + 2m2 + 9 + 2m;
4) – a2 + 4с2 + 3а2 – с2a2 + 4а3 – 2а2.
387. Який із даних многочленів записано в стандартному вигляді:
1)х2 + 3х + 5х2 + 2; 3) 2х2уz – 2ух3z;
2)у2 + 5у + 2 + х; 4) (-3ху)2 – х2х3?
388. Запишіть у стандартному вигляді многочлен:
1)хх2 + у2+  Х5 + (-0,5х5);
Х5 + (-0,5х5);
2) 100 + p2 + 1,4р – 1,2р2 + 0,6р – 28;
3) -4 + 32аb2а + аb2 + 5 – 3аb + а2b2.
389. Запишіть у стандартному вигляді многочлен:
1) – ух2 + хуу + 3х2 – 8уух;
2) 0,5b + 8 + (-с)3 + 3bc –  Bс – 5 – 6,5b + 7с3.
Bс – 5 – 6,5b + 7с3.
390. Чи правильно, що старшим членом многочлена 81а3 + 25b2 + 3а – b5 є вираз:
1) 81а3; 2) 25b2; 3) 3а; 4) b5; 5) – b5; 6) 81?
391. Знайдіть степінь многочлена:
1)1 + х;
2)4 + 3х;
3)1 + х + х2;
4)-2 + 7х + 5х2.
392. Знайдіть степінь многочлена:
1) 50 + ab;
2)-50 + a + b;
3)-27 – 27а7b7 + а8.
393. Упорядкуйте за степенями членів многочлен:
1)2 + 4а + 6а8 + 1,8а5 + За2 – 2а10 – а4;
2)ху2 + 19х2 + 3ху + 3ху3;
3)1,6аb + 2 B2а2 – 2b3a3 + 3,7;
B2а2 – 2b3a3 + 3,7;
4)7х4 +  Х5 – х3 – 10х2 – 76.
Х5 – х3 – 10х2 – 76.
394. Дано многочлен 2xy – 3х – ху2 – 8x4y + 5. Запишіть:
1) одночлени, які складають многочлен;
2) вільний член многочлена;
3) степінь многочлена;
4) многочлен, упорядкувавши за степенями його члени.
395. Дано многочлен -9 + m + 3mn5 – m2 – 8mn6. Запишіть:
1) одночлени, які складають многочлен;
2) вільний член многочлена;
3) степінь многочлена;
4) многочлен, упорядкувавши за степенями його члени.
396. Зведіть подібні члени многочлена:
1) 7 ху2 + 7х2у – 4ух2 + 4ху2 + ху – х2у;
2) 10a2 – 7а – 3b2 – 3a + (-4а ) – 21 а2 – 4а + 2,1 b2 – 2 + (-5а2);
3) 14m – 3n3 – 2m – Зn2 – 54m + 4n3 + (-n)3 – n3 + m2 + 3n2.
397. Спростіть многочлен -0,5b – 4a3b2 + (2b)2a3 +  B + a + (-0,5)2b та знайдіть значення отриманого виразу, якщо:
B + a + (-0,5)2b та знайдіть значення отриманого виразу, якщо:
1) a = 2 , b = –
, b = – ;
;
2)a =-0,4, b = -1 .
.
398. Запишіть у стандартному вигляді многочлен:
1)-(yz)2 + xy2 + x10x – уух;
2) (а2)4 + 0,3(а2)3 + 5(а4)2 + 0,7 (а2)3 – а6;
3) у 121,1y – 6((-у)4)3 – (y2)5(y3)5 – (-11у)2+ (у6у5)2y3;
4) 5 (х2)2 +
(х2)2 +  (х3х5а2) – 0,4х4 + (-0,125х10) + 81;
(х3х5а2) – 0,4х4 + (-0,125х10) + 81;
5) 4у2y6 + 4 + (-23 )2((-0,5y)3)3 – (2у2)4.
Який степінь отриманого многочлена?
399. Запишіть у стандартному вигляді многочлен:
1) 10,1(у2)2 + 6,9ху2 +  У8 + (-0,125уу7);
У8 + (-0,125уу7);
2) (3k8)3 – 0,01(2k3k)6 – k3 – 1,2k2 + 0,6 kkk;
3) – а2b6 + (-3а)3 + (-0,4b2а2)2b2 –  B – 2,4b + 3а3;
B – 2,4b + 3а3;
4) – х(0,3ух)2 + 32ху2 + х10хy2 – 18уух;
5) 0,4 zxy2z + (-3ху)2 – х2х3 – 1,5z2(- х)(-у)2 + х5.
Який степінь отриманого многочлена?
400. Визначте знак старшого члена многочлена:
 х(-у)3 + хх + (-z)5(-у)8 – 0,5уху2 – 0,5 + (-yz)5(-y)3+ (-х)2.
х(-у)3 + хх + (-z)5(-у)8 – 0,5уху2 – 0,5 + (-yz)5(-y)3+ (-х)2.
401. Спростіть вираз 0,24х4у16 + z2x4уz7 + 2хz2x4y2 – 0,03(у8)2(2х2)3 – 0,8(zyx2)2 – z9у(-х2)2 та упорядкуйте отриманий многочлен за степенями його членів.
402. Спростіть вираз х х (x2)5 – 6((-х)4)3 – (х2)5 (-х3)5 – (-10х)3 + ((х3)5 х2х4)2 – х25 та упорядкуйте отриманий многочлен за степенями його членів.
403. Запишіть суму одночленів -2,6, 3ху2, х8, – х2, 100х3y2, -2х8, 4х4у2 і x8. Упорядкуйте многочлен за степенями його членів. Який степінь отриманого многочлена?
404. Скільки різних двочленів і тричленів можна утворити з одночленів 10а3с, 6 ху, а3 і 7?
405. Подайте многочлен 5х2 – х + 6у вигляді суми чотирьох одночленів, один з яких дорівнює:
1) 5х; 2) 6х; 3) 10.
406. Подайте многочлен х2 + 3х – 10, у вигляді суми чотирьох одночленів, один з яких дорівнює:
1) 2х; 2) – х; 3) 3.
407. Скільки многочленів, які у стандартному вигляді складаються із шести членів, можна утворити додаванням одночленів 10а3, b, 6ху, -10ас, 10а, -3bс і 5? Запишіть ці многочлени.
408. Дано одночлени: 10а, 6ху, а3 і 5. Утворіть многочлен, старший член якого дорівнює:
1) 10а; 2) 6ху; 3) 5; 4) а3.
409. Дано одночлени: 10х2у4, 6ху, 0,02х3, -10у, 4,5х2у2, -5,4, а, і 3х4. Утворіть многочлен, степінь якого дорівнює:
1) 7; 2) 6; 3)4; 4)3; 5)1; 6) 0.
410. Знайдіть суму двох чисел, одне з яких дорівнює k % числа 48, а друге – d% числа 100.
411. Знайдіть суму двох чисел, одне з яких дорівнює 40 % числа А, а друге – 20 % числа d.
412. Відстань від Києва до Харкова на 329 км більша за відстань а км від Києва до Чернігова. Складіть вираз для знаходження довжини шляху Чернігів – Київ – Харків. З’ясуйте, яка відстань між містами Київ і Чернігів, та обчисліть значення складеного виразу.
413. Кожна сторона шестикутника дорівнює а. Одну його сторону збільшили у 2 рази, другу – у 3 рази, третю – у 4 рази і т. д. Знайдіть периметр отриманого шестикутника.
414. Стoрони а і с прямокутника зменшили відповідно на 10 % і на 20 %. Знайдіть периметр отриманого прямокутника. Відповідь запишіть у вигляді многочлена.
415. Cпростіть вираз:
1) (2b ∙ 3bnban )2 + (-4b)3(b2)n ∙  a2nb + a2b3n;
a2nb + a2b3n;
2) an+3an+2 + b3an+2 + b 
3) (-1)n(an)n + (аn)n + 1;
4)(-2b2)n(0,125а2)n(2с)2n + (аbс)2n.
Знайдіть степінь многочлена, у який перетвориться даний вираз після спрощення.
416. Скільки різних многочленів стандартного вигляду можна утворити з одночленів 10а3, 6ху, а3 і – z9?
417. Спростіть вираз (bа5)2n + ba6a10 + а2b8а8nа4n – b(а8)2 + b3nbnс3a8nс2 та упорядкуйте отриманий многочлен за степенями його членів.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
418. Початкову ціну а грн за 1 кг крупи знизили на 10 %, а початкову ціну b грн за 1 кг цукру знизили на 5 %. На скільки зменшиться загальна вартість 4 кг цукру і 8 кг крупи після знижки? За умовою задачі складіть вираз, спростіть його та обчисліть, якщо а = 12, b= 10.
419. На першу клітинку шахової дошки поклали k зерняток, на другу – у k разів більше, ніж на першу, на третю – у k разів більше, ніж на другу і т. д. Скільки зерняток буде на: 1) шести клітинках; 2) десяти клітинках? Відповідь запишіть у вигляді многочлена.
ЗАДАЧІ НА ПОВТОРЕННЯ
420. Перетворіть у десятковий дріб:
1)  ; 2) 2
; 2) 2 ; 3)
; 3) 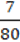 ; 4) 1
; 4) 1 .
.
421. Марійка задумала деяке число, яке збільшила спочатку на 2  , а потім – ще у 3 рази. У результаті отримала 6
, а потім – ще у 3 рази. У результаті отримала 6  . Яке число задумала Марійка?
. Яке число задумала Марійка?