Одночлен. Стандартний вигляд одночлена
Розділ 1. ЦІЛІ ВИРАЗИ
& 5. Одночлен. Стандартний вигляд одночлена
Розглянемо вирази 7; –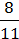 
; а9; – b; 7b2m; 4а2 ∙ (-5)ас.
Це – числа, змінні, їх степені і добутки. Такі вирази називають одночленами.
Вирази а + b2; с3 – 5m; 0,9а2 : m не є одночленами, оскільки містять дії додавання, віднімання, ділення.
Спростимо одночлен 4а2 ∙ (-5)ас, використавши переставну і сполучну властивості множення:
4а2 ∙ (-5)ас = 4 ∙ (-5)а2ас = 20а3с.
Звівши одночлен 4а2 ∙ (- 5)ас до вигляду -20а3с. кажуть, що звели його до стандартного вигляду.
До
Очевидно, що до стандартного вигляду можна звести будь-який одночлен.
Числовий множник одночлена, записаного в стандартному вигляді, називають коефіцієнтом цього одночлена.
Наприклад, коефіцієнтом одночлена 20а3с с число 20, a коефіцієнтом одночлена –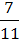 
B9 – число .
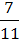Коефіцієнтом одночлена c2d є 1, оскільки c2d = 1 ∙ c2d, а коефіцієнтом одночлена – р7 є -1, оскільки – р7 = -1 ∙ р7. Тобто замість коефіцієнта -1 записують лише знак мінус, а коефіцієнт, що дорівнює 1, взагалі не записують.
Для
Наприклад, одночлен 4а2b7с3 – одночлен дванадцятого степеня, оскільки 2 + 7 + 3 = 12; m7n – одночлен восьмого степеня, оскільки 7 + 1 = 8; -5а4 – одночлен четвертого степеня; 5m – одночлен першого степеня. Одночлен -7 не містить змінних, тому є одночленом нульового степеня.
Який вираз називають одночленом? Який вигляд одночлена називають стандартним виглядом? Наведіть приклад одночлена стандартного вигляду та назвіть його коефіцієнт. Що називають степенем одночлена?
141. (Усно) Які з виразів є одночленами:
1) 3,7х2у;
2) -0,13mpk;
3) х2 – 5;
4) d ∙ (-0,7);
5) x2xt;
6) (- 
р + 9)m;
7) а – b;
8) t11 : t3;
9) 4(х + у)7;
10) – q;
11) -0,7;
12) 0?
142. (Усно) Назвіть одночлени стандартного вигляду та їх коефіцієнти:
1) 4ху;
2) -5aba;
3) 7m2nm3n;
4) – а7b9;
5) 0,3р ∙ 3m;
6) 2аbс;
7) а9b7;
8) 14.
143. Які з виразів є одночленами? Серед одночленів укажіть ті, які записано у стандартному вигляді:
1) 5m ∙ 2р;
2) – 8а2b;
3) х2 + х + 1;
4) m ∙ mk ∙ 5;
5) ( p – 1) ∙ 8;
6) – а2;
7) 17 + а;
8) -129;
9) с18;
10) 2(а – b)2;
11) 1 : с;
12) – abcd.
144. Зведіть одночлен до стандартного вигляду, укажіть його коефіцієнт і степінь:
1) 7а2а3а;
2) 8 ∙ а ∙ 0,1m ∙ 2р;
3) 51 ∙ (-4at);
4) -1 
m4 ∙ 12m2р;
5) -5а2 ∙ 0,2аm7 ∙(-10m);
6) t3 ∙ (-р)7 ∙ t.
145. Зведіть одночлен до стандартного вигляду, вкажіть його коефіцієнт і степінь:
1) -7m2b > ∙ 8mb2;
2) 5m ∙ 2а ∙ ( 36);
3) -7а ∙ (-5а2);
4) -2,2а2 ∙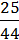 
а3р;
5) – а ∙ (-0,2а2р) ∙ (-0,3р4);
6) c5 ∙ (-а) ∙ (-с4а) ∙ а7.
146. Знайдіть значення одночлена:
1) 3,5а2, якщо а =4; 0,1;
2) -4m3, якщо m = 0; -1;
3) 10xy, якщо х = 1,4, у = -5;
4) -0,01а2 с, якщо а = 5, с = -2.
147. Обчисліть значення одночлена:
1) 1,6а2, якщо а = -5; 0; -1;
2) 5b2с, якщо b = 0,2 і с = 0,1; b = -0,4 і с = 2.
148. Заповніть таблицю у зошиті:
А | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
4 а2 | |||||||||||
-2а2 |
149. Знайдіть:
1) значення х, при якому значення одночлена 0,8 х дорівнює 0; 1; -1; 12;
2) значення а і b, при яких значення одночлена 15ab дорівнює 10; – 60; 0.
150. Знайдіть:
1) значення а, при якому значення одночлена 0,6а дорівнює 0; -3; 12; -300;
2) пару значень х і у, при яких значення одночлена 12ху дорівнює 15; -120; 0.
151. (Усно) Чи є правильним твердження? У разі позитивної відповіді, обгрунтуйте її, якщо відповідь негативна наведіть приклад, що спростовує твердження.
1) Одночлен 7m2 при будь-яких значеннях m набуває додатних значень;
2) одночлен –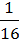 
р4 при будь-яких значеннях р набуває невід’ємних значень;
3) одночлен -12а2 при будь-яких значеннях а набуває від’ємних значень;
4) одночлен 8b3 при будь-яких значеннях b набуває додатних значень.
152. Знайдіть об’єм прямокутного паралелепіпеда, висота якого дорівнює x см, ширина у 3 рази більша за висоту, а довжина у 2 рази більша за ширину.
153. Ширина прямокутника дорівнює b дм, а довжина втричі більша за ширину. Знайдіть площу прямокутника.
Вправи для повторення
154. Розкрийте дужки і спростіть вираз:
1) 3(12х – 5) + 4х;
2) 7(а – 1) – 7а + 13;
3) 4,2 (х – у) + 3,5 (х + у);
4) 12 – 5(1 – х) – 5х.
155. Серед виразів 3( у – х), -3(х – у), -3х – 3у, -3х + 3у знайдіть ті, що тотожно рівні виразу 3у – 3х.
Цікаві задачі для учнів неледачих
156. Задача Степфордського університету. Щоб пронумерувати всі сторінки книжки, друкар використав 1890 цифр. Скільки сторінок у цій книжці?
цифрами, ділиться на 4.
(4 votes, average: 3.00 out of 5)
Loading...