Множення двох багаточленів
Урок № 36
Тема. Множення двох багаточленів
Мета: продовжувати формувати навички: 1) виконання дії множення двох багаточленів та перетворення цього добутку в багаточлен стандартного вигляду; 2) використання названого алгоритму в комплексі з іншими перетвореннями багаточленів, вивчених раніше.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
І. Перевірка домашнього завдання
@ Оскільки від того, чи засвоїли учні алгоритм та способи дій застосування алгоритму перетворення добутку двох багаточленів у багаточлен стандартного
Математичний диктант (із самоперевіркою та корекцією)
Варіант 1 [2]
1. Укажіть багаточлени, які утворюються, якщо кожний їх член 3х-2 [3-2y] помножити на кожний член багаточлена 5-6х2 [2y-1].
2. Помножте багаточлен х + 1 [х – 1] на багаточлен х – 3 [х + 3].
3. Подайте у вигляді багаточлена стандартного вигляду добуток двочлена х – у [a +b] на тричлен х2 + ху + у2 [a2 – ab + b2].
4. Помножте багаточлен х – у [a + b] на багаточлен x + y [a – b].
II. Робота з випереджальним домашнім завданням
Усне опитування
1. Дайте означення степеня числа з натуральним показником п. Що називається основою? показником? Який зміст цих понять?
2. Яку основу і який показник мають степені: а7 ; 53; (-5)n; (2а)n; (2 + а)2; (а + b + с)4?
Як подати ці степені у вигляді добутку?
3. Як подати у вигляді добутку степені: (а + b)2; (а – b)2; (а + b)3; (а – b)3; (а + b)4; (а – b)4?
Яке перетворення можна виконати з утвореними добутками?
Висновок. За правилом (алгоритмом) множення двох багаточленів у багаточлен стандартного вигляду можна перетворювати:
1) добуток двох (і більше) багаточленів;
2) 2-й (і вище) степінь багаточлена, перетворивши спочатку степінь у добуток;
3) якщо у виразі є інші дії над багаточленами, окрім множення двох (і більше) багаточленів (або їх степенів), то дії з перетворення такого виразу у багаточлен стандартного вигляду виконуються за відомими з початкових класів правилами виконання дій.
III. Застосування вмінь та навичок
@ Навіть якщо в учнів закріплено знання алгоритму множення двох багаточленів, не дозволяємо учням нехтувати докладними письмовими записами, особливо, коли йдеться про уведення перетворення виразів, де добуток багаточленів стоїть після знака “-” (після відпрацювання цього моменту й формулювання висновків, що учні роблять зі своїх спостережень, такі детальні записи можна буде “згорнути”). Щоб урізноманітнити роботу, пропонуємо учням різнопланові завдання (на обчислення значень виразів, на доведення тотожностей, розв’язування рівнянь тощо).
Виконання письмових вправ
1. Замініть степінь на добуток, а потім цей добуток перетворіть у багаточлен стандартного вигляду:
1) (х + 10)2; 2) (1 – у)2; 3) (3а – 1)2; 4) (5 – 6b)2; 5) (а – 1)3.
2. Виконайте множення:
1) (u + v)(u – v);
2) (х2 + ху + у2)(х – у);
3) (z3 + z2t + zt2 + t3)(z – t);
4) (х + у)(х2 – ху + у2);
5) (х + у)(х3 – х2у + ху2 – у3);
6) (х + у)(х4 – х3у + х2у2 – ху3 + у4).
3. Спростіть вираз:
1) (х + 2)(х – 5) – 3х(1 – 2х);
2) (а + 0,3)(а – 0,2) + (а – 0,3)(а + 0,6);
3) а(а + 1)(а + 2) – 3(а – 2)(а + 2) + 2(а – 6);
4) а(а + 1)2 + (3а – 1)(4а + 1) – (2а – 1)(2а + 1).
4. Розв’яжіть рівняння:
1) (х + 3)(х – 2) – (х + 4)(х – 1) = 3х;
2) (2х + 6)(7 – 4х) = (2 – х)(8х + 1) – 3.
5. Спростіть вираз та обчисліть його значення: (2х – 3)(x – 1) + (x + 3)(3х + 1), якщо х = –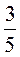 .
.
6. Доведіть, що для будь-якого значення змінної значення виразу (х + 1)(х2 – 2х + 5) + (х2 + 3)(1 – х) дорівнює 8.
7. Знайдіть чотири послідовних цілих числа, якщо добуток третього та четвертого на 2 більше від добутку першого та другого.
IV. Підсумки уроку
Виходячи з умінь, які виробили на уроці, прокоментуйте, які послідовні перетворення, за якими алгоритмами треба виконати під час спрощення виразу
(3а – 2b)(2a – 3b) – 6a(a – b).
V. Домашнє завдання
Повторити алгоритм перетворення добутку одночлена на багаточлен та двох багаточленів у багаточлен стандартного вигляду, виконати завдання.
Домашня самостійна робота
Варіант 1 | Варіант 2 |
№ 1. Виконайте дії: | |
1) -3х • (2х – 1); 2) (2а – b) • 8 b + 8b2; 3) 0,5а(2а – b) – 0,5b(2b – a); 4) (х – 2)(х + 3); 5) (2х2 – у2)(3у2 – х2); 6) 4у3 – (1 + 2у)(2у2 – у) | 1) (4y – 2)(2у); 2) 5а(а – 2b) + 10аb; 3) 14х(у – 0,2х) – 10у(х – 0,2у); 4) (х – 1)(х + 7); 5) (а2 – 4b2)(b2 – 4а2); 6) у3 – (3у + у2)(у – 3) |
№ 2. Розв’яжіть рівняння: | |
1) 2) (1 – х)(2 – х) = (х + 3)(х – 4) | 1) 2) (2 – х)(3 – х) = (х + 2)(х – 5) |
№ 3*. Навколо дачного будинку, а якого на 2 м більша за ширину, довжин заасфальтували доріжку довжиною 1 м. Площа доріжки 16 м2. Знайдіть довжину й ширину (розміри) будинку |
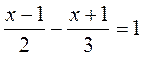 ;
;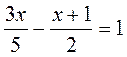 ;
;