Головна ⇒ 📌Математика ⇒ МНОЖЕННЯ МНОГОЧЛЕНІВ

МНОЖЕННЯ МНОГОЧЛЕНІВ

РОЗДІЛ 3 МНОГОЧЛЕНИ

&10. МНОЖЕННЯ МНОГОЧЛЕНІВ

Ви знаєте, як додавати й віднімати многочлени. Розглянемо властивості дій другого ступеня з многочленами.

1. Множення одночлена на многочлен

Запам’ятайте!

Помножити одночлен на многочлен – означає скласти вираз, що є сумою добутків даного одночлена і кожного члена многочлена, та спростити його, якщо це можливо.

Задача 1. Знайдіть добуток одночлена у2 і многочлена – х + 7х2у – 2у – 5.

Розв’язання. Складемо вираз, що є добутком одночлена і многочлена та помножимо

одночлен на кожний член многочлена:

У2 ∙ (-х + 7х2у – 2у – 5) =

У2 ∙ (-х) + у2 ∙ 7х2у – у2 – 2у – у2 – 5.

Подамо отриманий вираз як многочлен стандартного вигляду:

7х2у2 – ху2 – 2у3 – 5у2.

Зверніть увагу:

Щоб не помилитися, виконуючи множення одночлена на многочлен:

1) візьміть многочлен у дужки;

2) порахуйте кількість доданків у дужках;

3) щоразу називайте кількість доданків у дужках і номер того доданка, який множите на одночлен перед дужками, наприклад:

“У дужках чотири доданки, множимо перший доданок. У дужках чотири доданки, множимо другий доданок і т. д.”.

? Чи зміниться

добуток одночлена і многочлена, якщо їх поміняти місцями? Ні. Наприклад, у ∙ (х + 1) = ху + у, (х + 1) ∙ у = ху + у. Звідси у(х+ 1) = (х + 1)y.

Загалом, множення одночлена і многочлена підкоряється переставному і сполучному” законам множення, а також розподільному закону множення відносно додавання.

2. Множення многочленів

Запам’ятайте!

Помножити многочлен на многочлен – означає скласти вираз, що є сумою добутків кожного члена одного многочлена на кожен член іншого многочлена, та спростити його, якщо це можливо.

Задача 2. Знайдіть добуток многочленів у2 – у і 2у – х – 1.

Розв’язання. Складемо вираз, що є добутком даних многочленів. Шуканий вираз є сумою добутків кожного члена першого многочлена на другий многочлен:

(у2 – у) ∙ (2у – х – 1) =

= у2 – (2у – х – 1 + (-у)(2у – х – 1).

Далі скористаємося правилом множення одночлена на многочлен:

У2 – (2у – х – 1) + (-у) ∙ (2у – х – 1) = 2у3 – ху2 – у2 – 2у2 + ху + у.

Подамо отриманий многочлен у стандартному вигляді. Для цього зведемо подібні доданки:

-2у3 – ху2 – y2 – 2у2 + ху + у =

-2у3 – ху – 3у + ху + у.

Зверніть увагу:

Щоб помножити два многочлени:

– помножте кожний член одного многочлена на кожний член іншого многочлена і запишіть суму цих добутків;

– подайте кожний член отриманого многочлена у стандартному вигляді;

– зведіть подібні доданки, якщо вони є.

При множенні двочлена на двочлен можна скористатися формулою:

(а + b)(с + d) = ac + ad + bc + bd.

? Чи можна підносити многочлени до степеня? Так. Наприклад:

(а + b)2 = (a + b)(a + b),

(а + b)3 = (а + b)(а + b)(a + b).

Узагалі, степенем многочлена з натуральним показником n, більшим за 1, називається добуток п множників, кожний з яких є даним многочленом.

Множення многочленів підкоряється переставному і сполучному законам множення, а також розподільному закону множення відносно додавання. Якщо позначити многочлени літерами А, В і С, то коротко можна записати так:

AВ = ВA, (АВ)С = A(ВС), (A + В)С = АС + ВС для будь-яких А, В і С.

Дізнайтеся більше

У вас могло виникнути запитання: чи можна ділити многочлен на многочлен? Так. Ділити один многочлен на інший можемо за умови, що степінь многочлена-діленого не є меншим за степінь многочлена-дільника. За аналогією з числами, ділення многочлена на многочлен можна виконувати “кутом”. Наприклад, треба поділити многочлен 2х3 + 3×2 – х – 4 на двочлен х – 1. Запишемо ділене і дільник так само, як і при діленні чисел. Члени многочлена – частки добираємо так само, як і цифри числа-частки.

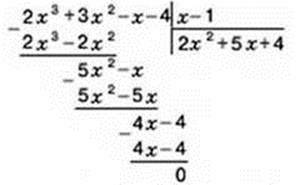
Отже, (2х3 + 3х2 – х – 4) : (х – 1) = 2х2 + 5х + 4.

Зауважимо, що як і при діленні чисел, не будь-які многочлени можна поділити націло один на одний. Більш грунтовно ділення многочленів ви зможете вивчати в поглибленому курсі алгебри.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Як помножити одночлен на многочлен?

2. Як помножити многочлен на многочлен?

3. Що називається степенем многочлена з натуральним показником, більшим за 1?

4. Які закони справджуються для множення многочленів?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

472. Чи правильно виконано множення одночлена і многочлена:

1)х ∙ (х + 1) = 2х + 1;

2)х ∙ (х + 1) = х2 + 1;

3)х ∙ (х + 1) = х2 + х?

473. Чи правильно виконано множення многочленів:

1) (1 + х) ∙ (х + 2) = 2 + 2х; 3) (1 + х) ∙ (х + 2) = х2 + 2х + 2;

2) (1 + х) ∙ (х + 2) = 3 + 2х; 4)(1 + х) ∙ (х + 2) = x2 + 3х + 2?

474. Яка з рівностей є правильною:

1 )(х + у)2=(х + у) ∙ 2;

2) (1 + х)2 = (1 + х) ∙ (1 + х);

3) (у + х)3 = (у + х) ∙ (у + х) ∙ (у + х)?

475. Знайдіть добуток одночлена і двочлена:

1) – х і х + у;

2) х і х – у;

3) х і х – 1;

4) – х і х -1;

5) m і m + 2;

6) m – 2 i – m;

7) х і 1 – х;

8) х і 1 +х;

9) а + b і -1;

10)а2 + b2 і 4;

11)mn – n і 7;

12)m2 + 6 і 5.

476. Знайдіть добуток:

1) (n – m) ∙ 2nm;

2) 10 < (-5d – 0,4);

3) k2 ∙ (k2 + k + 3);

4) 0,2х ∙ (0,25х +1,5х2 + х);

5) 5d – (d2 + d + 1);

6) (-p + 3) (-0,2p2);

7) 8х(-х2 + 2х – 1);

8) X ∙ (-Y – x + xy – 3).

477. Знайдіть добуток:

1) m(m + m2); 3)-2х(х2 + 9);

2) m – (m – m); 4) аb ∙ (a2 + b2 – ab + 0,5).

478. Перетворіть вираз у многочлен стандартного вигляду:

1) 3а ∙ (а – а2 );

2) (а2 + b + с) ∙ 3b;

3) (-5а + b) – (-2а2);

4) 2 ∙ (3а2 + 2а+ 4);

5) (х + 3у) (-10х2);

6) (х2 – 4х) ∙ (-2ху);

7) (0,1 m + 0,3n2) ∙ 10mn;

8) a(b – c + cb).

479. Спростіть вираз:

1) 3х ∙ (7у – х) ∙ 2; 3) (2k2 + 5k – 3) ∙ (-3k);

2) у ∙ у ∙ (х – 2у2); 4) b ∙ (a2 + b2) ∙ ab.

480. Розв’яжіть рівняння:

1) 2(4 – х) + 3(2х – 8) = 0; 3) х(х – 4) – (х2 + 8) = 0;

2) 5(2 + 4х) – 8(-х – 1) = 0; 4) (10х + 7)4х – 5х(8х – 1) + 33 = 0.

481. Розв’яжіть рівняння:

1)2(4х – 1) + 4(х – 2) – 14 = 0; 3) х(х – 8) + 5х(х – 1) – 6х2 = 26;

2) 4(2 – х) + 5(8х – 1) = 0; 4) -4х2(9 + х) + 3х( 12х – 1 ) = 2(-2×3 – 9).

482. Знайдіть добуток двочленів:

1) у + х і – х – у;

2) у + х і х + у,

3) y + x і – х + у;

4) – у + х i х – у;

5) 2а + х і 2х + а;

6) 3а + b і 3а – b;

7) 2х + х і х -4;

8) у2 + 5 і х2 + 2.

483. Знайдіть добуток двочленів:

1) 8 + х і 4х – 5;

2) х + 4 і – х – 6;

3) 2 + х і 2х + 1;

4) х + 3 і х + 9;

5) 2х + 1 і – х – 4;

6) у – 5 і х – 4;

7) 2y + х і 2х+ у;

8) х2 + 4 і – х2 – 6;

9) х2 – 2 і – х2 + 5.

484. Розв’яжіть рівняння:

1) (5 – х)(х + 6) + х(х – 8) = 0;

2) (х – 1)(х + 1) – (х – 3)(х – 2) = 0;

3) (10 – х)(9х – 3) + (1 + 3х)(3х – 1) = 154;

4) (х – 3)(х – 4) = (х – 8)(х + 1).

485. Розв’яжіть рівняння:

1) (1 – х)(х + 1) + х(х – 6) = 0;

2) 2х(х + 5) – (2х – 8)(х + 10) = 0;

3) (2х + 6)(5х – 3) – (1 + 10х)(х + 12) = -30(х + 1);

4) (х – 1)(х – 6) = (х – 2)(х – 5).

486. Знайдіть квадрат двочлена:

1) n + m; 2) х + 3; 3) а + 2с; 4)2а – с; 5)-х – 2.

487. Знайдіть квадрат двочлена:

1)х + 1; 2) х – 1; 3) n – 3m; 4)-у + 4.

488. Перетворіть вираз у многочлен стандартного вигляду:

1) a2(a2 + 1) – а4(a4+ 1) + а8(а8 + 1) – a16(a16 + 1);

2) a(b – c) + b(c – а) + с(a – b);

3) ((х3 + 1) х + 1) х + 1;

4) хуz(х2у2 – z2) + х3(-zy3 + z2) – z3 (-ху + 2).

Який степінь утвореного многочлена?

489. Спростіть вираз:

1)(х2(х + y2 + хy) – (1 + у)х3)у3 – х2 у5;

2) 0,3abc(2ab + с) + (-b2a2 – 0,7асb)0,6с;

3) 0,75x11y5(x2 + 1Y7x) – x3y3((xy)9 – X10y2) + 1;

4) 16b2a14( а2b3 – 0,25аb) – 3а13(b5а3 – b3).

490. Доберіть одночлени, якими можна доповнити порожні клітинки таблиці 10.

Таблиця 10

Многочлен	Х + 2y	3а + b + 2а3	3а + 4b	2с2 + 1 – с
Одночлен
Добуток	5х3 + 10 х2у	6аb + 2b2 + 4bа3	6а2+ 8аb	2dc3 + dc – c2d

491. Розв’яжіть рівняння:

1) (х + 1) (х + 5) + (0,5х – 1 )6х = 4(1 + х2);

2) (х – 1 )(2х – 1 )х + (1 – 2х2)(х – 1) = 2х -1;

3) (х + 6)2 – (х – 2)2 = 0;

4) (х + 1)2 + (х – 1)2 = 2.

492. Доведіть, що значення виразу не залежить відзначення х:

1) (1 + х)(х + 9) – (4 + х)(х + 6);

2) (4 + х)(х – 7) – х(х – 3);

3) (2x – 1)(3x + 2) – (2 + 6x)(x – );

4) (-1 + 0,24 х)(х – 5) + (3 – 0,8х)(0,3х – 1,625).

493. Доведіть, що вираз набуває додатних значень за будь-якого значення т:

1) 2m(m3 + 3m – 2) – (-4m – 1);

2) (2 + m)2 – 4(m – 2) + m2;

3) (4 + 5m)(3m – 1) – 7(m – 4) + 72.

494. Спростіть вираз і знайдіть його значення:

1) (х + 4)(х + 3) – (х + 4)(х + 4) – 2х + 4, якщо х = -0,02;

2) 3(х – 2)2 + 0,5х(2х + 4) – (1 – 2х)2 – 3, якщо х = -1,01.

495. Спростіть вираз:

1) (х – у)(х2 + ху + у2) – (х + у)(х2 – ху + у2);

2) (2b – а)(4b2 + a2 + 4аb);

3) (0,2x + y)(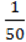X2 – Xy + y2);

4) (х2 + 4х + 2х3 + 3)(х + 2) – 2(х3 + 1 )(х + 2);

5) (-2х + 4у)(-х + y) + 4у(у – х);

6) b(-а + b)(5 – ab) – b2 (ba + 2 + а2).

496. Перетворіть вираз у многочлен стандартного вигляду:

1) (с3 + 10)с – (с2 + 10)(с2 + 50) + 60(с + 1 )2 – 10( 10с – 5);

2) (x + )(x – 1)(x + 1) – x3 + X2 + ;

3) (х – 0,8)(5 – х) + х2(х – 4) – (2 – х)3 – 3х2 + 0,2х;

4) (-а2 +3b2)(-3b2 – а2) – (а + 4)2 + (2b + 8)(1,5b3 + 2);

5) (-3X3y + 1Y2)(x3 – 5y) + (9y2 – x3)(-0,2×3 + y) – x3y(17,5y – 1);

6) (Xy – 0,3×2)(zy – X) – (1,6x + 0,8xz)(y2 – Xy) – 0,1×2(1,5x + 2y).

497. Перетворіть вираз у многочлен стандартного вигляду:

1)(b2- 2b)b + 2b (b – 1) – b(b + 1)2;

2) (0,3a3 – 2,1a2 – 4)(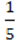A2 – a – 7) + a4(0,3 – 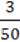A);

3) (2abc – 4b2с + 5аc)(6с + 3а2) + 6abc(2ba – 2с – а2) – 3 ас(10с + 5а2);

4) (а + b + с) (а + b – c) – (b + a)2.

498. Перетворіть вираз у многочлен стандартного вигляду:

1) (а + b + с)2;

2) (х + y + 1)2;

3) (а – b – с)2;

4) (2х + 3у + 5)2

499. Спростіть вираз:

1) хn+1(х2n-1 + 1) – (хn+1)2 + хn(-х2n + х);

2) хn(хn – хm) + хm(хn – хm) – х2m(х2n + 1) – х2n (х2m + 1);

3) аn+2 – a(bn+1 + an+1) – b2n(a2b ∙ b2a – (ab)3;

4) аn+1bn(b3 + a2) + а3b(-anbn-1 – bn+2an-2 + 1).

500. Знайдіть добуток (х – 1)(х – 2) … (х – 100), якщо:

1)х = 34; 2) х = 87.

501. Доведіть тотожність:

1) (а – 1 )(а5 + а4 + а3 + а2 + а +1) = а6 – 1;

2) (а + 1)(а4 – а3 + а2 – а + 1) = а5 + 1;

3) (a + b)2 – (c + d)2 + (a + c)2 – (d + b)2 = 2(a – d)(a + b + c + d);

4) 2(а + b + с)2 – (с + b)2 – (a + с)2 – (a + b)2= 2(ab + bс + ас).

502. Спростіть вираз:

1) (2х – 3y)(2х + 3y)2 – (2х + 3у)(2х – 3y)2;

2) (х – у) +(х + у) ;

3) (m – 1)3 + (m + 1)3;

4) (а2 + ab + b2) (а2 – ab + b2) (а4 – а2b2 + b4).

503. Доберіть цілі значення а, b і с, за яких для довільного х є правильною рівність:

Ах2(х + 1) + b(х2 + 1 )(х – 6) + сх(х2 + 1) = 5х + х2 + 6

504. Добуток двоцифрового числа і суми його цифр на 20 більший, ніж сума квадратів його цифр. Знайдіть це число.

505. Помноживши двоцифрове число на суму його цифр, отримали 814. Знайдіть це число.

506. Якщо між цифрами двоцифрового числа вписати це саме число, то отримане число буде більшим за дане в 77 разів Знайдіть це число.

507. Знайдіть шестицифрове число, яке зменшується в три рази при перенесенні останньої цифри, що дорівнює 1, на перше місце.

508. Знайдіть усі числа 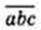, якщо 0,1 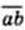∙ с =с + a + b.

509. Доведіть, що число 1 + 123457 ∙ 123455 є квадратом цілого числа.

510. Доведіть, що число 20142014 + 20142013 ∙ 20142014 ∙ 20142015 є кубом цілого числа.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

511. Площа прямокутника – 100 м2. Якщо кожну його сторону збільшити на 5 м, то площа прямокутника збільшиться на 170 м2. Знайдіть периметр початкового прямокутника.

512. Стіл в х разів дешевший від шафи, а стілець – в х разів дешевший від стола. Скільки заплатили за 16 стільців, 3 столи і 2 шафи, якщо стілець коштує а грн?

ЗАДАЧІ НА ПОВТОРЕННЯ

513. одного населеного пункту в протилежних напрямках виїхали два велосипедисти. Перший їхав зі швидкістю 8 км/год, а другий – зі швидкістю, більшою на 4 км/год. На якій відстані один від одного будуть знаходитися велосипедисти через 2 год після виїзду?

514. Із двох населених пунктів, відстань між якими 40 км, одночасно назустріч один одному виїхали два велосипедисти. Перший їхав зі швидкістю 10 км/год, а другий – зі швидкістю, більшою на 5 км/год. На якій відстані один від одного будуть знаходитися велосипедисти через 2 год після виїзду?