Головна ⇒ 📌Довідник з математики ⇒ Найпростіші перетворення радикалів
Найпростіші перетворення радикалів
Математика – Алгебра
Степенева функція
Найпростіші перетворення радикалів
1. Винесення множника за знак радикала
Приклади
1) Винесіть множник за знак кореня (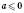 , b>0):
, b>0):
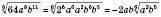 .
.
2) Винесіть множник за знак кореня (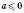 ,
, 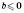 ):
):
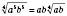 .
.
Зверніть увагу: 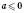 ,
, 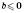 , але
, але 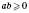 ,
, 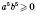 .
.
3) Винесіть множник за знак
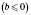 :
: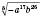 .
.Даний вираз має зміст при
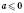 , а звідси
, а звідси 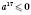 ,
, 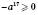 .
.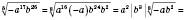
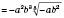 . (Скористались тим, що
. (Скористались тим, що 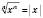 , тому
, тому 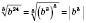 .)
.)2. Внесення додатних множників під знак радикала
Приклади
1)
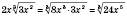 .
.2)
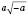 . Цей вираз має зміст при
. Цей вираз має зміст при 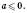
Отже,
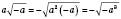 .
.3)
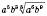 . Цей вираз має
. Цей вираз має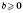 .
.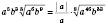 .
.3. Зведення до раціонального вигляду членів дробових ірраціональних виразів
Приклади
1) Знаменник – одночленний ірраціональний вираз.
а)
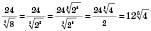 ;
;б)
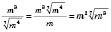 ,
, 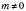 .
.2) Знаменник – двочлен відносно квадратних коренів. Використовують тотожність
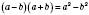 .
.а)
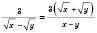 , ОДЗ – область допустимих значень (тобто множина значень х, для яких усі вирази, що входять до рівняння, мають зміст):
, ОДЗ – область допустимих значень (тобто множина значень х, для яких усі вирази, що входять до рівняння, мають зміст): 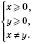
б)
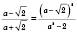 ,
, ОДЗ:
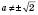 .
.3) Використання тотожностей:
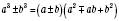 .
.а)
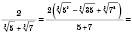
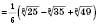 .
.б)
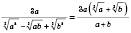 ,
, 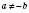 .
.4. Добування кореня з радикалів
Приклад
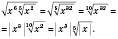
Related posts:
- Перетворення коренів УРОК 34 Тема. Перетворення коренів Мета уроку. Познайомити учнів з найпростішими перетвореннями радикалів: винесення множника за знак радикала; внесення множника під знак радикала; зведення радикалів до найпростішого (нормального) вигляду; ознайомлення з поняттям подібних радикалів. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 1-12, 17-24 із “Запитання і завдання для повторення до розділу III. 2. […]...
- Порівняння радикалів УРОК 35 Тема. Порівняння радикалів Мета уроку. Формування умінь учнів порівнювати радикали. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 25-37 із “Запитання і завдання для повторення” до розділу III. 2. Самостійна робота. Варіант 1 1. Знайдіть область визначення виразу: а) ; б) . (3 бали) 2. Обчисліть: а) ; б) 5; в) –. […]...
- ПЕРЕТВОРЕННЯ ВИРАЗІВ РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ &3. ПЕРЕТВОРЕННЯ ВИРАЗІВ Ви вже знаєте, що два числові вирази МОЖУТЬ мати рівні значення, і тоді ці вирази можна прирівняти. Наприклад, 10 ∙ 2 + 5 = 31 – 2 ∙ 3. Про вирази зі змінними такого однозначно сказати не можна. Розглянемо приклади. Задача 1. Чи можна прирівняти вирази: 1) […]...
- Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
- Дії над радикалами УРОК 36 Тема. Дії над радикалами Мета урокую Познайомити учнів з діями над радикалами: додавання і віднімання, множення і ділення; піднесення радикала до степеня; добування коренів з радикалів; зведення до раціонального вигляду членів дробових ірраціональних виразів. І. Перевірка домашнього завдання 1. Три учні відтворюються розв’язування вправ № 22, 26 і 38 на дошці. 2. У […]...
- Тотожні перетворення виразів, що містять квадратний корінь Урок № 43 Тема. Тотожні перетворення виразів, що містять квадратний корінь Мета: поглибити знання учнів відомостями про способи перетворення дробових виразів, що містять квадратні корені; сформувати вміння застосовувати вивчені способи дій для перетворення дробових виразів, що містять квадратні корені, у завданнях, передбачених програмою з математики. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: […]...
- Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...
- Підсумковий урок з теми “Арифметичний квадратний корінь з числа та його властивості. Перетворення ірраціональних виразів” Урок № 45 Тема. Підсумковий урок з теми “Арифметичний квадратний корінь з числа та його властивості. Перетворення ірраціональних виразів” Мета: повторити, узагальнити та систематизувати знання та вміння учнів щодо означення, властивостей арифметичного квадратного кореня з числа та способів його застосування для перетворення числових та буквених виразів. Тип уроку: систематизація та узагальнення знань і вмінь. Наочність […]...
- РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ СПОСОБОМ ВИНЕСЕННЯ СПІЛЬНОГО МНОЖНИКА ЗА ДУЖКИ Цілі: – навчальна: удосконалити вміння учнів виконувати розкладання многочленів на множники способом винесення спільного множника за дужки; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати впевненість у власних силах, спостережливість; формувати вміння самоорганізовуватися; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід […]...
- Винесення множника з-під знака кореня, внесення множника під знак кореня Урок № 41 Тема. Винесення множника з-під знака кореня, внесення множника під знак кореня Мета: домогтися засвоєння учнями змісту алгоритму перетворення, що має назву винесення множника з-під знака кореня та змісту алгоритму перетворення, що має назву внесення множника під знак кореня; сформувати вміння учнів виконувати названі перетворення за вивченими алгоритмами, а також застосовувати ці перетворення […]...
- Розподільна властивість множення. Зведення подібних доданків Урок № 88 Тема. Розподільна властивість множення. Зведення подібних доданків Мета: завершити роботу з відпрацювання навичок використання розподільної властивості множення для: а) обчислень; б) розкриття дужок; в) зведення подібних доданків; г) винесення найбільшого спільного множника за дужки. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання Усні вправи 1. Обчисліть, використовуючи […]...
- Перетворення виразів Уроки № 122, 123 Тема. Перетворення виразів 1. Спростіть вираз і знайдіть його значення при даних значеннях букв: а) -12b – 7b + 10b – b при b = -0,1; 2; -1; -5,7; 0; Б) -5а – 8а – 2а – 15a при а = -0,6; ; ; 0,002; -1; В) -4c + 9с – […]...
- ТОТОЖНІСТЬ. ТОТОЖНІ ПЕРЕТВОРЕННЯ ВИРАЗУ Цілі: – навчальна: сформувати поняття тотожності, тотожних перетворень виразів; формувати вміння розв’язувати задачі, які передбачають застосування цих понять; формувати вміння виконувати тотожні перетворення виразів; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати вміння виділяти головне в досліджуваному матеріалі; – виховна: виховувати зацікавленість у пізнанні нового, творче ставлення до справи, старанність; Тип уроку : засвоєння […]...
- Перетворення раціональних виразів – Раціональні вирази Математика – Алгебра Раціональні вирази Перетворення раціональних виразів Будь-який раціональний вираз можна подати у вигляді дробу або цілого виразу. Це можна зробити на основі правил дій над дробами та цілими виразами. Треба розуміти, що для раціональних виразів мають місце відомі властивості дій (переставна та сполучна властивість додавання і множення та ін.). Запис можна вести у […]...
- Розкладання многочленів на множники способом винесення спільного множника за дужки Розділ 1. ЦІЛІ ВИРАЗИ & 10. Розкладання многочленів на множники способом Винесення спільного множника за дужки У 6 класі ми розкладали складені числа на прості множники, тобто подавали натуральні числа у вигляді добутку. Наприклад, 12 = 22 ∙ 3; 105 = 3 ∙5 ∙ 7 тощо. Подати у вигляді добутку можна і деякі многочлени. Це […]...
- Тотожні вирази. Тотожність. Тотожні перетворення Урок № 15 Тема. Тотожні вирази. Тотожність. Тотожні перетворення Виразів Мета: систематизувати й узагальнити знання учнів про перетворення виразів, набуті учнями в 5-6 класах; поглибити знання про види виразів (тотожні вирази); оволодіти новою термінологією. Тип уроку: засвоєння знань. Хід уроку І. Перевірка домашнього завдання № 2 – зібравши зошити, перевіряємо якість виконання завдань. Розв’язання і […]...
- Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Розділ 1. ЦІЛІ ВИРАЗИ & 2. Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Знайдемо значення виразів 2(х – 1) і 2х – 2 для деяких даних значень змінної х. Результати запишемо в таблицю: Х -4 -3 -2 -1 0 1 2 3 4 2(х – 1) -10 -8 -6 -4 -2 0 2 4 […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...
- Перетворення цілих виразів Цікаві вправи Тема. Перетворення цілих виразів 1. Ігрові моменти. А) За 1 хвилину записати якомога більше таких двочленів, щоб у разі винесення спільного множника за дужки в дужках залишилось 2х – 3; Б) За 1 хвилину записати якомога більше таких дробів із знаменником х(х – 2), які можна скоротити. В) За 1 хвилину придумайте якомога […]...
- Множення Математика – Алгебра Раціональні числа Множення Щоб знайти добуток двох чисел із різними знаками, треба перемножити їхні модулі й поставити перед одержаним числом знак “–”. Щоб перемножити два від’ємних числа, треба перемножити їхні модулі (тобто добуток двох від’ємних чисел є додатне число). При зміні знака одного з множників змінюється знак усього добутку. Якщо добуток містить […]...
- Розкладання многочленів на множники Математика – Алгебра Многочлен Розкладання многочленів на множники Розкласти многочлен на множники означає подати його як добуток кількох многочленів. Винесення спільного множника за дужки Спосіб розкладання многочлена на множники на основі розподільної властивості множення називається винесенням спільного множника за дужки. Приклад . НСД . Це означає, що за дужки можна винести числовий множник 2. В […]...
- ВИРАЗИ ТА ЇХ СПРОЩЕННЯ Розділ 5 ВИРАЗИ І РІВНЯННЯ У розділі дізнаєтесь: Ü про вирази та їх спрощення; Ü які є властивості рівностей; Ü як розв’язувати рівняння на основі властивостей рівностей; Ü які види задач розв’язують за допомогою рівнянь; що таке перпендикулярні прямі та як їх будувати; Ü які прямі називаються паралельними та як їх будувати; Ü що таке […]...
- Тотожні перетворення раціональних виразів Урок № 19 Тема. Тотожні перетворення раціональних виразів Мета: закріпити знання учнів про алгоритми тотожних перетворень раціональних виразів, способи перетворення відношення двох дробових виразів та про схеми застосування властивостей арифметичних дій під час перетворення раціональних виразів. Тип уроку: корекція знань, відпрацювання навичок. Наочність та обладнання: опорний конспект “Тотожні перетворення алгебраїчних виразів”. Хід уроку I. Організаційний […]...
- РОЗПОДІЛЬНИЙ ЗАКОН РОЗДІЛ 3 ДІЇ ДРУГОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 12. РОЗПОДІЛЬНИЙ ЗАКОН Вирази, що містять дії додавання та множення, можна групувати по-різному. Розглянемо приклад. Задача 1. У кожному відділенні свого ранця Андрій знайшов по 10-копійковій і 5-копійковій монетці. Яку суму грошей знайшов Андрій, якщо у ранці 3 відділення? Розв’язання. Розв’язати задачу можна двома способами. Для […]...
- Повторення та систематизація матеріалу, вивченого в 7 класі. Перетворення виразів Урок № 83 Тема. Повторення та систематизація матеріалу, вивченого в 7 класі. Перетворення виразів Мета: повторити та систематизувати знання про види та способи перетворення буквених виразів, вивчених у 7 класі; повторити та вдосконалити вміння використовувати набуті знання під час розв’язування типових вправ. Тип уроку: повторення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент […]...
- ПОВТОРЕННЯ. ПЕРЕТВОРЕННЯ ВИРАЗІВ Цілі: – навчальна: узагальнити та систематизувати знання учнів про види та способи перетворення виразів; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять;_ – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. Обладнання та наочність: […]...
- Перетворення виразів. Повторення та систематизація матеріалу 5-6 класів Урок № 1 Тема. Перетворення виразів. Повторення та систематизація матеріалу 5-6 класів Мета: систематизувати та узагальнити знання учнів про перетворення виразів, набуті у 5-6 класах. Тип уроку: повторення та систематизація знань. Хід уроку I. Організаційний момент Вступна бесіда. II. Актуалізація опорних знань На цю тему відводиться два уроки. @ Тотожні перетворення виразів є одним з […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ПЕРЕТВОРЕННЯ ВИРАЗІВ Цілі: – навчальна: удосконалити вміння застосовувати перетворення виразів до розв’язування задач; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати культуру усного та писемного мовлення; – виховна: виховувати старанність, дисциплінованість, працьовитість; Тип уроку : удосконалення і застосування знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...
- Тотожні вирази. Тотожні перетворення виразів Урок № 16 Тема. Тотожні вирази. Тотожні перетворення виразів Тотожності Мета: закріпити знання учнів про основні поняття, вивчені на попередньому уроці; відпрацювати навички. володіння термінологією; вдосконалити вміння складати вирази за умовою, виконувати тотожні перетворення виразів, обчислювальні навички. Тип уроку: застосування знань, засвоєння навичок. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань @ Ступінь розуміння […]...