Нерівність трикутника
Урок № 38
Тема. Нерівність трикутника
Мета: домогтися засвоєння змісту теореми, що виражає нерівність трикутника та схему її доведення та наслідку з теореми; виробляти вміння відтворювати формулювання доведених на уроці тверджень та застосувати для розв’язування задач.
Тип уроку: засвоєння знань, умінь та навичок.
Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Нерівність трикутників та наслідки з неї”.
ХІД УРОКУ
I. Організаційний момент
II. Перевірка домашнього завдання
Організувати
III. Мотивація навчальної діяльності. Формулювання мети уроку
Перевіривши виконання домашнього завдання, учні активізують свої знання щодо співвідношення між сторонами й кутами трикутника. Для мотивації вивчення нерівності трикутника вчитель може запропонувати задачу.
Задача. Використавши циркуль та лінійку, побудуйте трикутник зі сторонами:
А) 3 см, 4 см, 5 см;
Б) 3 см, 4 см, 1 см;
В) 3 см, 4 см, 8 см.
Порівняйте умови задач та виконані побудови. Що ви помітили?
Якщо учні володіють алгоритмом побудови трикутника за трьома сторонами, то вони
Пошук цього зв’язку – і є основною дидактичною метою уроку.
VI. Актуалізація опорних знань
З метою успішного сприйняття доведення теореми про нерівність трикутника слід активізувати знання учнів про співвідношення між сторонами й кутами трикутника, властивість кутів рівнобедреного трикутника, аксіому вимірювання відрізків та кутів. Це можна провести або у формі роботи за готовими рисунками, або у формі фронтальної бесіди.
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Нерівність трикутника та її доведення.
2°. Наслідок з нерівності трикутника.
3°. Застосування нерівності трикутника під час розв’язування задач.
Методичний коментар
Формулюючи теорему про нерівність трикутника, слід пояснити значення слова “кожна” в математиці. На засвоєння формулювання теореми запропонувати учням таке завдання: записати нерівність трикутника для сторін трикутника MNK.
Доведення теореми про нерівність трикутника здійснюється із посиланнями на означення і властивість рівнобедреного трикутника, аксіому вимірювання кутів та доведену на попередньому уроці теорему про співвідношення між сторонами й кутами трикутника.
Після доведення нерівності трикутника формулюється як наслідок твердження про взаємне розташування трьох точок у разі виконання рівності між одним із відрізків та сумою двох інших.
Якщо дозволяє підготовка учнів, можна сформулювати й довести ще один опорний факт: будь-яка сторона трикутника більша за різницю двох інших сторін.
Як приклади задач на застосування нерівності трикутника можна розглянути такі задачі:
А) чи існує трикутник із заданими довжинами сторін;
Б) на знаходження найкоротшого шляху на площині;
В) на визначення довжини третьої сторони трикутника за відомими довжинами двох інших.
Працюючи над засвоєнням нового матеріалу, бажано звертатися до таблиці “Нерівність трикутника”.
Таблиця

VI. Первинне усвідомлення нових знань
Виконання письмових вправ
Рівень А
1. Знайдіть сторону рівнобедреного трикутника, якщо дві інші його сторони дорівнюють:
А) 14 см і 6 см; б) 5 см і 10 см; в) 3 см і 4 см.
2. Доведіть, що точки A, B і C лежать на одній прямій, якщо AB =12,3 см, BC = 9,7 см, AC = 2,6 см.
Рівень Б
1. Сторона рівнобедреного трикутника на 3 см більша за іншу сторону. Знайдіть усі сторони трикутника, якщо його периметр дорівнює 18 см.
2. Дві сторони трикутника дорівнюють 1,2 м і 0,4 м. Знайдіть довжину третьої сторони, якщо вона вимірюється цілим числом метрів.
3. Доведіть, що медіана трикутника менша, ніж половина його периметра.
VII. Підсумки уроку
На рисунку 1 знайдіть і виправте помилку. (Поясніть двома способами)
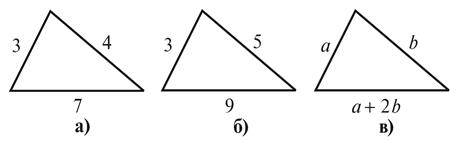
VIII. Домашнє завдання
Вивчити теоретичний матеріал. Письмово розв’язати задачі.
1. Знайдіть периметр рівнобедреного трикутника, дві сторони якого дорівнюють 2 см і 7 см.
2. Визначте, чи лежать точки A, B і C на одній прямій, якщо:
А) AB = 7,5 см, BC = 8,3 см, AC =11,5 см;
Б) AB =16,3 см, BC = 0,8 см, AC =15,5 см.
3. Периметр рівнобедреного трикутника дорівнює 70 м. Знайдіть сторони трикутника, якщо одна з них дорівнює 10 м.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.