Головна ⇒ 📌Математика ⇒ НЕРІВНОСТІ ТРИКУТНИКА

НЕРІВНОСТІ ТРИКУТНИКА

РОЗДІЛ 3 ТРИКУТНИКИ

& 15. НЕРІВНОСТІ ТРИКУТНИКА

Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему.

Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона.

Доведення. 1) Нехай у трикутнику ABC сторона АВ більша за АС. Покажемо, що кут С більший за кут В (мал. 189). Відкладемо на стороні АВ відрізок АКТ, що дорівнює АС.

Оскільки відкладений відрізок коротший від АВ, то точка

К лежить між точками А і В, а ∠ACK є частиною кута АСВ. Кути AKC і АС К рівні, тобто ∠1 = ∠2, бо ∆КАС – рівнобедрений. ∠1 більший за ∠B, бо є зовнішнім для трикутника ВKС. Тоді, весь кут С більший за ∠2, a ∠2 більший за ∠B. Цим доведено, що якщо в трикутнику АВ > АС, то ∠C > ∠B.

2) Hехай у трикутнику ABC кут С більший за кут В.

Доведемо, що тоді АВ > АС.

Сторони АВ і АС не можуть дорівнювати одна одній, бо інакше даний трикутник був би рівнобедреним і один з його кутів при основі не міг би бути більшим від іншого.

Не може сторона АВ бути і меншою за сторону АС, бо тоді ∠C був би меншим за ∠B. А оскільки сторона

АВ не дорівнює стороні АС і не менша від АС, то вона більша за АС.

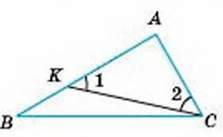
Мал. 189

Теорема 20 Кожна сторона трикутника менша від суми двох інших його сторін.

Доведення. Розглянемо довільний ДАОС і покажемо, що АВ < ВС + СА (мал. 190).

Для доведення відкладемо на продовженні сторони АС відрізок СР, що дорівнює стороні ВС, і розглянемо трикутник АВР. Кути СВР і СРВ – рівні, бо СВ = СР. Кут АВР – більший за ∠P.

А оскільки проти більшого кута лежить більша сторона, то АВ < АР. Врахувавши, що АР = АС + СР = АС + СВ, маємо:

АВ < АС + СВ.

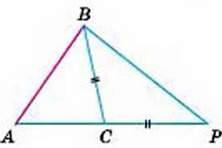
Мал. 190

Так само можна показати, що ВС < СА + АВ, АС < СВ + ВА.

З доведеної теореми випливає таке твердження.

Якщо точки А, В, С не лежать на одній прямій, то правильні нерівності: АВ < ВС + СА, ВС < СА + АВ, АС < СВ + ВА.

Кожну з цих трьох нерівностей називають нерівністю трикутники.

Для допитливих

Якщо точки А, В, С лежать на одній прямій, то одна з наведених вище нерівностей перетворюється в рівність, а дві інші залишаються правильними. Наприклад, якщо точка С лежить між точками А і В (мал. 191), то правильні такі співвідношення:

АВ – ВС + СА, ВС < СА + АВ, СА < АВ + ВС.

Враховуючи все сказане вище, можна зробити такий висновок.

Як би не були розташовані три точки А, В, С, то завжди: АВ < ВС + СА ВС ≤ СА + АВ, СА ≤ АВ + ВС.

Із трьох відстаней між будь-якими трьома точками кожна не перевищує суми двох інших.

Мал. 191

Запитання і завдання для самоконтролю

1. Сформулюйте і доведіть теорему про залежність між сторонами і кутами трикутника.

2. Сформулюйте і доведіть теорему про нерівності трикутника.

3. Сформулюйте нерівності трикутника XYZ.

4. Що означає вислів “точка В лежить між точками А і С”?

5. Як пов’язані між собою відстані між точками А, В і С, якщо точка В лежить між точками А і С?

6. Сформулюйте властивості відстаней між довільними точками А, В і С.

Виконаємо разом

1. Доведіть, що відрізок, який сполучає вершину рівнобедреного трикутника з довільною внутрішньою точкою основи, коротший за бічну сторону трикутника.

– Нехай АС – основа довільного рівнобедреного трикутника АВС, а К – довільна внутрішня точка його основи (мал. 192).

Покажемо, що ВК < АВ.

Кут АКВ – зовнішній у трикутнику КВС, тому ∠AKВ > ∠C. Оскільки ∠C = ∠A, то ∠AKВ > ∠A. Отже, у ∆АВК сторона ВК лежить проти меншого кута, ніж той, проти якого лежить сторона АВ. Тому ВК < АВ.

2. Пряма КР, що перетинає ∆АВС, паралельна стороні АС (мал. 193).

Яка зі сторін АВ чи ВС даного трикутника більша, якщо ВК < ВР?

– Пронумеруємо деякі кути, як показано на малюнку 193. Відповідні кути при паралельних прямих і січній рівні, тому ∠1 = ∠3 і ∠2 = ∠4. Оскільки в трикутнику ВКР ВК < ВР, то ∠4 < ∠3, тоді і ∠2 < ∠1.

Отже, АВ < ВС.

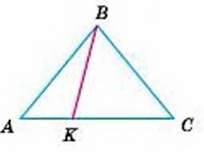
Мал. 192

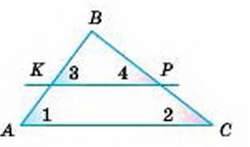
Мал. 193

ЗАДАЧІ І ВПРАВИ

Виконайте усно

442. Дивлячись на малюнок 194, порівняйте сторони АВ і ВС трикутника ABC, якщо:

1) ∠A < ∠C; 4) ∠A < ∠C;

2) ∠A > АС; 5) ∠A = 60°, ∠B = 70°;

3) ∠A = ∠C; 6) ∠B = 80°, ∠C = 40°.

Мал. 194

443. Доведіть, що коли кожну сторону рівнобедреного трикутника збільшити, наприклад, на 1 м, то утворений трикутник також буде рівнобедреним.

444. Чи можна кожний кут трикутника збільшити, наприклад, на 10°?

445. Яка зі сторін трикутника ABC найбільша, а яка – найменша, якщо:

1) ∠A = 45°, ∠B = 60°;

2) ∠A = 50°, ∠B = 100°;

3) ∠B = 75°, ∠C = 90°?

446. Який кут трикутника АВС – найбільший, а який – найменший, якщо:

1) АВ = 3 м, ВС = 4 м, АС = 5 м;

2) АВ – ВС = 2 м, ВС – АС = 1м?

447. Чи може основа рівнобедреного трикутника бути вдвічі довшою за бічну сторону? А вдвічі коротшою?

448. Чи може кожний кут трикутника бути меншим за 60°?

449. ЧИ існує трикутник, КОЖНИЙ кут якого більший за 60°?

450. Доведіть, що висота трикутника не довша за медіану, проведену з тієї самої вершини.

451. ЧИ може одна сторона трикутника дорівнювати половині його периметра?

452. Доведіть, що кожна сторона трикутника менша від його півпериметра.

453. Чи може сума двох сторін трикутника дорівнювати його півпериметру?

454. Доведіть, що кожна сторона трикутника довша за піврізницю інших його сторін.

455. Чи існує трикутник, одна сторона якого дорівнює різниці двох інших?

456. У трикутнику ABC сторони АВ і АС дорівнюють відповідно 5 см і 8 см. Якою завдовжки може бути сторона ВС?

457. Доведіть, що кожна сторона чотирикутника коротша від суми трьох інших його сторін.

458. Дві сторони трикутника дорівнюють 98 см і 28 см. Яким може бути периметр цього трикутника?

459. Сума двох рівних сторін трикутника становить 0,6 периметра. ЧИ правильно, що кут між рівними сторонами більший за 60°?

Практично завдання

460. Для оздоблення серветки квадратної форми досить 140 см мережива (мал. 195). Господиня вирішила розрізати серветку на два рівні трикутники і обшити дві трикутні серветки по периметру. Чи вистачить їй 210 см мережива?

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

461. Сума двох кутів, утворених при перетині двох прямих, дорівнює 200°. Знайдіть міри двох інших кутів.