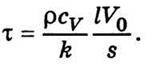Нестаціонарна теплопровідність
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 5 ЯВИЩА ПЕРЕНЕСЕННЯ
5.9. Нестаціонарна теплопровідність
Розглянемо знову дві посудини І і II, як для випадку нестаціонарної дифузії (див. рис. 5.3), об’єми яких відповідно рівні V1 і V2, але наповнюються тепер однорідним за складом газом при однаковому в обох посудинах тиску. Ці посудини з’єднані трубкою l з площиною перерізу s. Припустімо, що в деякий момент часу температури газу в цих посудинах дорівнюють Т1 і Т2, і для визначеності візьмемо Т1 > Т2.
Якщо на газ не діють
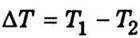
Зменшуватиметься з плином часу. Цей процес можна було б ще назвати “дифузією температури”. Принагідно сказати, що у цьому разі відбувається також дифузія в загальноприйнятому розумінні цього слова.
Знайдемо закон зменшення різниці температур з плином часу. Відповідно до рівняння (5.24) потік теплоти через трубку визначають рівнянням
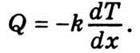
Припустімо також, що температура вздовж з’єднувальної трубки змінюється рівномірно,
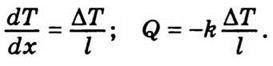
За нескінченно малий проміжок часу dt із посудини І у посудину II через трубку перейде кількість теплоти, яка дорівнює
Унаслідок цього температура газу в посудині І зменшиться на деяку величину dt1, а в посудині II підвищиться на величину dТ2. Ця зміна температур залежить від теплоємності газу СV, яка дорівнює добутку питомої теплоємності газу cV на його масу m. Із відомих співвідношень між кількістю теплоти і температурою зрозуміло, що
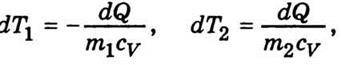
Де m1 і m2 – маси газу в посудинах І і II відповідно; dТ1 і dТ2 – абсолютні значення зміни температури.
Якщо густина газу в посудинах дорівнює ρ, то
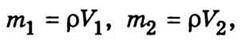
Тому можна записати попередні вирази у такому вигляді:
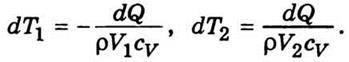
Зменшення температури в посудині І на dТ1 і збільшення її на dТ2 в посудині II приводить до зменшення різниці температур між ними на величину
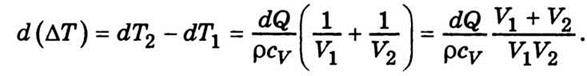
Підставивши сюди значення із співвідношення (5.25), дістанемо
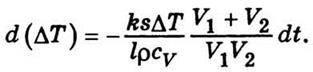
Позначимо, як і для дифузії, зведений об’єм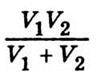 
через V0 перепишемо попередній вираз:
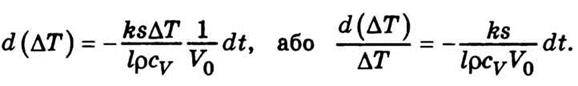
Зінтегрувавши цей вираз, матимемо
Де А – стала інтегрування. Її легко визначити, виходячи з тих міркувань, що різниця температур у початковий момент, тобто за t = 0, становить (ΔТ)0 . Підставивши у вираз (5.26) t= = 0 і ΔТ = (ΔТ)0, дістанемо А = (ΔТ)0. Отже,
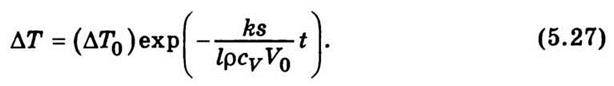
Рівняння (5.27) виражає закон вирівнювання температури з плином часу шляхом теплопровідності. Цей закон аналогічний закону вирівнювання концентрацій дифузією (5.17). В обох випадках вирівнювання відбувається за експоненціальним законом. Якщо порівняти (5.27) з (5.17)
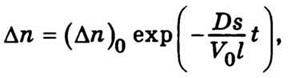
То видно, що експоненціальні множники в правій частині обох рівнянь збігаються за умови, що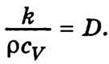 
Отже, вираз 
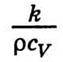можна вважати коефіцієнтом “дифузії температури”. Величина k/ρсV, яка залежить від властивостей газу, характеризує швидкість вирівнювання температури, тому вона називається коефіцієнтом температуропровідності газу (або будь-якого іншого тіла). Множник s/(V0l) є суто геометричним і характеризує лише апаратуру.
Неважко переконатися, що коефіцієнт температуропровідності так само, як і коефіцієнт дифузії, виражається в квадратних метрах на секунду (м2/с). Як і під час розгляду дифузії, введемо сталу часу теплопровідності τ, що є проміжком часу, протягом якого різниця температур між двома об’ємами внаслідок теплопровідності газу зменшиться в е разів,
(1 votes, average: 5.00 out of 5)
Loading...