Одночлени
261. Одночлени: 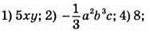
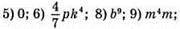
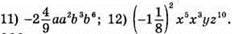
262. В стандартному вигляді записані: 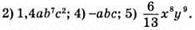
263. 1) 5а і 7a – подібні одночлени;
2) 3a2b2c і 6a2b2c – подібні одночлени;
3) 8х2у4 і 8х2у5 – не є подібними;
4) 3у2 і 2у3 – не є подібними;
5) 1/2m7n8 і 1/2m8n7 – не є подібними;
6) -0,1а°610 і 0,1а9610 – подібні одночлени.
264. 1) 5,6x3y7; 2) 4c4d10p2; 3) 5а5b5с9.
265. 1) 9а4аа6 = 9а11; 9 – коефіцієнт, 11 – степінь;
2) 3х • 0,4у • 6z = 7,2хyz; 7,2 – коефіцієнт, 3 – степінь;
3) 7а • (-9ас) = -63а2с; -63 – коефіцієнт,
4) 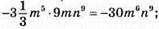 -30 – коефіцієнт, 15 – степінь;
-30 – коефіцієнт, 15 – степінь;
5) -5х2 • 0,1х2у • (-2у) = х4у2; 1 – коефіцієнт, 6 – степінь;
6) с • (-d) • с18 = – c19d; -1 – коефіцієнт, 20 – степінь.
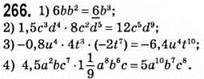
267. 1) Якщо x = -4, то 5×2 = 5 • (-4)2 = 5 • 16 = 80.
2) Якщо а = -1, b = 1/2, то
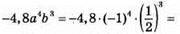
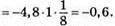
3) Якщо c = -10, d = 2, TO 0,04c3d5 = 0,04 • (-10)3 • 25 = 0,04 • (-1000) • 32 = -1280.
4) Якщо m = -3, n = 5, p = -1, то
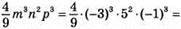
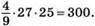
268. 1) Якщо m = -3, то 3m3 = 3 • (-3)3 = 3 • (-27) = -81.
2) Якщо a = -1/7, b = 2, то
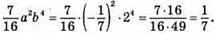
3) Якщо m = 0,3, n = 1/2, k = 2000, то
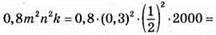
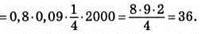
287. Нехай x – шукане число. Після зменшення на 10 % число дорівнює 0,9x. Після збільшення на 20 % число дорівнює 0,9x + 0,18x = 1,08х. 1,08x більше, ніж х, на 0,08x, або на 48 за умовою. Тому 0,08x = 48; х = 48 : 0,08; х = 600 – шукане число.
288. Нехай летіло х гусей.
Тоді х + х + 1/2х + 1/4х + 1 = 100; 2,75х = 99; х = 99 : 2,75; х – 36 гусей летіло в зграї.
289.
1) *5* ділиться націло на 3 і на 10.
150
450
750
2)13*2* ділиться націло на 9 і на 5.
13320
13725
3) 58* ділиться націло на 2 і на 3.
582
588