Степінь з натуральним показником. Одночлени
Урок № 29
Тема. Степінь з натуральним показником. Одночлени
Мета: узагальнити та систематизувати знання та вміння учнів, набуті в ході вивчення названої теми, підготовити учнів до тематичного оцінювання.
Обладнання: таблиця “Степінь. Властивість степеня”.
Тип уроку: узагальнення та систематизація знань та вмінь.
Хід уроку
I. Перевірка домашнього завдання
@ Цей етап уроку є ще аналізом самостійної роботи й корекцією вмінь. Тому бажано заздалегідь записати на дошці (або заготовити у вигляді індивідуального роздавального
II. Робота з випереджальним домашнім завданням
Систематизація та узагальнення знань учнів
@ У ході обговорення № 3 (випереджального домашнього завдання) з’ясуємо основні два блоки питань, що винесені на ТКР:
1) Означення і властивості степеня з натуральним показником.
2) Означення одночлена; одночлен стандартного вигляду; перетворення добутку одночленів та степеня одночлена в одночлен стандартного вигляду.
Оскільки таблиця 1 (див. урок 25), що узагальнює властивості степеня, уже складена, активно
Важливо дійти логіки, що об’єднує ці дві теми: використання саме властивостей степеня та вивчених раніше властивостей множення (переставної та сполучної) є основою тих перетворень одночленів, що винесеш на ТКР № 3.
III. Актуалізація опорних знань
Тестові запитання
1. Яка з рівностей є правильною:
1) n • n • n • n = 4n; 2) n • n • n • n = 4n; 3) n • n • n • n = n4?
2. Укажіть правильну рівність:
1) 54 • 53 = 512; 2) 54 • 53 = 2512; 3) (52)3 = 103; 4) (52)3 = 56.
3. Укажіть одночлени, записані у стандартному вигляді, а також їх коефіцієнти та степені таких одночленів:
1) 3a4 • 2b; 2) 0,7b14; 3) 5x2y3; 4) 2m • n • m.
4. Яка з рівностей є правильною:
1) 2а2b3 • 3а4 = 6а2b7;
2) 2а2b3 • 3а4 = 5а6b3;
3) 2а2b3 • 3а4 = 6a8b3;
4) 2a2b3 • 3а4 = 6a6b3?
@ Після виконання запропонованих вправ, виконуємо корекцію, під час якої повторюємо зміст основних понять теми й обов’язково звертаємо увагу на найтиповіші помилки (бажано не просто прокоментувати, а й спонукати учнів, які помилилися, до дії – придумати усні приклади на подібні властивості і, спираючись на відтворену властивість, правильно виконати їх).
Важливу роль у цій роботі відіграє наочність – таблиця “Степінь. Властивості степеня” (таблиця 1, урок 25) та таблиця 2.
Таблиця 2 |
Одночлен. Добуток і степінь одночлена |
1. Означення (неформальне). Добуток чисел, букв, їх степенів або число, або буква, або степінь є одночленом. |
Приклад: -3; b; а2; -32 •b – одночлени. |
2. Якщо в одночлені є один числовий множник, що записаний на першому місці, а також немає степенів з однаковою основою, то такий одночлен називається одночленом стандартного вигляду, а єдиний числовий множник – його коефіцієнтом. |
3. Множення одночленів: |
1) перемножте всі числові множники; |
2) перемножте окремо всі степені з однаковою основою; |
3) запишіть добуток числового множника з n. 1) на буквений множник(и) з n. 2) > утвориться шуканий одночлен – добуток. |
4. Піднесення одночлена до степеня: |
1) піднесіть до степеня кожний із множників, з яких складається одночлен; |
2) запишіть добуток утворених степенів та числових множників > утвориться Шуканий одночлен-степінь |
III. Засвоєння навичок
Подальша діяльність на уроці залежить від підготовки класу та результатів виконання попереднього виду роботи. Один із важливих варіантів – це організація роботи в групах, коли:
1) ті учні, які успішно виконали самостійну роботу (див. попередній урок) та виявили себе на уроці, виконуватимуть роль консультантів;
2) усі інші учні розподіляються на групи, виходячи з того, який пункт попереднього завдання викликав у них труднощі.
З такої точки зору можливе утворення груп:
I група – тема “Властивості степеня”;
II група – тема “Одночлен стандартного вигляду”;
ІІІ група – тема “Множення одночленів; піднесення до степеня”.
Кожна група отримує “консультанта” і завдання, яке треба розв’язати й презентувати через визначений учителем час.
Зміст завдань (див. додаток).
Обов’язково слід пам’ятати, що робота в групі означає активну участь кожного у спільному процесі, особливо звертати увагу на “слабких” учнів, залучати їх до роботи.
IV. Підсумки уроку. Рефлексія
Після презентації завдань кожної групи, спонукаємо учнів до рефлексії:
– Які поняття, теми, алгоритми зрозуміли добре, які – ні.
– Які теми та приклади за підручником треба опрацювати додатково?
V. Домашнє завдання
На підставі виконаної рефлексії із завдань 1-3-ї груп учні вибирають ті, що викликали труднощі, та розв’язують їх перед ТКР.
Додаток
Група 1. Тема “Властивості степеня”
1) Теорія (див. таблицю 1); 2) практичні завдання.
№ 1. Запишіть у вигляді степеня з основою х:
1) х5 • х3; 2) х4 • х; 3) (х5)3; 4) (x6)4.
№ 2. Запишіть у вигляді степеня:
1) (63 • 64)5 • 6; 2) (35 • 3)3 • (34)7; 3) 28 • 44 • 162.
№ 3. Запишіть у вигляді степеня з основою 2:
1) 22n • 4n+1 • (-16)2; 2) (8 • 22n+3)3 • (4п • 2n+2)2.
Група 2. Тема “Одночлен стандартного вигляду”
1) Теорія (див. таблицю 2); 2) практичні завдання.
№ 1. Подайте одночлен у стандартному вигляді:
L) 2a4 • 3a; 2) -0,3ab3 • 5a4b2.
№ 2. Спростіть вираз 3,6х2у2 • (-5х4у5) • (-2х2у).
№ 3. Знайдіть значення виразу (одночлена):
1) а8с4 • с4, якщо а = 4; с = -0,5;
2) 2 • x4y2z6 • х2 • у, якщо х = 2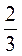 ; y = -2; z =
; y = -2; z = 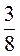 .
.
Група 3. Тема “Множення одночленів. Піднесення одночлена до степеня”
1) Теорія (див. таблицю 2); 2) практичні завдання.
№ 1. Виконайте дії з одночленами:
1) 2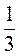 А2с3 • (3а2b4с3)3; 2) (-m7n8)5 • (-0,2m3n5)4.
А2с3 • (3а2b4с3)3; 2) (-m7n8)5 • (-0,2m3n5)4.
№ 2. Подайте одночлен 64а12b18 у вигляді:
1) добутку трьох різних одночленів стандартного вигляду;
2) добутку двох одночленів, одним з яких є -4а5b8;
3) куба одночлена стандартного вигляду.
№ 3. Знайдіть значення виразу:
1) (8m3n2)2 – n2, якщо m = 20, n = -0,025;
2) (3k+1аk)2 • (3аb)k • (bk)2, якщо а = 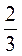 , b =
, b = 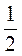 , k = 18.
, k = 18.
