Головна ⇒ 📌Довідник з геометрії ⇒ Описана піраміда
Описана піраміда
Геометрія
Комбінації геометричних тіл
Описана піраміда
Якщо вершина піраміди проектується в центр кола, яке є вписаним в основу піраміди, то центр вписаної кулі – точка перетину висоти піраміди з бісектрисою лінійного кута двогранного кута при ребрі основи.
У будь-яку правильну піраміду можна вписати кулю, центр якої лежить на висоті піраміди.
Точки дотику кулі й бічних граней лежать на висотах бічних граней, а точка дотику вписаної кулі й основи є центром кола, вписаного в основу.
Під час розв’язування задач на
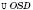 ;
; 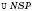 ;
; 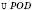 .
.O – центр кола, яке вписане в основу;
P – центр вписаної в піраміду кулі;
SO – висота піраміди;
SD – висота бічної грані.
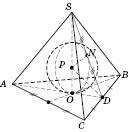
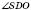 – лінійний кут двогранного кута між площиною бічної грані CSB і площиною основи;
– лінійний кут двогранного кута між площиною бічної грані CSB і площиною основи;DP – бісектриса
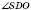 ;
;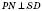 ;
;N – точка дотику кулі й бічної грані;
O
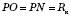 – радіус кулі;
– радіус кулі;OD – радіус кола, вписаного в основу, – rосн.
1. Розглянемо
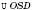 .
.За властивістю бісектриси трикутника
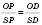 або
або 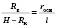 , де l – довжина апофеми.
, де l – довжина апофеми.2.
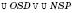 ;
;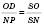 Або
Або 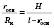 .
.3. Розглянемо
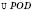 .
.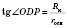
Related posts:
- Вписана та описана сфера 1. Нехай О А – радіус кулі, ОА = 1 см. АВ = ΚΚ1 = 2ОА = 2 см. CD = 2СО = 2 см. Sбіч. = PKLMN× КК1 = 4 × 2 × 2 = 16 (см2). Відповідь: 16 см2. 2. Нехай АВ =AD = ВВ1 = а. З ΔABD: З ΔΒ1BD: В1D2 = […]...
- Описані кулі Геометрія Комбінації геометричних тіл Описані кулі Кожна грань вписаного у сферу многогранника є вписаним у деяке коло многокутником. Основи перпендикулярів, які опущені з центра описаної кулі на площини граней, є центрами описаних навколо граней кіл. Отже, центром кулі, описаної навколо многогранника, є точка перетину перпендикулярів до площини граней, які проведені через центри кіл, описаних навколо […]...
- Піраміда. Площа поверхні та об’єм піраміди УРОК № 55 Тема. Піраміда. Площа поверхні та об’єм піраміди Мета уроку: повторити, привести в систему й розширити відомості про піраміди, площу поверхні та об’єм піраміди. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі пірамід. Вимоги до рівня підготовки учнів: пояснюють, що таке піраміда та її елементи; зображають і знаходять на […]...
- Вписані кулі Геометрія Комбінації геометричних тіл Вписані кулі Якщо куля вписана в призму, то в її перпендикулярний переріз можна вписати коло. Висота призми дорівнює діаметру кола, вписаного в перпендикулярний переріз призми, тобто діаметру вписаної кулі. Центр кулі – середина висоти призми, що проходить через центр кола, яке вписане в перпендикулярний переріз. Центр кулі, яка вписана в пряму […]...
- Прямокутний паралелепіпед. Піраміда Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 22. Прямокутний паралелепіпед. Піраміда Рис. 153 Коли ви були маленькими і гралися кубиками, то, можливо, складали фігури, зображені на рисунку 153. Ці фігури дають уявлення про прямокутний паралелепіпед. Форму прямокутного паралелепіпеда мають, наприклад, коробка цукерок, книга, цеглина, коробка сірників, пакувальний […]...
- Двогранні кути 520. Нехай дано двогранний кут, міра якого 60°, ∠AOB = 60°. AO + MN, BO + MN, АВ + β, АВ = 12 см. ΔАОВ – прямокутний. 521. Нехай дано двогранний кут, який дорівнює 45°. т. В? α, ОВ = 8 дм. АВ + β. Δ ΟΒΑ – прямокутний. 522. Нехай дано двогранний кут ∠BOA. […]...
- Багатогранники. Правильні багатогранники 3. Найменша кількість ребер, що сходиться в одній вершині багатогранника – три. 4. В одній вершині багатогранника може сходитися безліч ребер. Розглянемо піраміду з n-кутником в основі. Яким би великим не було число п, Завжди можна побудувати піраміду, основа якої має n + 1 вершин. 5. Розглянемо трикутну піраміду. Кількість її ребер шість. Шість – […]...
- Прямокутний паралелепіпед. Куб. Піраміда Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 25. Прямокутний паралелепіпед. Куб. Піраміда Сірникова коробочка, цеглина, дерев’яний брусок, ящик, пенал дають уявлення про геометричну фігуру, яка називається прямокутним паралелепіпедом (рис. 188). Рис. 188 Поверхня прямокутного паралелепіпеда складається із шести прямокутників, які називаються його гранями. Протилежні грані прямокутного паралелепіпеда попарно рівні. […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Комбінації тіл 1073. Нехай ABCDA1B1C1D1 – куб, вписаний в кулю з центром О, B1O = OD = 8 см. Тоді B1D = 2В1О = 2 × 8 = 16 (см). Відповідь: 16 см. 1074. Див. рис. 1075. Див. рис. 1076. Див. рис. 1077. Див. рис. 1078. Див. рис. 1079. Нехай ABCA1B1C1 – правильна трикутна призма. Sбіч. = […]...
- Многогранник Геометрія Многогранники Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається Опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини й поверхні опуклого многокутника називається Гранню. На рисунку нижче зліва зображений неопуклий многогранник; на рисунку справа – опуклий. […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
- Об’єм піраміди і зрізаної піраміди 1247. Нехай SABCD – правильна піраміда. SA = SB = SC = SD = AB = BC = CD = AD = 1 дм. З ΔACD: З ΔSAO: Знайдемо об’єм піраміди Відповідь: 1248. Нехай SABCD – правильна чотирикутна піраміда, SAC – діагональний переріз, SA = SC = AC = а. З ΔASO: Отже, об’єм піраміди: […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...
- Піраміди і зрізані піраміди 796. Нехай дано правильну чотирикутну піраміду, висота якої MO = 147 м, А площа основи – SABCD = 5,3 га = 53 000 м2. ∠MCO – кут нахилу бічного ребра. OK + ВС, MK + BC, ∠MKO – лінійний кут двогранного кута при ребрі основи піраміди. SABCD = 53 000 м2; ΔMOK – прямокутний. ∠MOK […]...
- Теорема Гульдіна 1379. У трикутнику ABC AB = ВС, AC = a, BK + AC, BK = h. Центром мас трикутника ABC є точка O – точка перетину медіан трикутника ABC: Тоді і Відповідь: 1380. ABCD – ромб, AB = a, ∠BAD = a, BD? I. SABCD = AB2 sin∠BAD = а2 sin α. Центром мас ромба […]...
- Властивості піраміди 1. 1) Оскільки піраміда за своїми властивостями має парну кількість ребер, то піраміда не може мати 13 ребер. 2) З’ясуємо, чи має система розв’язки. Розв’язків не має. Отже не існує піраміди, яка має 12 ребер і 6 граней. 2. SABCDEF правильна шестикутна піраміда. AB = BC = CD = DE = EE = AF = […]...
- Циліндр. Площа поверхні та об’єм циліндра УРОК № 56 Тема. Циліндр. Площа поверхні та об’єм циліндра Мета уроку: повторення, приведення в систему й розширення відомостей про циліндр, площу поверхні та об’єм циліндра; формування вмінь учнів знаходити площі поверхонь і об’єми циліндрів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі циліндрів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Піраміди 937. SΔABC = 30 см2. 938. ΔFMO: ∠О = 90°, OF = 4 см, ОМ = 3 см, FM = 5 см. 939. Δ ΟΡΕ: Ο = 90°, ∠Ε = 60°, ∠ΟΡΕ = 30°, ΡΕ = 10. ΟΕ = 5. DC = 2ΟΕ = 10, DC = 10. SABCD = 102= 100 (см2). 940. ΔOPE: […]...
- Куля Геометрія Тіла обертання Куля Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, […]...
- Тематична контрольна робота № 6 УРОК № 59 Тема. Тематична контрольна робота № 6 Мета уроку: перевірка навчальних досягнень учнів з теми “Початкові відомості зі стереометрії”. Тип уроку: контроль навчальних досягнень учнів. Вимоги до рівня підготовки учнів: застосовують означення та властивості геометричних фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 6 Тематичне оцінювання № 6 можна провести у […]...
- Тематична контрольна робота № 7 УРОК № 60 Тема. Тематична контрольна робота № 7 Мета уроку: перевірка навчальних досягнень учнів з курсу геометрії. Тип уроку: контроль навчальних досягнень учнів. Вимоги до рівня підготовки учнів: застосовують означення та властивості фігур при розв’язуванні задач. Хід уроку І. Тематичне оцінювання № 7 Тематичне оцінювання № 7 можна провести у вигляді тематичної контрольної роботи. […]...
- Многогранники Геометрія Многогранники Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує, – ребром двогранного кута. Півплощини називаються Гранями двогранного кута. Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох півпрямих. Кут, утворений такими півпрямими, називається Лінійним кутом двогранного кута (див. рисунок). За міру двогранного кута приймається міра його лінійного […]...
- Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...
- Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...