Головна ⇒ 📌ГДЗ з математики ⇒ Описане та вписане коло трикутника

Описане та вписане коло трикутника

§ 3. Паралельні прямі. Сума кутів трикутника

§ 20. Описане та вписане коло трикутника

540. 1) Різносторонній гострокутний трикутник.

Описане та вписане коло трикутника

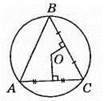
2) Прямокутний трикутник.

Описане та вписане коло трикутника

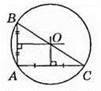
3) Тупокутний трикутник.

Описане та вписане коло трикутника

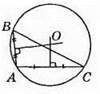
541. 1) Рівнобедрений гострокутний трикутник.

Описане та вписане коло трикутника

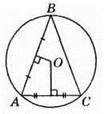
2) Рівнобедрений тупокутний трикутник.

Описане та вписане коло трикутника

542.

Описане та вписане коло трикутника

543.

Описане та вписане коло трикутника

544.

Описане та вписане коло трикутника

Вправи

545.

Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС (тому що вона є висотою). Тому точка О належить прямій BD.

Описане та вписане коло трикутника

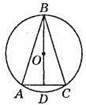
546. Висота ВН є також і бісектрисою, тому точка О належить прямій ВН.

Описане та вписане коло трикутника

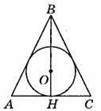
547. Нехай ВН – висота. Якщо точка O належить ВН, то ВН є бісектрисою (бо обидві точки В і О належать бісектрисі ∠В), отже, ?ABC – рівнобедрений.

548. Кожний серединний перпендикуляр до сторін рівностороннього трикутника є також бісектрисою.

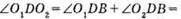
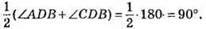
549. O1D і О2D – бісектриси кутів ADS i СDВ. Тому Описане та вписане коло трикутникаОписане та вписане коло трикутника

class=""/>

Відповідь: 90°.

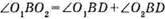
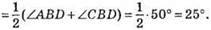
550. O1B і O2B є бісектрисами ∠ABD і ∠CBD. Тому Описане та вписане коло трикутникаОписане та вписане коло трикутника

Відповідь: 25°.

551. ?AEM = ?CEM (за двома катетами: ME – спільний катет, АЕ = СЕ, оскільки АС ⊥ ME). Із рівності трикутників випливає, що AM = MC.

Описане та вписане коло трикутника

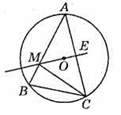
552. Р? ABC = АВ + ВС + АС = АМ + МВ + KB + КС + СЕ + ЕА = 8 + 2 + 2 + 4 + 4 + 8 = 28 (см) (бо AM = ЕА, СЕ = КС, MB = ВК – як відрізки дотичних, проведених з однієї точки до кола).

553. ВМ = ВК = 3 см – як відрізки дотичних, проведених з однієї точки до кола.

КС = СЕ = ВС – ВК = 8 – 3 = 5(см). АE = AM = AB – ВМ = 13 – 3 = 10 (см). Тоді АС = АЕ + СЕ = 10 см + 5 см = 15 см.

Відповідь: 15 см.

554. ВН ⊥ АС, тому ВН є серединним перпендикуляром до сторони АС, отже, AH = НС. Тому ВН є медіаною, отже, ?ABC – рівнобедрений.

Описане та вписане коло трикутника

555. Точка О належить бісектрисі кута ABC. Тому бісектриса кута є також і медіаною. Отже, ?ABC – рівнобедрений.

Описане та вписане коло трикутника

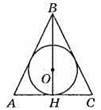
556. ?BOD = ?СОЕ (за катетом і гіпотенузою: BO = ОС, DO = OE), тому BD = CE. Оскільки AD = АЕ, маємо: AB =AD + BD = АЕ + CE = АС.

?AOD = ?COF (за катетом і гіпотенузою: АО = ОС, DO = OF), тому AD = CF. Оскільки BD = BF, маємо: AB = AD + BD = CF + BF = BC. Таким чином, AB = BC = АС, отже, ?ABC – рівнобедрений.

Описане та вписане коло трикутника

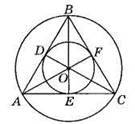
557. BD :DA = 7 : 5, P = 68 см.

Нехай AD = 5x CM, BD = 7 x см. Тоді AE = 5x см.

P? ABC = 2(AD + BD + AE) = 2(7x + 5x + 5x) = 34x. За умовою 34x = 68; x = 2. Отже, AB = AD + BD = 5x + 7x = 12x = 12 • 2 = 24 (см). BC = AD = 24 CM. AC = AE + EC = 5x + 5x = 10x = 10 • 2 = 20 (см).

Описане та вписане коло трикутника

Відповідь: 24 см, 24 см, 20 см.

558. Р? ABC = 52 см, AD : DB = 2 : 3, CF = 6 см.

Нехай AD = 2х см, DB = 3x см. Тоді BF = 3х см, ЕС = 6 см, АЕ = 2х см, AB = 5х см, ВС = (3х + 6) см, АС = (2х + 6) см.

5х + (3х + 6) + (2х + 6) = 52; 10х = 40; х = 4; 5х = 20; 3х + 6 = 18; 2х + 6 = 14.

Відповідь: 20 см, 18 см, 14 см.

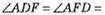
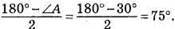
559. Нехай ∠A = 30°, ∠B = 70°, ∠C = 80°. AD = AF – як відрізки дотичних, проведених з однієї точки до кола, отже, ?ADF – рівнобедрений, Описане та вписане коло трикутникаОписане та вписане коло трикутника

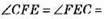
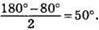
CF = CE – як відрізки дотичних, проведених з однієї точки до кола, отже, ?CFE – рівнобедрений, Описане та вписане коло трикутникаОписане та вписане коло трикутника

BD = BE – як відрізки дотичних, проведених з однієї точки до кола, отже, ?BED – рівнобедрений,

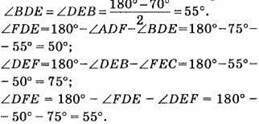
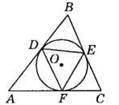
Описане та вписане коло трикутника

Описане та вписане коло трикутника

Відповідь: 50°, 75°, 55°.

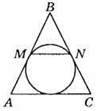
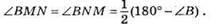
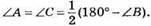560. BM = BN – як відрізки дотичних, проведені з однієї точки до кола. Отже, Описане та вписане коло трикутника

Описане та вписане коло трикутника Тому ∠BMN = ∠BAC як відповідні кути при прямих MN і АС і січній ВА. Отже, MN || АС.

Описане та вписане коло трикутника

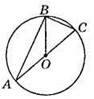
561. ОА = OB, отже, ∠A = ∠OBA, OB = ОС, отже, ∠C = ∠OBC. Тому ∠ABC = ∠A + ∠C. Але ∠A + ∠C = 180° – ∠ABC. ∠ABC = 180° – ∠ABC; 2∠ABC = 180°; ∠ABC=90°. Отже, ?АВС – прямокутний.

Описане та вписане коло трикутника

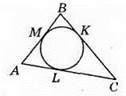
562. М, К, L – точки дотику, ВС = а. Оскільки BM = ВК, CK = CL – як відрізки дотичних, проведених з однієї точки до кола, то MB + CL = BK + CK = BC = а. Тоді Р? ABC = AM + AL + MB + BK +CK + CL. Оскільки BM = AL, то маємо P? ABC = 2AM + 2а. Звідси Р? ABC = 2р; 2АМ = 2р – 2а; 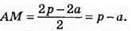Описане та вписане коло трикутника

Описане та вписане коло трикутника

563.

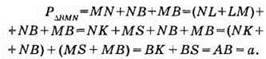
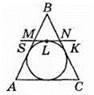
Описане та вписане коло трикутника

Описане та вписане коло трикутника

564. ?ABC – рівнобедрений (AB = BC), AC = 10 см.

Описане та вписане коло трикутника

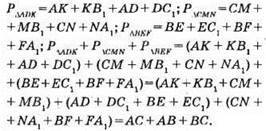
Оскільки сума периметрів трикутників ADK, BEF і CMN дорівнює 42 CM, TO маємо, AС + AB + BC = 42, 2AB = 32, AB = 16 (см).

Описане та вписане коло трикутника

Відповідь: 16 см.

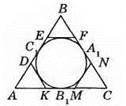
565. BD – медіана, BD = DC, AB = 7 см, ВС= 8 см.

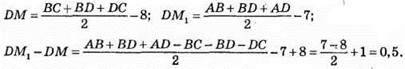
Описане та вписане коло трикутника

Описане та вписане коло трикутника

Відповідь: 0,5 см.

566. Розглянемо? АМС. AN, NC – бісектриси. Бісектриси трикутника перетинаються в одній точці, отже, MN – бісектриса кута М трикутника АМС. Тоді ∠AMN = ∠CMN.

Вправи для повторення

569. Оскільки BD – бісектриса кута ABC, то ∠ABD = ∠DBC.

Описане та вписане коло трикутника

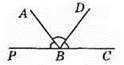
∠ABP = ∠ABD. Отже, ∠ABP + ∠ABD + ∠DBC =180°; ∠ABP = ∠ABD = ∠DBC = 180° : 3 = 60°, ∠ABD = 60° х 2 = 120°.

Відповідь: 120°.

570. ?ABC – рівнобедрений (AB = ВС), AH ⊥ BC, CL – бісектриса кута С. ∠HOC = 64°.

З? HОС: ∠H = 90°, ∠HOC = 64°, ∠HCO = 90° – 64° = 26°.

Описане та вписане коло трикутника

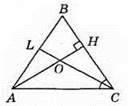
Оскільки CL – бісектриса, то ∠C = 26° х 2 = 52°, оскільки? BAC – рівнобедрений, то ∠A = ∠C = 52°. ∠В = 180° – ∠A – ∠C = 180° – 52° – 52° = 76°.

Відповідь: 52°, 52°, 76°.

571. AB = 3 см, ВС = 10 см, AK – бісектриса кута BAD.

Оскільки ВС || AD, то ∠KAD = ∠BKA, отже, ?ABC – рівнобедрений, BK = AB = 3 см, КС = ВС – ВК = 10 см – 3 см = 7 см.

Описане та вписане коло трикутника

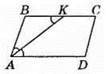
Відповідь: 3 см, 7 см.

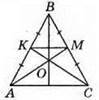
572. Оскільки? ABC – рівнобедрений, то КС і АМ є і бісектрисами.

Нехай ∠MAC = ∠KCA = α, тоді ∠AOC = ∠KOM = 180° – α, ∠CKM = ∠AMK = α. Отже, ∠MAC = ∠AMK = α. ∠MAC і ∠AMK – внутрішні різносторонні кути при прямих КМ і АС, і вони рівні, отже, КМ || АС.

Описане та вписане коло трикутника

573.

Описане та вписане коло трикутника


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Коло, описане навколо трикутника Урок № 49 Тема. Коло, описане навколо трикутника Мета: домогтися засвоєння учнями: – означення кола, описаного навколо трикутника; – властивостей вершин трикутника, вписаного в коло; – змісту теореми про коло, описане навколо трикутника, та схеми її доведення; – наслідку з теореми. Сформувати вміння: – відтворювати формулювання означення та теореми про коло, описане навколо трикутника; – […]...

  2. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  3. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  4. Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...

  5. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  6. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  7. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  8. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  9. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  10. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  11. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  12. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  13. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  14. Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, ­якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, ­якщо: – дві його висоти […]...

  15. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  16. НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...

  17. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  18. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  19. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  20. КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...

  21. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  22. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  23. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...

  24. Коло. Довжина кола Розділ 3 Відношення і пропорції §29. Коло. Довжина кола Дуже давно люди винайшли колесо та побачили його корисні в побуті властивості. Геометричними фігурами, які дають уявлення про колесо, є коло і круг. На малюнку 15 зображено креслярський інструмент – циркуль. На одній його ніжці – вістря, а на другій – грифель. Якщо поставити ніжку з […]...

  25. КОЛО І КРУГ Круг – перша найпростіша і найдосконаліша фігура. Прокл РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ У цьому розділі ви розширите і поглибите свої знання про коло і круг, набуті в попередніх класах, дізнаєтеся про взаємне розміщення на площині прямої і кола, двох кіл; про властивості дотичної до кола, дотичних кіл; про кола вписані й описані […]...

  26. Нерівність трикутника Геометрія Трикутники Нерівність трикутника Теорема. Які б не були три точки, відстань між будь-якими двома із цих точок не більша, ніж сума відстаней від них до третьої точки. Звідси випливає, що у будь-якому трикутнику кожна сторона менша за суму двох інших сторін, але більша за модуль різниці двох інших сторін. Якщо a, b і c […]...

  27. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  28. Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...

  29. Коло Урок № 41 Тема. Коло Мета: домогтися засвоєння учнями означень кола, круга та їх елементів. Сформувати вміння: – відтворювати означення кола та його елементів; – знаходити ці елементи на рисунку та виконувати рисунок за даним описом; – використовувати означення кола та його елементів під час розв’язування задач. Тип уроку: засвоєння знань, умінь і навичок. Наочність […]...

  30. КОЛО І КРУГ. КРУГОВИН СЕКТОР Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 16. КОЛО І КРУГ. КРУГОВИН СЕКТОР З усіх замкнених кривих ліній на площині найдосконалішою вважають коло. Якщо закріпити один кінець відрізка в якійсь точці, а потім повертати відрізок, то інший його кінець буде рухатися саме по колу. Тому кола зображують за допомогою циркуля (мал. 25). Мал. 25 Запам’ятайте! Коло […]...

  31. Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...

  32. Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...

  33. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  34. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  35. Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Цент­ром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...

  36. Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...

  37. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  38. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

  39. Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...

  40. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...

Ви зараз читаєте: Описане та вписане коло трикутника
«
»