Описані кулі
Геометрія
Комбінації геометричних тіл
Описані кулі
Кожна грань вписаного у сферу многогранника є вписаним у деяке коло многокутником. Основи перпендикулярів, які опущені з центра описаної кулі на площини граней, є центрами описаних навколо граней кіл. Отже, центром кулі, описаної навколо многогранника, є точка перетину перпендикулярів до площини граней, які проведені через центри кіл, описаних навколо граней.
Якщо призма вписана в кулю, то вона є прямою і навколо її основи можна описати коло.
Наприклад, довільна правильна
Навколо будь-якої правильної піраміди можна описати кулю. Центр її лежить на осі піраміди. Центр описаної навколо піраміди кулі може лежати всередині піраміди, поза пірамідою, на бічній грані, на основі.
Центр описаної навколо піраміди кулі – точка перетину перпендикуляра, проведеного до основи піраміди через центр описаного навколо основи кола, й серединного
Для правильної піраміди центр описаної кулі – це точка перетину прямої, яка містить висоту піраміди, й серединного перпендикуляра до бічного ребра.
Приклад
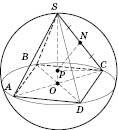
На рисунку SABCD – правильна чотирикутна піраміда, вписана у сферу. P – центр описаної кулі, PN – серединний перпендикуляр до бічного ребра.
(Зверніть увагу: якщо в умові задачі не задано, де лежить центр описаної кулі – усередині піраміди чи поза пірамідою, бажано розібрати, чи впливає це на розв’язання задачі та як саме.)
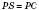 – радіус описаної кулі Rк.
– радіус описаної кулі Rк.OC – радіус кола, описаного навколо основи Rосн.
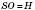 – висота піраміди.
– висота піраміди.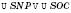 ;
;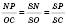 або
або 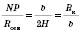 ;
;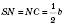 , де b – бічне ребро.
, де b – бічне ребро.Якщо зрізана піраміда вписана в кулю, то її основи – многокутники, навколо яких можна описати коло. Бічні грані такої зрізаної піраміди – рівнобічні трапеції. Отже, всі бічні ребра дорівнюють одне одному. Із цього випливає, що бічні ребра вихідної піраміди рівні, значить, основа висоти вихідної піраміди – центр кола, описаного навколо її основи.
Центр описаної кулі знаходимо так само, як і для повної піраміди.