Основні співвідношення між тригонометричними функціями одного й того самого кута

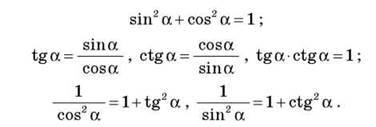
Related posts:

1. Співвідношення між тригонометричними функціями одного аргументу – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між тригонометричними функціями одного аргументу Для будь-якого Для будь-якого Для будь-якого Для будь-якого Для будь-якого...
2. Співвідношення між прямими й оберненими тригонометричними функціями – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між прямими й оберненими тригонометричними функціями...
3. Співвідношення між тригонометричними функціями одного аргументу УРОК 12 Тема. Співвідношення між тригонометричними функціями одного аргументу Мета уроку: вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь за­стосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження зна­чень тригонометричних функцій за однією відомою функцією. І. Аналіз контрольної роботи II. Мотивація навчання Дуже часто при розв’язуванні задач виникає проблема: зна­йти значення тригонометричних функцій, якщо […]...
4. ЗНАЧУЩІ ЧАСТИНИ СЛОВА. РОЗРІЗНЕННЯ СПІЛЬНОКОРЕНЕВИХ СЛІВ І ФОРМ ОДНОГО Й ТОГО САМОГО СЛОВА Мета: узагальнити знання учнів про морфемну будову слова; розвивати вміння знаходити основу, закінчення у слові, поданому в кількох граматичних формах, корінь у ряду поданих спільнокореневих слів, суфікс, префікс у ряду слів із тим самим суфіксом, префіксом; виховувати любов до рідного слова. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Словникова робота Гра “Склади […]...
5. Означення кута. Рiвнiсть кутiв. Бiсектриса кута. Вимiрювання та вiдкладання кутів Урок № 5 Тема. Означення кута. Рiвнiсть кутiв. Бiсектриса кута. Вимiрювання та вiдкладання кутів Мета: домогтися вiд учнiв засвоєння змiсту таких понять: “кут”, “елементи кута”, “позначення кута”, “внутрiшня область кута”, “промiнь, що дiлить даний кут на два кути”, “розгорнутий кут”, “рiвнi кути”, “бісектриса кута та аксiоми вимiрювання і вiдкладання кутiв”, “види кутiв”. Сформувати вмiння: – […]...
6. Кут. Вимірювання кутів. Бісектриса кута Розділ 1. Елементарні геометричні фігури та їхні властивості § 3. Кут. Вимірювання кутів. Бісектриса кута 33. 1) М – вершина кута, МА і МК – сторони кута АМК; 2) L – вершина кута, LP і LF – сторони кута PLF; 3) N – вершина кута, NB i NC – сторони кута BNC. 34. 1) O […]...
7. Тригонометричні функції кута УРОК 5 Тема. Тригонометричні функції кута Мета уроку: повторити означення тригонометричних функцій го­строго кута прямокутного трикутника і ввести озна­чення тригонометричної функції довільного кута. І. Аналіз помилок, допущених у математичному диктанті та самостійній роботі. 1. Побудуйте графіки функцій (індивідуальні картки): А) ; б) ; в) ; г) . Відповідь: а) рис. 25; б) рис. 26; в) […]...
8. ЯК ЗАЛЕЖИТЬ ОСВІТЛЕНІСТЬ ВІД КУТА ПАДІННЯ СВІТЛА? РОЗДІЛ 3. СВІТЛОВІ ЯВИЩА §24 . СИЛА СВІТЛА Й ОСВІТЛЕНІСТЬ 3. ЯК ЗАЛЕЖИТЬ ОСВІТЛЕНІСТЬ ВІД КУТА ПАДІННЯ СВІТЛА? Освітленість поверхні залежить не тільки від сили світла джерела та відстані до нього: вона ще залежить від кута падіння світла. І дуже істотно: саме цим, як ми зараз побачимо, зумовлено, наприклад, зміну пори року! У разі збільшення […]...
9. Величина кута. Вимірювання і побудова кутів Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 20.Величина кута. Вимірювання і побудова кутів Кути, як і відрізки, можна вимірювати. Поділимо прямий кут на 90 рівних частин (рис. 100). Міру однієї такої частини беруть за одиницю вимірювання кутів і називають градусом1. Позначають так: 1°. Градусна міра прямого кута дорівнює 90°, […]...
10. Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення при­лег­лого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...
11. Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Геометрія Декартові координати на площині Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Візьмемо коло на площині Oxy з центром у початку координат і радіусом R. Відкладемо від додатної півосі Ox кут у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо . Вона має координати . Тоді […]...
12. Синус, косинус і тангенс гострого кута прямокутного трикутника Урок № 54 Тема. Синус, косинус і тангенс гострого кута прямокутного трикутника Мета: домогтися засвоєння учнями змісту означень синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника та їх властивостей, що випливають із теореми Піфагора, подібності прямокутних трикутників та властивостей сторін прямокутного трикутника (проти більшої сторони лежить більший кут, і навпаки). Сформувати вміння відтворювати зміст […]...
13. Особливості того, як діє ринкова економіка РОЗДІЛ II Фундаментальні поняття ринкової економіки та ринкова інфраструктура Тема 2.1. Основні проблеми економіки та їх ринкове розв”язання 2. Особливості того, як діє ринкова економіка Ринкова економіка має особливі способи організації відносин економічних суб’єктів, які дозволяють забезпечувати упорядкованість і розвиток. Перший спосіб: в умовах ринку вибір того чи іншого варіанта використання ресурсів, тобто спрямованості виробництва, […]...
14. Співвідношення між коефіцієнтами лінійного та об’ємного розширення – Теплота й молекулярна фізика 6. Теплота й молекулярна фізика 6.9. Співвідношення між коефіцієнтами лінійного та об’ємного розширення β = 3а....
15. Метричні співвідношення в колі Урок № 38 Тема. Метричні співвідношення в колі Мета: домогтися засвоєння учнями змісту теорем про пропорційність відрізків хорд, пропорційність відрізків січної і дотичної та змісту наслідків (про відрізки січних, проведених з однієї точки кола) та їх доведення. Сформувати в учнів уміння: – відтворювати зміст вивчених теорем; – за готовими рисунками знаходити відрізки, про які йде […]...
16. Співвідношення між коефіцієнтами перенесення ФІЗИКА Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА Розділ 5 ЯВИЩА ПЕРЕНЕСЕННЯ 5.11. Співвідношення між коефіцієнтами перенесення Якщо порівняти вирази (5.18) і (5.22) для коефіцієнтів дифузії і в’язкості, то легко встановити, що вони між собою зв’язані таким співвідношенням: Величину η/ρ, як ми вже знаємо, називають кінематичною в’язкістю. Вона має таку саму розмірність, що й коефіцієнт дифузії, […]...
17. Лабораторна робота № 8. Внутрішня будова листка у зв’язку з його функціями Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 12* Тема. Лабораторна робота № 8. Внутрішня будова листка у зв’язку з його функціями Мета. Ознайомитися з внутрішньою будовою листка та його структурними елементами у зв’язку з функціями, які вони виконують. Обладнання: листки кімнатних рослин, мікропрепарат “Поперечний розріз листка”, мікроскоп, […]...
18. Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 8 * Тема. Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Мета. Розширити знання учнів про анатомічну будову кореня у зв’язку із функціями, що вони виконують. Основні поняття і терміни: кореневий чохлик, зона ділення, зона росту, […]...
19. Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
20. Співвідношення невизначеностей ФІЗИКА Частина 5 АТОМНА ФІЗИКА Розділ 16 ХВИЛЬОВІ ВЛАСТИВОСТІ РЕЧОВИНИ 16.5. Співвідношення невизначеностей На відміну від класичних частинок мікрочастинкам одночасно притаманні хвильові й корпускулярні властивості. В одних випадках вони поводять себе як хвилі, а в інших – як окремі корпускули. Наявність хвильових властивостей у мікрочастинок, які не можна пояснити з погляду класичної механіки, приводить до […]...
21. Співвідношення між сторонами і кутами прямокутного трикутника Урок № 59 Тема. Співвідношення між сторонами і кутами прямокутного трикутника Мета: домогтися засвоєння учнями змісту правил знаходження невідомих сторін прямокутного трикутника, що випливають з означень тригонометричних функцій гострого кута; формувати вміння відтворювати зміст цих правил, а також застосовувати правила для знаходження невідомих сторін прямокутного трикутника. Закріплювати знання числових значень тригонометричних функцій кутів 30°, 45°, […]...
22. Закон Авогадро. Молярний об’єм газу. Об’ємні співвідношення газів у реакціях ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ І. ЗАГАЛЬНА ХІМІЯ 1. Основні хімічні поняття. Речовина 1.8. Закон Авогадро. Молярний об’єм газу. Об’ємні співвідношення газів у реакціях Італійський учений А. Авогадро звернув увагу на те, що всі гази однаково стискуються (закон Бойля – Маріотта1), мають однаковий термічний коефіцієнт розширення (закон Гей-Люссака2) та деякі інші […]...
23. Перехід з одного виду пенсії на інший Перехід з одного виду пенсії на інший – перехід, який може мати місце щодо осіб, які водночас мають право на різні державні пенсії. їм призначається одна пенсія за вибором. Винятком є пенсія інвалідам внаслідок поранення, контузії чи каліцтва, що їх вони дістали при захисті Батьківщини або при виконанні інших обов’язків військової служби, або внаслідок захворювання, […]...
24. ЗАКОНИ ЗОВНІШНЬОГО ФОТОЕФЕКТУ. СПІВВІДНОШЕННЯ ЕЙНШТЕЙНА – ФОТОЕФЕКТ – СВІТЛОВІ КВАНТИ Фізика підготовка до ЗНО комплексне видання КВАНТОВА ФІЗИКА. ЕЛЕМЕНТИ ТЕОРІЇ ВІДНОСНОСТІ 2. СВІТЛОВІ КВАНТИ 2.2. ФОТОЕФЕКТ 2.2.2. ЗАКОНИ ЗОВНІШНЬОГО ФОТОЕФЕКТУ. СПІВВІДНОШЕННЯ ЕЙНШТЕЙНА Закони зовнішнього фотоефекту 1. Максимальна початкова швидкість фотоелектронів залежить лише від частоти світла і властивостей поверхні металу. 2. Число електронів п, які вириваються світлом за одиницю часу, прямо пропорційне освітленості металу (n – […]...
25. Основні тригонометричні тотожності – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні тотожності...
26. Чи розуміють тварини одне одного? ЗАПИТАННЯ ДО ПРИРОДИ УРОК 62 Чи розуміють тварини одне одного? Тема. Чи розуміють тварини одне одного? Мета: сприяти розвитку пізнавального інтересу учнів; розвивати бажання більше знати, прагнення з’ясовувати невідоме; сприяти вихованню любові до живого світу природи. ХІД УРОКУ I. Організаційний момент II. Повідомлення теми і мети уроку – Як відомо, тварини не можуть розмовляти, як […]...
27. ОСНОВНІ ОРФОГРАМИ ДОДАТКИ Додатки 3 ОСНОВНІ ОРФОГРАМИ 1. Букви е, и, що позначають ненаголошені голосні в коренях слів. 2. Велика буква у власних назвах. 3. Букви, що позначають звуки, які уподібнюються. 4. Подвоєні букви. 5. Роздільне написання прийменників з іменниками і займенниками. 6. Перенос частин слова з рядка в рядок. 7. Уживання м’якого знака. 8. Уживання апострофа. […]...
28. Співвідношення між рівністю доходів і соціальною справедливістю Співвідношення між рівністю доходів і соціальною справедливістю – взаємозалежність між рухом соціально-економічної системи до вирівнювання доходів між найбагатшими і найбіднішими верствами населення (а отже, подолання нерівності) і урівноваженістю між правами та обов’язками людей, між кількістю та якістю праці і розміром отримуваних реальних доходів та ін. Проблему нерівності доходів Р.-К. Макконнелл і С.-Л. Брю пов’язують з […]...
29. Спілкування як сприймання та розуміння одне одного – ПСИХОЛОГІЧНА ПРИРОДА СПІЛКУВАННЯ ЕТИКА ДІЛОВОГО СПІЛКУВАННЯ Лекція 4 ПСИХОЛОГІЧНА ПРИРОДА СПІЛКУВАННЯ Спілкування як сприймання та розуміння одне одного Взаємодія між учасниками спілкування, як правило, супроводжується сприйманням і розумінням одне одного. Деякі психологи вважають, що відбувається пізнання однієї людини іншою. У загальному плані можна сказати, що сприймання іншої людини означає відображення її зовнішніх ознак, співвіднесення їх з особистісними характеристиками […]...
30. Основні поняття фотометрії ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 11 ОСНОВИ ФОТОМЕТРІЇ. ОСНОВНІ ЗАКОНИ ГЕОМЕТРИЧНОЇ ОПТИКИ 11.1. Основні поняття фотометрії Дія світла зумовлена насамперед наявністю певної світлової енергії. Безпосередньо світло, зумовлене дією світлової енергії, сприймається чутливими елементами ока. Те саме відбувається в будь-якому приймачі, здатному реагувати на світло, наприклад у фотоелементі, термоелементі, фотопластинці. Саме вимірювання світла […]...