Ознаки паралельності двох прямих
§ 3. Паралельні прямі. Сума кутів трикутника
13. Ознаки паралельності двох прямих
Практичні завдання
300. 1) Кути АОМ і CEO – відповідні;
2) кути АОЕ і СЕК – відповідні;
3) кути АОE і OED – різносторонні;
4) кути АОЕ і CEO – односторонні.
1) відповідні; 2) односторонні; 3) різносторонні.
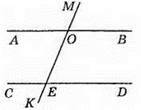
301. 1) ∠1 i ∠5; ∠2 i ∠6; ∠3 i ∠7; ∠4 i ∠8;
2) ∠3 i ∠6; ∠4 i ∠5;
3) ∠3 i ∠5; ∠4 i ∠6.
Вправи
302. Різносторонні кути: ∠MKT і ∠KTD; ∠EKR і ∠KTS.
Односторонні кути: ∠MKT
Відповідні кути: ∠CKM і ∠KTS; ∠TKM і ∠OTS; ∠CKE і ∠KTD; ∠TKE і ∠OTD.
303. 1) ∠CBA і ∠BAD; 2) ∠DEC і ∠EDC; 3) ∠BCE і ∠CED; 4) ∠CEA і ∠CDA; 5) ∠BCE і ∠AEC.
304. 1) а || b; 2) а || b; 3) а || b; 4) а || b.
305. 1) Так; 2) так; 3) так; 4) ні; 5) так; 6) так.
306. 1) m || n; 2) m || n; 3) m || n; 4) m || n.
307. а || d, b || m.
308. а || с.
309. ?ABC i? CDK – рівнобедрені, тоді ∠BAC = ∠BCA, ∠KCD = ∠CKD. Оскільки ∠BCA = ∠KCD (як вертикальні), маємо ∠BAC = ∠CKD – внутрішні різносторонні при прямих AB і DK та січній AK. Отже, AB || DK.
310. ?АМК – рівнобедрений, тому ∠MAK = ∠MKA. Крім того ∠MAK = ∠KAC (бо АК – бісектриса). Тоді ∠MKA = ∠KAC (а ці кути внутрішні різносторонні при
311. ?ADC – рівнобедрений, тому ∠CAD = ∠ACD, крім того ∠ACD = ∠ACB за умовою, тому ∠ACD = ∠ACB. Оскільки ∠ACD і ∠CAD – внутрішні різносторонні кути при прямих ВС і AD та січній АС, то ВС || AD.
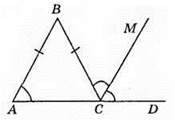
312. На рисунку АВ = ВС, ∠А = 60°, тоді ∠ACB = ∠A = 60°. ∠BCD = 180° – ∠ACB = 180° – 60° = 120°, ∠MCD = 1/2∠BCD = 1/2 • 120° = 60°.
Оскільки ∠ВАС = ∠MCD і ці кути є відповідними між прямими AB і CM та січною AD, то AB || CM.
313. На рисунку AO = BO, CO = OD, ∠COA = ∠DOB – як вертикальні кути, тоді? АОС = ?BOD (за двома сторонами 1 кутом між ними). Із рівності цих трикутників випливає, що ∠1 = ∠2. Оскільки∠1 = ∠2 і ці кути є внутрішніми різносторонніми при прямих АС і BD та січній AB, то АС || BD.
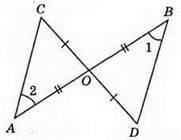
314. ?ABD = ?CDB (за третьою ознакою: AB = CD за умовою, ВС = AD за умовою, BD – спільна). Із рівності трикутників маємо: ∠ABD = ∠CDB – це внутрішні різносторонні кути при прямих AB іCD та січній BD, отже, AB || CD.
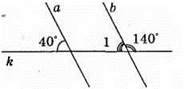
315. Оскільки ∠1 = 180° – 140° = 40°. Кути 40° і 1 – відповідні кути при прямих а і b та січній k, тоді a || b.
Якщо деяка пряма m перетинає пряму а, то пряма m теж буде перетинати і пряму b, бо а || b.
316. Кути ВАС і DCA – різносторонні при прямих AB і CD та січній АС, ∠BAC + ∠DCA = 48° + 132° = 180°, то AB || CD. Кути BAF і AFE – внутрішні різносторонні при прямих AB і EF та січній AF,∠BAF = 48° + 24° = 72° = ∠AFE, то AB || EF.
Оскільки AB || CD і AB || EF, то CD || EF.
317. Якщо ∠ABC = 60°, ∠BCD = 120°, TO не завжди AB || CD.
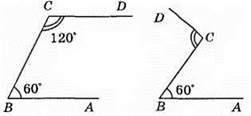
Відповідь: ні.
318. Якщо кут між прямими а і с дорівнює куту між прямими b і с, то не завжди a || b.
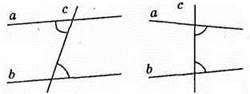
319. Ні.
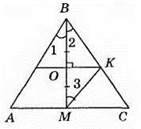
320. На рисунку: ∠1 = ∠2, ВО = ОМ, ВМ ⊥ ОК. ?ВКМ – рівнобедрений (бо в ньому співпадає висота і медіана ОК), тоді ∠3 = ∠2 = ∠1. Оскільки ∠3 і ∠1 – внутрішні різносторонні при прямих AВ і МК та січній ВМ, то AВ || МК.
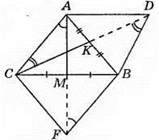
321. ?BMF = ?CMА – за двома сторонами і кутом між ними (ВМ = CM за умовою, MF = AM за умовою, ∠FMB = ∠AMC – як вертикальні). Із рівності трикутників маємо: ∠BFM = ∠CAM, тоді AC ||FB.
?АСК = ?BDK – за двома сторонами і кутом між ними (АК = ВК за умовою, СК = KD за умовою, ∠AKC = ∠BKD – як вертикальні кути). Із рівності трикутників маємо: ∠ACK = ∠BDK, тоді AC || BD.
Оскільки АС || FB і АС || BD, то згідно з аксіомою паралельності прямих, FB і BD співпадають. Отже, точки В, D, F лежать на одній прямій.
Вправи для повторення
322. І випадок: ∠AOC : ∠BOC = 3:5, тоді ∠AOC = 3х°, ∠BOC = 5х°. За умовою ∠BOC – ∠AOC = 42°, 5x – 3x = 42; 2x = 42; х = 21. Тоді ∠AOC = 3 х 21° = 63°, ∠BOC = 5 x 21° = 105°. ∠DOB = 180° = 63° – 105° = 12°.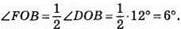 
∠FOC = ∠FOB + ∠BOC = 6° + 105° = 111°.
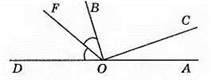
II випадок: ∠AOD = 180° – 105° – 63° = 12°;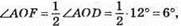 
∠FOC = ∠FOA + ∠AOC = 6° + 63° = 69°.
Відповідь: 111° або 69°.
323. Оскільки AB = ВС, то ∠A = ∠C. Оскільки ∠ABK = ∠CBM, то ∠ABM = ∠ABK – ∠MBK = ∠CBM – ∠MBK = ∠KBC.
?АВМ = ?СВК за стороною і двома прилеглими кутами (AB = ВС за умовою, ∠A = ∠C – за доведеним, ∠ABM = ∠KBC – за доведеним). Із рівності трикутників випливає: ВМ = ВК.
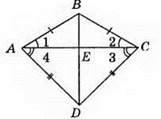
324. Оскільки? AВС і? АDС – рівнобедрені, то ∠1 = ∠2, ∠3 = ∠4, тоді ∠BAD = ∠1 + ∠4 = ∠2 + ∠3 = ∠BCD. ?BAD = ?BCD – за першою ознакою, із рівності трикутників маємо: ∠ABE = ∠CBE. Оскільки? ABC – рівнобедрений і BE – бісектриса, то BE – медіана, отже, АЕ = ЕС.
Спостерігайте, рисуйте, конструюйте, фантазуйте.
325. Чотирикутник KLMN і трикутник ABC мають спільну частину – восьмикутник.
(1 votes, average: 5.00 out of 5)
Loading...