Паралельне перенесення в просторі
Урок 49
Тема. Паралельне перенесення в просторі
Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач.
Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда.
Хід уроку
І. Перевірка домашнього завдання
1. Перевірити правильність розв’язування задачі № 19 за готовими записами на дошці.
Нехай А(хА; уА; zА), В(хB; yB; zB) – дані
Знайдемо довжину відрізка АВ: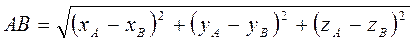 
.
Точки A1 і В1 – симетричні точкам А і В відносно точки С, тоді
А1 (2xC – хA; 2уC – yA; 2zC – zA),
B1 (2xC – хB; 2уC – yB; 2zC – zB).
Знайдемо довжину відрізка А1B1: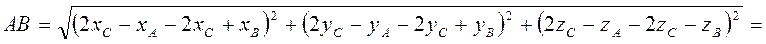 
.
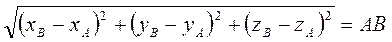Отже, перетворення симетрії відносно точки є рухом.
2. Самостійна робота.
Варіант 1
1) Кінці відрізка А(3; 1; 8) і В (5; 7; 2). Знайдіть точку, симетричну середині відрізка відносно площини xz. (6 балів)
2) Точки А (4; 2; 10), B(10; -2; 8), С(-2; 0; 6) – вершини паралелограма ABCD. Знайдіть координати вершини D.
1) Кінці відрізка А (5; -2; 1) і В (5; 4; 5). Знайдіть точку, симетричну середині відрізка відносно початку координат. (6 балів)
2) Точки В (2; 1; 3), C(1; 1; 4), D(0; 1; 3) – вершини паралелограма ABCD. Знайдіть координати вершини А. (6 балів)
1) Кінці відрізка А (7; -3; 4) і B(-1; -1; 2). Знайдіть точку, симетричну середині відрізка відносно осі X. (6 балів)
2) Точки A(2; 1; 3), C(2; 1; 5), D (0; 1; 1) – вершини паралелограма ABCD. Знайдіть координати вершини В. (6 балів)
1) Кінці відрізка А(2; 1; 3) і В(6; 1; 5). Знайдіть точку, симетричну середині відрізка відносно площини ху. (6 балів)
2) Точки А (4; 2; -1), В (-4; 2; 1) і D(7; -3; 4) – вершини паралелограма ABCD. Знайдіть координати вершини С. (6 балів)
Відповідь. Варіант 1. 1) (4;-4;5); 2) D(-8;4;8). Варіант 2. 1) (-5;-1;-3); 2) A(1;1;2). Варіант 3. 1) (3;2;-3); 2) B(4;1;7). Варіант 4. 1) (4;1;- 4); 2) С(-1;-3;6).
Паралельним перенесенням у просторі називається таке перетворення, при якому довільна точка (х; у; z) фігури переходить у точку (х+ а; у + b; z + с), де числа а, b, с – одні і ті самі для всіх точок. Паралельне перенесення в просторі задають формулами: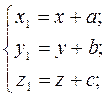 
Що виражають координати х1, у1, z1 точки, в яку переходить точка (х; у; z) при паралельному перенесенні.
1. Паралельне перенесення задається формулами: х1 = х +3, y1 = у – 3, z1 = z + 1. В яку точку при цьому паралельному перенесенні переходить точка А(1;2;3) ?
2. Паралельне перенесення задається формулами: х1 = x + 1, у1 = у + 2, z1 = z +3. Точка А при цьому перенесенні переходить у точку В (2; 3; 1). Знайдіть координати точки А.
3. Точка А (1; 2; 3) при паралельному перенесенні переходить у точку В (3;2,1). Запишіть формули цього паралельного перенесення.
4. Чи існує паралельне перенесення, при якому точка А (1; 3; 2) переходить у точку В (0; 2; 4), а точка D (2; 2; 2) переходить у точку C (1; 1; 4)?
Властивості паралельного перенесення
1. Паралельне перенесення є рух.
2. При паралельному перенесенні пряма переходить у паралельну їй пряму (або в себе).
3. При паралельному перенесенні площина переходить або в себе, або у паралельну їй площину.
4. Які б не були дві точки А і А’, існує єдине паралельне перенесення, в результаті якого точка А переходить у точку А’. Учні самостійно знайомляться з доведенням властивості 3 за підручником.
Розв’язування задач
1. Побудуйте фігуру, в яку переходить куб при паралельному перенесенні, при якому точка А переходить у точку В (рис. 269).
2. Задача № 26 із підручника (с. 56).
3. Задача № 27 із підручника (с. 56).
III. Домашнє завдання
§4, п. 29; контрольні запитання № 9-11; задачі № 23, 24, 25 (1) (с. 56).
IV. Підведення підсумку уроку
Запитання до класу
1) Дайте означення паралельного перенесення.
2) Перелічіть основні властивості паралельного перенесення.
3) При паралельному перенесенні точка А (1;-1; 0) переходить у точку B(3;-1;2). Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) дане паралельне перенесення задається формулами x1 = х + 2 , y1 = у, z1 = z + 2;
Б) початок координат при даному паралельному перенесенні переходить у точку (-2; 0; – 2);
В) точка В при даному паралельному перенесенні переходить у точку (5; -1; 4);
Г) паралельні перенесення, при якому точка В переходить у точку А, задається формулами x1 = x + 2 , y1 = y + 2 , z1 = z + 3.
(1 votes, average: 5.00 out of 5)
Loading...