Паралельні прямі
Геометрія
Основні властивості найпростіших геометричних фігур
Паралельні прямі
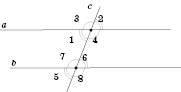
На рисунку зображені кути, утворені в результаті перетину двох прямих січною:
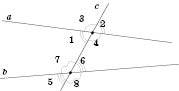
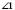 і
і 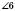 ;
; 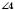 і
і 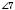 – внутрішні різносторонні кути при прямих a, b і січній c.
– внутрішні різносторонні кути при прямих a, b і січній c.
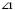 і
і 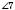 ;
; 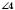 і
і 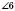 – внутрішні односторонні.
– внутрішні односторонні.
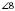 ;
; 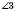 і
і 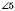 – зовнішні односторонні.
– зовнішні односторонні.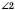 і
і 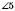 ;
; 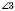 і
і 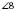 – зовнішні різносторонні.
– зовнішні різносторонні.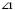 і
і 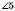 ;
; 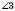 і
і 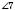 ;
; 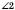 і
і 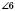 ;
; 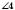 і
і 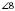 – відповідні.
– відповідні.Властивості паралельних прямих
Теорема 1. Якщо дві паралельні
1) внутрішні різносторонні кути рівні;
2) сума внутрішніх односторонніх кутів дорівнює
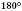 ;
;3) зовнішні різносторонні кути рівні;
4) сума зовнішніх односторонніх кутів дорівнює
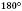 ;
;5) відповідні кути рівні.
На рисунку позначені числами чотири пари кутів. Теорема стверджує, що, якщо
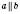 , то
, то 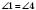 ,
, 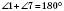 ;
; 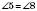 ;
; 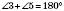 ;
; 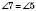 :
:
Теорема 2. Якщо пряма перпендикулярна до однієї з паралельних прямих, то вона перпендикулярна і до другої.
Теорема 3. Через точку, що не лежить на прямій, можна провести пряму, паралельну даній.
Об’єднуючи це твердження з аксіомою IX, отримуємо: через точку, що не лежить на прямій, можна провести пряму, паралельну даній, причому тільки одну.
Ознаки паралельності прямих
Теорема 1. Якщо при перетині двох прямих третьою виконується хоча б одна з таких умов:
а) внутрішні різносторонні кути рівні;
б) сума внутрішніх односторонніх кутів дорівнює 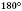 ;
;
в) зовнішні різносторонні кути рівні;
г) сума зовнішніх односторонніх кутів дорівнює 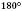 ;
;
д) відповідні кути рівні,- то прямі паралельні.
Теорема 2. Дві прямі, паралельні третій, паралельні одна одній.
Теорема 3. Дві прямі, перпендикулярні до третьої, паралельні одна одній.
Related posts:
- Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...
- Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...
- Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...
- Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...
- Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
- ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 5. ПЕРПЕНДИКУЛЯРНІ І ПАРАЛЕЛЬНІ ПРЯМІ Пригадайте, як можуть розташовуватися на площині дві прямі. Якщо вони перетинаються, то утворюють чотири кути – дві пари вертикальних кутів. Йдеться про кути, менші від розгорнутого. Менший із цих кутів вважають кутом між даними прямими. Наприклад, на малюнку 56 прямі АВ і […]...
- Паралельні прямі Розділ 4 Раціональні числа і дії мідними §52. Паралельні прямі Дві різні прямі, побудовані на аркуші паперу або дошці, можуть перетинатися в одній точці (мал. 104) або не перетинатися (мал. 105). Аркуш паперу, дошка дають уявлення про площину. Також уявлення про площину дають поверхня стола, шибка тощо. Мал. 104 Мал. 105 Мал. 106 – Дві […]...
- Паралельні прямі. Властивості паралельних прямих Урок № 110 Тема. Паралельні прямі. Властивості паралельних прямих Мета: закріпити знання учнів про властивості паралельних прямих; відпрацювати навички розв’язування задач, що передбачають застосування набутих з теми знань; продовжувати роботу з повторення вивченого у 6 класі матеріалу. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Математичний диктант […]...
- ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...
- Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...
- ПЕРПЕНДИКУЛЯРНІ ТА ПАРАЛЕЛЬНІ ПРЯМІ Розділ 5 ВИРАЗИ І РІВНЯННЯ § 33. ПЕРПЕНДИКУЛЯРНІ ТА ПАРАЛЕЛЬНІ ПРЯМІ Ви знаете, що пряма – це геометрична фігура. Дві прямі можуть по-різному розмішуватись на площині. У 6 класі ви дізнаєтеся про перпендикулярні та паралельні прямі. 1. Перпендикулярні прямі Подивиться на перехрестя доріг на малюнку 143. Вибачите, що дороги нагадують прямі, які перетинаються, утворюючи чотири […]...
- Паралельні прямі Урок № 109 Тема. Паралельні прямі Мета: сформувати уявлення про зміст поняття “паралельні прямі”; виробити вміння знаходити на рисунку паралельні прямі та будувати за допомогою косинця і лінійки пряму, паралельну до даної, що проходить через точку поза даною прямою. Тип уроку: засвоєння нових знань. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Перевіряємо […]...
- Суміжні й вертикальні кути Геометрія Основні властивості найпростіших геометричних фігур Суміжні й вертикальні кути Два кути називаються Суміжними, якщо в них одна сторона спільна, а інші сторони є доповняльними півпрямими. На рисунку і – суміжні. Властивості суміжних кутів Теорема 1. Сума суміжних кутів дорівнює . (Зверніть увагу: кути, сума яких дорівнює , не обов’язково суміжні.) Теорема 2. Коли два […]...
- Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...
- Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...
- Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...
- Перпендикулярні прямі Урок № 108 Тема. Перпендикулярні прямі Мета: закріпити знання учнів про поняття перпендикулярних прямих та їх властивості; відпрацювати навички розпізнавати та будувати перпендикулярні прямі за допомогою косинця та застосовувати ці навички під час розв’язування завдань творчого характеру (на просторову уяву); повторити властивість вимірювання кутів, розв’язання задач та складання рівнянь. Тип уроку: застосування знань, умінь, навичок. […]...
- Вертикальні кути Розділ 1. Найпростіші геометричні фігури та їх властивості § 5. Вертикальні кути 152. 1) ∠AYX і ∠BYZ – вертикальні; 2) ∠OLK і ∠MLN – не вертикальні. 153. 1) ∠AOD – вертикальний з кутом 1; 2) ∠АОС і ∠DOB – суміжні з кутом 1. 154. ∠BOA і ∠COD – суміжні. ∠BOA = ∠COD = 60°. 155. […]...
- Перпендикулярні та паралельні прямі. Координатна площина. Графіки залежностей Урок № 118 Тема. Перпендикулярні та паралельні прямі. Координатна площина. Графіки залежностей Мета: підготувати учнів до виконання до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Задачу № 2 перевіряємо фронтально, бо вона є нестандартною, за описом треба зробити графік (див. рис […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Ознаки паралельності прямих Урок № 30 Тема. Ознаки паралельності прямих Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною). Сформувати вміння: – визначати вид двох кутів, що утворилися при перетині двох прямих січною; – за певним співвідношенням цих кутів робити висновок щодо паралельності прямих; – для встановлення співвідношення кутів […]...
- ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 7. ВЛАСТИВОСТІ ПАРАЛЕЛЬНИХ ПРЯМИХ ЗАДАЧА Дано пряму а і точку Р, що не належить цій прямій. Проведіть через точку Р пряму, паралельну прямій а. – За допомогою лінійки і косинця побудову можна виконати, як показано на малюнку 90. Чи можна через точку Р провести дві різні прямі, […]...
- Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Перпендикулярні прямі Розділ 4 Раціональні числа і дії мідними §51. Перпендикулярні прямі Дві прямі, що мають одну спільну точку, називають прямими, що перетинаються. Їх спільну точку називають точкою перетину. На малюнку 89 прямі а і b перетинаються, М – точка їх перетину. Дві прямі, перетинаючись, окрім розгорнутих, утворюють чотири кути зі спільною вершиною, градусна міра яких менша […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- ТЕОРЕМИ І АКСІОМИ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 8. ТЕОРЕМИ І АКСІОМИ Ви вже маєте уявлення про теореми. Теорема – це твердження, в істинності якого переконуються за допомогою логічних міркувань, доведень. Звичайно теорема містить умову (те, що дано) і висновок (що вимагається довести). Щоб виокремити умову і висновок теореми, її зручно подати у формі “Якщо…, […]...
- Вертикальні кути. Кут між двома прямими, що перетинаються Розділ 2. Взаємне розміщення прямих па площині § 6. Вертикальні кути. Кут між двома прямими, що перетинаються 107. 1) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 15°, дорівнює 15°. 2) За властивістю вертикальних кутів – вертикальні кути рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°. Відповідь: 1) 15°; […]...