Перетворення подібності та його властивості
Урок 50
Тема. Перетворення подібності та його властивості
Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач.
Обладнання: моделі куба і тетраедра.
Хід уроку
І. Перевірка домашнього завдання
1. Колективне обговорення контрольних запитань № 9-11 та розв’язування задач № 23-25 (1).
2. Математичний диктант.
При паралельному перенесенні точка А переходить у точку В: варіант 1 – А (6; 7; 8), В (8; 2; 6); варіант 2 –
1) формули паралельного перенесення;
2) координати точки С, яка утворилася в результаті цього паралельного перенесення точки О (0; 0; 0);
3) координати точки D, яка утворилася в результаті цього паралельного перенесення точки С;
4) координати точки F, в яку перейшла точка M (1; 1; 1) в результаті цього паралельного перенесення;
5) формули паралельного перенесення, при якому точка В перейде в точку А.
Відповідь. Варіант 1. 1) х1 = х + 2, у1 = у – 5, z1 = z – 2; 2) С(2; -5; -2); 3) D(4; -10; -4); 4) F(-1; 6; 3); 5) x1 = х – 2, у1 = у + 5, z1 = z + 2.
Варіант 2.1) x1 = х – 1, y1 = y -1, z1 = z + 4 ; 2) C(-1; -1; 4); 3) D(-2; -2, -8); 4) F(2; 2; -3); 5) x1 = x + 1, y1 = y +
Перетворення фігури F в фігуру F1 називається перетворенням подібності, якщо будь-які довільні точки Х і Y фігури F переходять у точки X1, і Y1 фігури F1 такі, що Х1Y1 = k XY.
Перетворення подібності в просторі, як і на площині, переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими.
Дві фігури в просторі називаються подібними, якщо вони переводяться одна в одну перетворенням подібності.
Найпростішим перетворенням подібності в просторі є гомотетія.
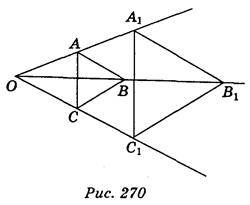
Гомотетія відносно центра О з коефіцієнтом k – це перетворення, яке переводить довільну точку Х у точку X1 променя ОХ таку, що ОХ1 = k OX. (рис. 270).
Далі формулюється теорема:
Перетворення гомотетії у просторі переводить довільну площину, яка не проходить через центр гомотетії, у паралельну площину (або в себе, коли k = 1).
Доведення проводиться так, як це зроблено в підручнику.
Розв’язування задач
1. Що являє собою фігура, подібна до куба з коефіцієнтом подібності: а) k = 2; б) k =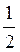 
; в) k = 1?
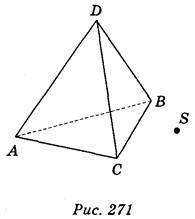
2. Побудуйте фігуру, гомотетичну даному тетраедру ABCD відносно точки S (рис. 271) з коефіцієнтом гомотетії: а) k = 2; б) k = 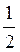; в) k = 1.
3. В яку фігуру переходить площина при гомотетії, якщо ця площина проходить через центр гомотетії?
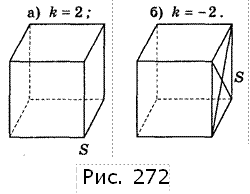
4. Побудуйте фігуру, в яку перейде куб при гомотетії відносно точки S (рис. 272) з коефіцієнтом гомотетії.
5. Трикутник АВС гомотетичний трикутнику А1В1С1 відносно початку координат з коефіцієнтом гомотетії k = 2. Знайдіть координати вершин трикутника А1В1С1, якщо А (1; 0; 0), В (0; 3; 0), С (0; 0; – 3).
6. Задача № 29 із підручника (с. 56).
III. Домашнє завдання
§4, п. 30; контрольні запитання № 12-13; задача № 28 (с. 56).
1) Що таке перетворення подібності? Перелічіть його властивості.
2) Яке перетворення називається гомотетією з центром О і коефіцієнтом А?
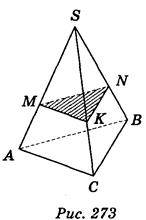
3) У трикутній піраміді SABC проведено переріз MNK так, що SM = 2MA, SK = 2KC, SN = 2NB (рис. 273). Укажіть, які з поданих тверджень правильні, а які – неправильні:
А) при гомотетії з центром S і коефіцієнтом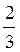 
точка М переходить у точку А;
Б) при гомотетії з центром S і коефіцієнтом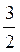 
площина АВС переходить у площину MNK;
В) AB = 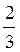MN;
Г) при гомотетії з центром S і коефіцієнтом – піраміда SABC переходить у піраміду SMNK.
4) У кубі ABCDA1B1C1D1 проведено перерізи BDC1 і MNK, де точки М, N, К – середини ребер СС1, ВС, DC (рис. 234). Укажіть, які з поданих тверджень правильні, а які – неправильні:
А) при гомотетії з центром С і коефіцієнтом 0,5 точка М переходить у точку C1;
Б) при гомотетії з центром С і коефіцієнтом 2 площина MNK переходить у площину BDC1;
В) BD = 2NK;
Г) площа перерізу BDC1 у 4 рази більша площі перерізу MNK.
(1 votes, average: 5.00 out of 5)
Loading...