ПЕРЕТВОРЕННЯ ВИРАЗІВ
РОЗДІЛ I ВИРАЗИ І ТОТОЖНОСТІ
&3. ПЕРЕТВОРЕННЯ ВИРАЗІВ
Ви вже знаєте, що два числові вирази МОЖУТЬ мати рівні значення, і тоді ці вирази можна прирівняти. Наприклад, 10 ∙ 2 + 5 = 31 – 2 ∙ 3. Про вирази зі змінними такого однозначно сказати не можна. Розглянемо приклади.
Задача 1. Чи можна прирівняти вирази: 1) 3а + b – а і 2 а + b; 2)abb : b і ab?
Розв’язання. 1. Вирази 3а + b – а і 2а + b містять однакові змінні і є цілими. Тому ОДЗ змінних першого виразу (ОДЗ-1) і другого виразу (ОДЗ-2) збігаються. Можемо записати спільно:
ОДЗ: а і b – будь-які
Оскільки За – а = 2а для будь-яких значень а, то, яким би не було b:
3а + b – а = 2а + b.
Отже, для будь-яких значень а і b вирази 3а + b – а і 2а + b прирівняти можна.
Наприклад:
Якщо а = -5, b = 0, то
3а + b – а = 3 ∙ (-5) + 0 – (-5) = -15 + 0 + 5 =-10,
2а + b = 2 ∙ (-5) + 0 = -10 + 0 = -10;
Якщо а = 1,5, b = 4,3, то
3а + b – а = 3 ∙ 1,5 + 4,3 – 1,5 = 4,5 + 4,3 – 1,5 = 7,3,
2а + b = 2 ∙ 1,5 + 4,3 = 3 + 4,3 = 7,3.
2. Вирази abb : b i ab містять однакові змінні. Але в першому виразі є ділення на вираз зі змінною, а другий вираз є цілим. Тому ОДЗ змінних першого виразу (ОДЗ-1) і другого виразу (ОДЗ-2) і не збігаються:
ОДЗ-1: а – будь-яке число, b ≠ 0,
ОДЗ-2: а і b –
Оскільки для b = 0 перший вираз втрачає зміст, то для будь-яких значень а і b вирази abb : b і ab прирівняти не можна. Рівність справджується лише для b ≠ 0.
Запам’ятайте!
Два вирази зі змінними називаються тотожно рівними, якщо вони набувають відповідно рівних значень за будь-яких значень їх змінних.
Зверніть увагу:
Перевіряючи два вирази зі змінними на тотожну рівність, спочатку потрібно впевнитися, що їх ОДЗ збігаються.
У розглянутій задачі 1 вирази 3а + b – а і 2а + b є тотожно рівними, а вирази abb : b і ab – ні.
Заміну виразу тотожно рівним йому виразом називають тотожним перетворенням виразу. Наприклад:
3a + b – а = 2а + b.
Тотожні перетворення використовують для спрощення виразів. Так, в останньому прикладі за допомогою тотожного перетворення вираз із трьома доданками замінили виразом із двома доданками. Для цього у виразі 3а + b – а спочатку виявили подібні доданки (3а і – а), а потім звели їх (тобто виконали вказану дію й отримали 2а).
Чому 3а і – а є подібними доданками? Тому що в цих доданків однакова буквена частина.
Спрощення виразів здійснюють згідно із законами додавання і множення. Пригадайте їх (табл. 3).
Таблиця З
Закони додавання і множення
ПЕРЕСТАВНИЙ ЗАКОН | СПОЛУЧНИЙ ЗАКОН | ||
Додавання | Множення | Додавання | Множення |
Для будь-яких а, b | Для будь-яких A, b, с | ||
A + b = b + a | A ∙ b = b ∙ a | (a + b) + c = a + (b + с) | (а ∙ b) ∙ с = а ∙ (b ∙ с) |
РОЗПОДІЛЬНИЙ ЗАКОН множення відносно додавання | |||
Для будь-яких а, b, с | |||
(a + b) ∙ с = a ∙ c + b ∙ с |
Задача 2. Спростіть вираз:
1)14а ∙ 0,5bс;
2) 25ху – 2х + 5у+ 3xy + 8x : 4 – 2.
Розв’язання.
1) 14а ∙ 0,5bс = 14 ∙ 0,5 abc = 7abc;
2) 25xy – 2х + 5y + 3хy + 8х : 4 – 2 =
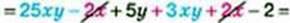
= 28ху – 0 ∙ х + 5y – 2 = 28ху + 5y – 2.
Зверніть увагу:
Подібні доданки, у яких числові коефіцієнти є протилежними числами, взаємно знищуються.
Так, у задачі 2 дістали: -2х + 2х = (-2 + 2) ∙ х = 0 ∙ х = 0. Щоб спростити вираз із дужками, спочатку розкривають дужки, спираючись на відповідні правила, а потім зводять подібні доданки.
Пригадаємо правила розкриття дужок.
Запамятайте!
Правила розкриття дужок.
Якщо перед дужками стоїть знак “+”, то, розкриваючи дужки, знаки доданків у дужках зберігають.
Якщо перед дужками стоїть знак “-“, то, розкриваючи дужки, знаки доданків у дужках змінюють на протилежні.
Наприклад:
-(х + 5) + (2х – 3) – (7 – 3х) = – x – 5 + 2x – 3 – 7 + 3x = 4x – 15.
Якщо перед дужками стоїть числовий множник або множник зі змінними, то, розкриваючи дужки, також користуються певними правилами.
Задача 3. Спростіть вираз 2х(у + 3z – 4) – 5(хy + хz -6).
Розв’язання. 2х(у + 3z – 4) – 5(хy + х2 – 6) = 2ху + 6хz – 8х – 5ху
5хz + 30 = – 3ху + хz – 8х + 30.
Зверніть увагу:
Щоб не помилитися, розкриваючи дужки у виразі:
1) порахуйте кількість доданків у дужках;
2) щоразу називайте кількість доданків у дужках і номер того доданка, який множите на вираз перед дужками, наприклад: “У дужках п’ять доданків; множимо перший доданок. У дужках п’ять доданків; множимо другий доданок і т. д.”.
Із курсу математики 5-6 класів ви знаєте, що перетворення суми або різниці виразів у добуток нерідко пов’язане
Із винесенням спільного множники за дужки.
Задача 4. У виразі 16nmk + 8nm – 12rnk винесіть спільний множник за дужки.
Розв’язання. Спочатку визначимо спільний множник для доданків даного виразу. Кожен доданок має числовий коефіцієнт, а НСД чисел 16, 8 і 12 дорівнює 4. Тому число 4 – це коефіцієнт спільного множника. Буквені частини кожного з доданків містять змінну m, а дві інші змінні (n і k) є не в кожному з доданків. Тому буквена частина спільного множника міститиме лише змінну т. Отже, спільний множник дорівнює 4m. Винесемо його за дужки:
16nmk + 8nm – 12mk = 4m(4nk + 2n – 3k).
Зверніть увагу:
Щоб перевірити, чи правильно виконали винесення спільного множника за дужки, виконайте обернену дію, тобто розкрийте дужки.
Дізнайтеся більше
Позначення невідомих величин за допомогою букв уперше зустрічається в записах у Діофанта Александрійського (бл. III ст.). Невідому величину Діофант називає “число” і позначає літерою ς1 квадрат невідомої – символом δv (скорочення від – “степінь”). Проте повне значення буквеної символіки відносять до заслуг Франсуа Вієта, який вперше застосував її для позначення величин і коефіцієнтів. Завдяки введенню буквених коефіцієнтів стало можливим застосування загальних формул та дослідження алгебраїчних рівнянь у загальному вигляді.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Які вирази називаються тотожно рівними?
2. Що називають тотожним перетворенням виразу?
3. Для чого використовують тотожні перетворення виразів?
4. Як зводять подібні доданки?
5. Як розкрити дужки, якщо перед дужками стоїть знак “+”; знак “-“?
6. Як винести спільний множник за дужки?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
86. Чи можуть бути тотожно рівними два вирази, якщо: 1) їх буквені частини містять неоднакові змінні; 2) їх буквені частини містять однакові змінні; 3) ОДЗ-1 і ОДЗ-2 не збігаються; 4) ОДЗ-1 і ОДЗ-2 збігаються; 5) вирази набувають нерівних значень за тих самих значень змінних; 6) один вираз є цілим, а другий містить ділення на змінну?
87. Чи правильно, що у виразі подібними є такі доданки, у яких:
1) той самий числовий коефіцієнт; 2) однакова буквена частина?
88. Чи правильно, що у виразі взаємно знищуються такі подібні доданки, у яких числові коефіцієнти є: 1) взаємно оберненими числами; 2) додатними числами; 3) від’ємними числами; 4) протилежними числами?
89. У виразі перед дужками стоїть знак “+”. Чи правильно розкриють дужки, якщо: 1) знак першого доданка збережуть, а знаки інших доданків поміняють; 2) знак першого й останнього доданків збережуть, а знаки інших доданків поміняють; 3) не поміняють знаки жодного з доданків?
90. У виразі перед дужками стоїть знак “-“. Чи правильно розкриють дужки, якщо: 1) знак першого доданка поміняють, а знаки інших доданків збережуть; 2) знак першого й останнього доданків поміняють, а знаки інших доданків збережуть; 3) поміняють знаки кожного з доданків?
91. У виразі перед дужками стоїть знак “-“. Скільки разів треба змінювати знаки доданків, якщо вираз у дужках містить: 1) два доданки; 2) три доданки; 3) п’ять доданків?
92. Чи є подібні доданки у виразі:
1) 5а + 3а;
2) а +2 b;
3) 7с + 4 – 5с + 9;
4) 6а +7b – 9с?
Назвіть їх.
93. У якому виразі взаємно знищуються доданки:
1) 4а + (-4а); 3)-4а – 4а; 5) 4а + 4а;
2) -4а + 4а; 4) 4а – 4а; 6) 4а – 4?
94. Зведіть подібні доданки у виразі:
1) 12а + 23а; 3)16n + 4n + 12; 5) 14p – 10p – 16p;
2) 46с – с; 4)12m + m + 4m; 6) 0,8k + 10,2k – 4,5.
95. Зведіть подібні доданки у виразі:
1) 16а – 9а;
2)3b + 12b – 16b;
3)15с – 12 + 5с;
4)15x – 8x – 12x.
96. Спростіть вираз:
1) 0,2а ∙ 6; 3)-3m – 4n; 5)-8а ∙ (-0,4bс);
2)7c ∙ 0,5d; 4) 10х ∙ (-1,1 уz); 6) 12t ∙ 5р ∙ (-4k).
97. Спростіть вираз:
1) а ∙ 14b; 3)-5m ∙ 1,4n;
2) 0,2с ∙ 8d; 4) -7ху ∙ (-0,5z).
98. Розкрийте дужки:
1) 2 ∙ (а – 4); 7)-х ∙ (5 – у);
2) 1,5 ∙ (b + 2); 8) (12а + 5) ∙ (- b);
3) -5 ∙ (6 – c); 9) -6х ∙ (у – 3);
4)-0,4 ∙ (d + 2); 10) (2n – m) ∙ (- 5p);
5) а ∙ (8 – 1,2b); 11) 3t ∙ (5p + k + 6);
6)(n – 0,5) ∙ m; 12) (2p-4k + 6t) ∙ 2а.
99. Розкрийте дужки:
1)7 (а – 2); 4) – n ∙ (0,5 – m);
2)-0,2 ∙ (b – 15); 5) 2х ∙ (-5 + у);
3) с ∙ (d – 10); 6) (3а – 2b + 1) ∙ (-с).
100. Розкрийте дужки і зведіть подібні доданки:
1) a – (a – b); 4) 2(k + p) – 2(k – р);
2) 4c + (5c – 4d); 5) -5(x – y + z) + 4(-x + y – z);
3) (n – m) – (m – n); 6) c – (b – a) + (a – b – c).
101 Розкрийте дужки і зведіть подібні доданки:
1)(c – d) – 2d; 3) 4(a – b) – 2(b – a);
2) 2х – (3у – 2х); 4) (n – 3m) – (4n – 6m).
102. Чи є тотожно рівними вирази:
1) 4а ∙ 8b і 32аb;
2) 4с + 2с + 6 і 6с + 6d;
3) 0,5 + 2n і 0,5 ∙ 4n;
4) 9m + 5 + m – 4m і 12m + 10 – 6m – 5;
5) 7ху : у і 7х;
6) 12cd : 2cd і 6cd : cd?
103. Чи є тотожно рівними вирази:
1 )5а + 6а i 11а; 3)5аb : а і 5b;
2) 12с – 2сd і 18cd; 4) (4n + 5n) : 3 і 3n?
104. Які з виразів є тотожно рівними:
1) 2а + 2b; 3)2(а + b);
2) а + b + а + 2; 4)2 а + b + b?
105. Винесiть спільний множник за дужки:
1) 11а + 11и; 7)-ах + 2bх;
2) 4c + 12d; 8) 10а – 5b – 15с;
3) 6nm – 21m; 9) -4х – 12y – 8z;
4) 18n – 24m; 10) ay + by – 8у;
5)2p + 12k – 8t; 11)-3n – 12m + 9p;
6)pk + 12k + 6tk; 12) 4а – 6b + 8с – 10
106. Винесіть спільний множник за дужки:
1) 6а – 6b; 3)3ху + 9х;
2)-5c – 20d; 4)-4n – 6nm + 2nр.
107. Спростіть вираз і знайдіть його значення:
1) (2х – 1) – (1 – 4х), якщо х = 0,25;
2) (2 – 5х) + (6,4х + 2,8), якщо х = -2,4;
3) (8,5 – 6,2х) – (4 – 7
– 7 ), якщо х = 11
), якщо х = 11 ;
;
4) 8х – (2  + 4,7х) – (4,7х – 6
+ 4,7х) – (4,7х – 6 ), якщо х = 5
), якщо х = 5 ;
;
108. Спростіть вираз і знайдіть його значення:
1) (5 – 14у) – (2,4 – 2,5у), якщо у = -4;
2) 5 – (2,4у + 3
– (2,4у + 3 ) + (2,5 – 1
) + (2,5 – 1 У), якщо у =
У), якщо у =  .
.
109. Замініть вираз на тотожно рівний:
1) 5а + 16а – 7b + 12b;
2) 25с -31d – 23d + 12с;
3) 0,6m + 3,4n – 7,2 n – 6,8m;
4) 7у – 3,5х – 4,5х + 13у;
5)  Р – 1
Р – 1 K –
K –  р + k;
р + k;
6)12,5t – 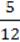 + 5,5 –
+ 5,5 – 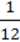 .
.
110. Замініть вираз на тотожно рівний:
1) 12с +14d – 4c -23d;
2) -5,6n + 3,4m + 4,5m – 7,2n;
3)  X – 4,5 + 2,5х + 5
X – 4,5 + 2,5х + 5 У;
У;
4) 2,8 k + 1,4 – 7k + 4  K.
K.
111. Розкрийте дужки і зведіть подібні доданки:
1) -3(m – 0,2n) +  (10n – 1,5m);
(10n – 1,5m);
2) 0,3(n – 5m) – 1,2(-n – 1,25m);
3) (4 n – 0,8m)
n – 0,8m)  5 – 0,6 (
5 – 0,6 ( N – 3,5m) + 4,5m;
N – 3,5m) + 4,5m;
4) -2,6(4m – 5n) + (10n – 5m) ∙ (-1,3) – (4,8n + 1,3m) ∙ 5.
112. Розкрийте дужки і зведіть подібні доданки:
1) 6,4(2с – 0,5d) – 0,4(16с – 8d);
2) 0,9 (3 D + 1
D + 1  C) – (5,2c – d) ∙
C) – (5,2c – d) ∙ 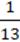 + 2,7 c.
+ 2,7 c.
113. Винесіть спільний множник за дужки:
1) 6ab – 4ac + 12ad;
2) -24mn + 1,6mp – 8mk;
3)  Abc –
Abc –  Acd + 3
Acd + 3 akc – 4 apc;
akc – 4 apc;
4) -2,5xy + 1,5xyz – 5xyn + 3,5.
114. Винесіть спільний множник за дужки:
1) 4,9xy – 1,4xz + 7yz;
2)  Abc –
Abc – 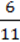 Abc + 1
Abc + 1 Abcd – 9.
Abcd – 9.
115. Спростіть вираз і знайдіть його значення:
1) (5,4xy – 6,8xz + 4) – (3,2xy – 4,8xz + 5,8) – 2,2, якщо х = 1,5; у = -4; z = -0,2;
2) – 20 (0,2xy – 0,3x –  Y) + (ху – 3у – 2х) ∙ 3, якщо х = -0,6; у = 0,4;
Y) + (ху – 3у – 2х) ∙ 3, якщо х = -0,6; у = 0,4;
3) (2xy – 5xz) ∙ 0,4 – (xy + 3yz) . 0,8 + (5xz – 2yz) ∙ (-0,2), якщо х =3 ; y = 1
; y = 1 ; z = -12,6;
; z = -12,6;
4) (x – y) ∙ z – (4х – z) ∙ у + (5у – 7z) x, якщо x = -2,4; y = 1,5; z = 1 .
.
116. Спростіть вираз і знайдіть його значення:
1) -4(0,5х + у) + 0,8(3x – 2z) – 6(0,4z – 0,1y), якщо х = -5;у = 10; z = 5 ;
;
2) (5x + 6y) ∙ 0,52 + (3x -2z) – 1,5y – (2,52 – y) ∙ x, якщо х = 5,2; у = 0,1;
117. Знайдіть значення виразу:
1) 4а + 12b, якщо а + 3b = 28;
2) 7хz – 14yz, якщо х – 2у = 17; z = 0,4;
3) 6ab – 8aс, якщо а = -0,12; 3b – 4с = 5;
4) 3ху – 0,6х + 0,9у, якщо х – 5ху – 1,5y =1,25.
118. Знайдіть значення виразу:
1) 15с – 3y, якщо 5с – d = -3;
2)-12mn + 18mр, якщо m =0,5; 2n – 3p = -8.
119. Складіть та спростіть вираз: 1) до добутку чисел а і b додати третю частину різниці чисел а і b; 2) потроєну суму чисел а і b поділити на половину їх різниці. Знайдіть значення виразу, якщо а = 5, b = -0,4
120. Складіть та спростіть вираз: потроєну різницю чисел с і d поділити на подвоєну їх суму. Знайдіть значення виразу, якщо с =-2, d =1,2.
121. Що потрібно вставити замість зірочок, щоб отримати тотожно рівні вирази?
1) 4а(* + 4,5с) = 10аb + *;
2) * ( X – 1
X – 1 Y) = -4x + 7y;
Y) = -4x + 7y;
3) 3,6ac – * = 6c(* – 3dc);
4) * + 5 Yz =
Yz =  Y(1,5xy + *).
Y(1,5xy + *).
122. Складіть вираз для знаходження суми: 1) чотирьох послідовних натуральних чисел; 2) п’яти послідовних непарних натуральних чисел; 3) шести послідовних парних натуральних чисел; 4) трьох натуральних чисел, кратних 6.
123. Відомо, що  = 12 Знайдіть значення виразів: b
= 12 Знайдіть значення виразів: b
1) 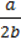 ;
;
2) 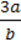 ;
;
3) 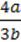 .
.
124. Знайдіть значення х, якщо:
1) х – у = 5,  = -3;
= -3;
2) х + 3у = 4, 2х + 3у=8.
125. Доведіть, що при виконанні рівності  =
=  , b ≠ 0,d ≠ 0, виконується така рівність:
, b ≠ 0,d ≠ 0, виконується така рівність:
1) 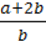 =
= 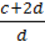 ;
;
2) 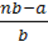 =
= 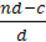 ;
;
3) 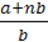 =
= 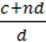 ;
;
4) 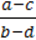 =
=  ;
;
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
126. Купили 3 кг яблук, 2 кг груш і 4 кг слив. Складіть вираз для обчислення вартості фруктів, якщо ціна 1 кг: яблук – а грн, груш – b грн, слив – с грн.
127. Складіть вираз щодо витрат часу Тетянкою на виконання домашнього завдання, якщо: 1) на англійську мову витрачено а хв; 2) на математику – у 1,5 рази більше, ніж на виконання англійської мови; 3) на українську літературу – на 10 хв, більше, ніж на виконання математики. Скільки часу виконувала домашнє завдання Тетянка, якщо завдання з англійської мови вона виконала за 20 хв?
128. Складіть задачу, подібну до попередньої, за вашими власними витратами часу на виконання домашнього завдання.
ЗАДАЧІ НА ПОВТОРЕННЯ
129. Знайдіть середнє арифметичне трьох послідовних натуральних чисел, менше з яких є найбільшим трицифровим числом.
130. Середнє арифметичне трьох чисел дорівнює 18. Знайдіть ці числа, якщо перше з них у 2 рази, а друге – у 1,5 раза більше за третє.
131. Розв’яжіть рівняння:
1)  =
= 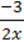 ;
;
2)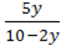 =
= 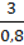 .
.