Періодичність тригонометричних функцій
УРОК 8
Тема. Періодичність тригонометричних функцій
Мета уроку: Введення поняття періодичної функції; знаходження найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій
У = sin (kx + b), у = cos (kx + b),
У = tg (kx + b), у = ctg (kx + b).
І. Перевірка домашнього завдання
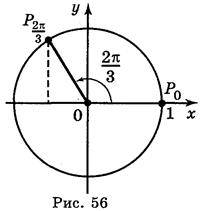
1. Побудуйте на одиничному колі точку Р?, на яку відображаються початкова точка Р0 (1; 0) при повороті на? рад навколо центра, якщо:
І в. | ІІ в. |
|
|
2. Знайдіть
| 2. Знайдіть
|
3. Визначте знак добутку Sin 1 ? cos 2 ? tg 3. (5 бали) | 3. Визначте знак добутку Сos 1 ? sin 2 ? ctg 3. (5 бали) |
Відповідь:
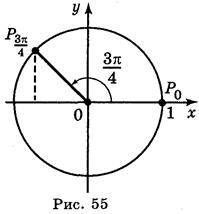
І в.: 1. Рис. 55. 2. 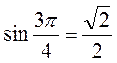 ,
, 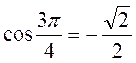 ,
, 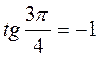 ,
, 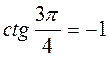
ІІ в.: 1. Рис. 56. 2. 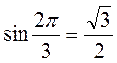 ,
, 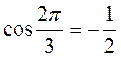 ,
, 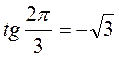 ,
, 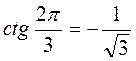 .3.мінус.
.3.мінус.
II. Формування поняття періодичної функції, періодe функції
У природі часто зустрічаються явища, які повторюються періодично. Наприклад, Земля при обертанні навколо Сонця періодично повертається У своє початкове положення через рік, два роки, три роки і т. д., тому говорять, що період обертання Земля навколо Сонця дорівнює одному року. Періодичний характер мають рухи маховика і колінчатого вала. Властивість періодичності мають звукові, електромагнітні явища, робота серця людина і т. д. Закономірності періодичних явищ описуються періодичними функціями, до вивчення яких ми і приступаємо.
Функція у = f(x) називається періодичною з періодом Т 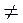 0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) = f(x – Т) = f(x).
0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f(x + Т) = f(x – Т) = f(x).
Так як одній і тій самій точці Р? одиночного кола відповідає нескінченна множина дійсних чисел? + 2?k, де k  Z, то
Z, то
Sin(? + 2nk) = sin?
Cos(? + 2nk) = cos?
Звідси випливає, що 2nk – періоди функції синус і косинус (k 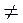 0).
0).
Доведемо, що число 2? є найменшим додатним періодом функції у = cos х. Нехай? > 0 – період косинуса, тобто для будь-якого х виконується нерівність cos (х + ?) = cos x. Взявши х = 0, одержимо cos Т = 1. Звідси? = 2nk, k  ?. Через те що? > 0, ? може дорівнювати 2?, 4?, 6?… і тому період не може бути меншим 2?.
?. Через те що? > 0, ? може дорівнювати 2?, 4?, 6?… і тому період не може бути меншим 2?.
Можна довести, що найменший період функції у = sin x теж дорівнює 2?. Нехай? – довільний період синуса. Тоді sin(x + ?) = sin x для будь-якого х. Взявши х =  , одержимо sin
, одержимо sin 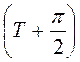 = sin
= sin  = 1, але sin
= 1, але sin 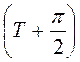 = 1, якщо Т +
= 1, якщо Т +  =
=  + 2?n, n
+ 2?n, n  ?, тому? = 2?n. Найменше додатне число виду 2?n, n
?, тому? = 2?n. Найменше додатне число виду 2?n, n ? є число 2?.
? є число 2?.
Доведемо, що найменшим додатним періодом функції у = tg х є число?. Нехай Т – додатний період тангенса, тобто tg(x+ Т) = tg х. Взявши х = 0, маємо tg Т = tg 0 = 0. Звідси Т = ?n, n  ?. Через те що найменше ціле додатне n = 1, ? – найменший період функції у = tg х. Найменшим додатним періодом котангенса теж є число?. Отже, tg (? + ?n) = tg?, ctg (? + ?n) = ctg?.
?. Через те що найменше ціле додатне n = 1, ? – найменший період функції у = tg х. Найменшим додатним періодом котангенса теж є число?. Отже, tg (? + ?n) = tg?, ctg (? + ?n) = ctg?.
Як правило, слова “найменший додатний період” опускають. Прийнято говорити, що період тангенса і котангенса дорівнює?, а період косинуса і синуса дорівнює 2?.
Справедливе твердження.
Якщо функція у = f(x) періодична і має період Т, то функція у = Af(kx + b), де А, k, b – постійні (k 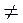 0), також періодична, причому її період дорівнює
0), також періодична, причому її період дорівнює 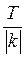 .
.
Доведемо це твердження.
Спочатку доведемо, що T0 = 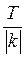 є періодом функції у = Af(kx + b):
є періодом функції у = Af(kx + b):
Af(k(x + T0) + b) = Af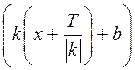 = Af(kx ± T + b) = Af(kx + b ± T) = Af(kx + b).
= Af(kx ± T + b) = Af(kx + b ± T) = Af(kx + b).
Нехай T0 – період функції у == Af(kx + b), тобто
Af(k(x + T0) + b)= Af(kx + b),
Af(kx +b+ kT0) = Af(kx +b).
Позначивши kx + b = x1, маємо Af(x + kT0) = Af(x1).
Через те що найменшим періодом функції f(x) є Т, то ¦k¦T0 = ?, звідси Т0 = 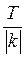 .
.
III. Усвідомлення поняття періодичної функції
1. Обчисліть: a) sin 1470°; б) tg 1860°; в) cos 1140°; г) ctg 1125°.
Відповідь: а)  ; б)
; б)  ; в)
; в)  ; г) 1.
; г) 1.
2. Знайдіть значення: a) sin 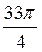 ; б) cos
; б) cos 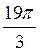 ; в) tg
; в) tg 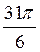 ; г) ctg
; г) ctg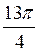 .
.
Відповідь: а) 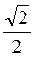 ; б)
; б)  ; в)
; в) 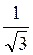 ; г) 1.
; г) 1.
3. Знайдіть найменший додатний період функцій:
А) у =  Sin2х; б) у = 3cos 4x; в) y = 5tg
Sin2х; б) у = 3cos 4x; в) y = 5tg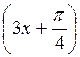 ; г) y=0,6ctg
; г) y=0,6ctg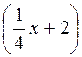 .
.
Відповідь: а) ?; б)  ; в)
; в)  ; г) 4?.
; г) 4?.
4. Знайдіть значення sin?, якщо:
A) sin (? + 2?) = 0,3;
Б) sin (4? – ?) = 0,2;
В) sin (? + 6?) = 0,5;
Г) sin (? – 2?) = 0,1.
Відповідь: а) 0,3; б) -0,2; в) 0,5; г) 0,1.
IV. Підсумок уроку
V. Домашнє завдання
Розділ І § 5. Запитання і завдання для повторення до розділу І № 47-49. Вправа № 24 (1-3). Повторіть геометричні перетворення графіків функцій (таблиця 1 підручника).
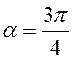 . (3
. (3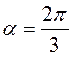 . (3 бали)
. (3 бали)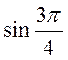 ,
, 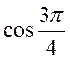 ,
, 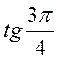 ,
, 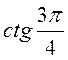 . (4 бали)
. (4 бали)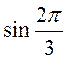 ,
, 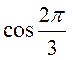 ,
, 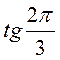 ,
,