Головна ⇒ 📌Довідник з геометрії ⇒ Площа трикутника
Площа трикутника
Геометрія
Площі фігур
Площа трикутника
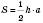 , де h – висота, a – сторона, до якої проведена ця висота.
, де h – висота, a – сторона, до якої проведена ця висота.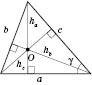
Оскільки 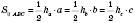 , то
, то 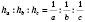 .
.
Висоти трикутника обернено пропорційні сторонам, на які вони опущені.
Зверніть увагу: більшій стороні трикутника відповідає менша висота, і навпаки.
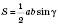 ,
, 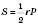 , де P – периметр трикутника, r – радіус вписаного кола.
, де P – периметр трикутника, r – радіус вписаного кола.
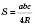
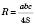 , де R – радіус описаного кола.
, де R – радіус описаного кола.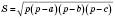 – Формула Герона.
– Формула Герона.p – півпериметр трикутника.
Площа прямокутного трикутника
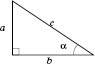
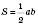
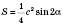
Площа рівностороннього трикутника
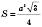 .
.
Властивості медіани трикутника
Медіана ділить трикутник на два рівновеликі (тобто такі, що мають однакову площу) трикутники.
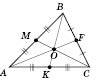
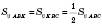 .
.
Три медіани трикутника розбивають його на шість рівновеликих трикутників.
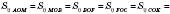
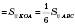 .
.
Related posts:
- Площа трикутника Урок № 47 Тема. Площа трикутника Мета: домогтися засвоєння учнями змісту та ідеї доведення теореми про формулу плоті трикутника й наслідків з неї. Сформувати вміння: – відтворювати зміст вивчених формул; – записувати формули відповідно до заданих позначень елементів трикутників; – застосовувати вивчені формули до розв’язування задач. Тип уроку, засвоєння вмінь та навичок. Наочність та обладнання: […]...
- Ознаки рівнобедреного трикутника Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівнобедреного трикутника Теорема 1. Якщо в трикутнику два кути рівні, то він рівнобедрений. Теорема 2. Трикутник рівнобедрений, якщо: – одна з його висот є медіаною; – одна з його медіан є бісектрисою; – одна з його висот є бісектрисою. Теорема 3. Трикутник рівнобедрений, якщо: – дві його висоти […]...
- Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...
- Середня лінія трикутника Геометрія Трикутники Середня лінія трикутника Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. Теорема 1. Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні й дорівнює її половині. На рисунку праворуч: ;. У трикутнику можна провести три середні лінії. Вони утворюють трикутник з такими ж кутами, як даний, і […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...
- Медіана, бісектриса і висота трикутника Урок № 24 Тема. Медіана, бісектриса і висота трикутника Мета: домогтися засвоєння учнями: – змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”; – уявлення про положення висот у різних видах трикутника. Сформувати вміння: – зображати медіани, висоти та бісектриси трикутника; – розрізняти ці відрізки, виходячи з умови задачі. Тип уроку: застосування знань, умінь та навичок. […]...
- Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...
- Площа прямокутника Геометрія Площі фігур Площа прямокутника ; ; d = AC; , де R – радіус описаного кола, R = AO....
- Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...
- Трикутник загального виду – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник загального виду R – радіус описаного кола R – радіус вписаного кола Формула Герона:...
- Площа ромба Геометрія Площі фігур Площа ромба , . У ромбі висоти дорівнюють одна одній. ; d1 = AC, d2 = = BD; , де r – радіус вписаного в ромб кола....
- Знаходження площі трикутника за радіусом вписаного та описаного кіл УРОК № 14 Тема. Знаходження площі трикутника за радіусом вписаного та описаного кіл Мета уроку: виведення формул для знаходження площі трикутника за радіусом вписаного та описаного кіл. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Площі трикутників і чотирикутників” [13], посібник [14]. Вимоги до рівня підготовки учнів: […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Площа паралелограма Геометрія Площі фігур Площа паралелограма Площа паралелограма обчислюється за формулою S = ha, де h – висота, a – сторона, до якої проведена ця висота. Оскільки (див. рисунок), то . Із двох різних висот паралелограма більша та, яка опущена на меншу сторону. AC = d1; BD = d2; ; . Трикутники AOB, BOC, COD, DOA […]...
- Застосування подібності: властивість бісектриси трикутника Урок № 37 Тема. Застосування подібності: властивість бісектриси трикутника Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Формувати вміння: – відтворювати зміст вивченої теореми; – за готовими рисунками із зображенням трикутника та його бісектриси знаходити пропорційні відрізки; – виконувати записи відповідно до формулювання теореми та умови задачі; – застосовувати […]...
- Знаходження площі трикутника за двома сторонами і кутом між ними УРОК № 12 Тема. Знаходження площі трикутника за двома сторонами і кутом між ними Мета уроку: виведення формули для знаходження площі трикутника за двома сторонами і кутом між ними. Формування вмінь застосовувати виведену формулу до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Площа трапеції Геометрія Площі фігур Площа трапеції Де h – висота, a, b – основи трапеції. , де h – висота, m – середня лінія. . Якщо в трапецію можна вписати коло радіуса r, то , де P – периметр трапеції. Деякі властивості трапеції . ; . Якщо ; ....
- Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...
- СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...