Площа трикутника
Урок № 47
Тема. Площа трикутника
Мета: домогтися засвоєння учнями змісту та ідеї доведення теореми про формулу плоті трикутника й наслідків з неї. Сформувати вміння:
– відтворювати зміст вивчених формул;
– записувати формули відповідно до заданих позначень елементів трикутників;
– застосовувати вивчені формули до розв’язування задач.
Тип уроку, засвоєння вмінь та навичок.
Наочність та обладнання: конспект “Площа трикутника. Площа трапеції”.
Хід уроку
I. Організаційний етап
II. Перевірка
Учитель збирає зошити учнів із виконаною домашньою самостійною роботою (див. вище). Учням оголошується правильне розв’язання за рисунками, зображеними на дошці заздалегідь.
ІІІ. Формулювання мети і завдань уроку
Для створення ситуації, що допоможе учням зрозуміти ідею доведення теореми про площу трикутника, пропонуємо учням задачу.
Задача. На дошці зображено дві фігури: паралелограм ABCD і трикутник MNK такі, що AD = МК, і висоти проведені до цих сторін (ВН, NF), також рівні (див. рис).
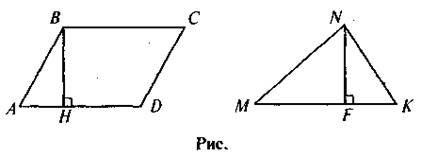
Площа паралелограма відома. Як знайти площу трикутника?
Пошук відповіді
– по-перше, існування протиріччя між набутими знаннями та змістом задачі (учні вміють знаходити площі прямокутника і паралелограма, а за змістом задачі слід знайти площу трикутника);
– по-друге, зміст задачі містить “підказку” – обчислення площі трикутника слід якось пов’язати з обчисленням площі паралелограма.
Отже, мета уроку – подолання протиріччя, тобто вивчення формули для обчислення плоті трикутника; засобом виведення шуканої формули є формула площі паралелограма.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту та доведення теореми про формулу площі трикутника, а також наслідків з неї, учням слід активізувати знання і вміння щодо властивості діагоналі паралелограма і діагоналей ромба, властивості площ рівних фігур, аксіом площ, означення прямокутного трикутника, означення рівностороннього трикутника та формули обчислення висоти рівностороннього трикутника через його сторону.
1. Яка з фігур на рис. 1 зайва? Чому?
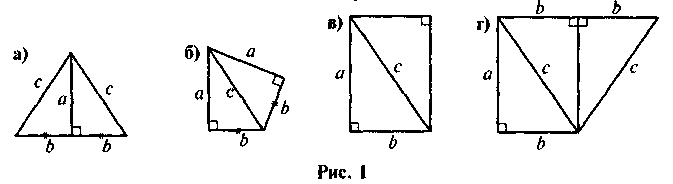
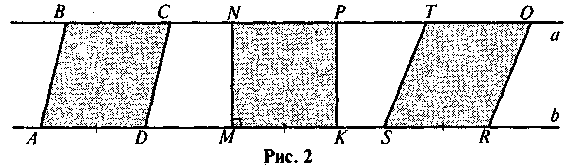
2. Прямі а і b паралельні. Площа паралелограма ABCD дорівнює S. Чому дорівнюють площі інших фігур на рис. 2 (AD = МК = SR)?
3. У трикутнику ABC АВ = ВС = а,  А = 60°. Чому дорівнює ВН і АР (ВН
А = 60°. Чому дорівнює ВН і АР (ВН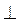 АС, АР
АС, АР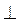 ВС)? Знайдіть довжини цих відрізків, якщо АВ = 3 см, PC = 2 см, AC = 4
ВС)? Знайдіть довжини цих відрізків, якщо АВ = 3 см, PC = 2 см, AC = 4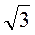 см (рис. 3).
см (рис. 3).
4. У паралелограмі ABCD AB = 7, BD = 6, PA0B = 18 (рис. 4). Знайдіть AC.
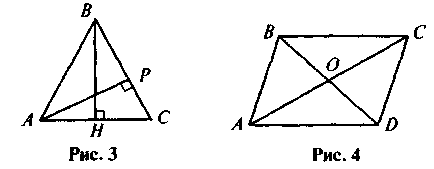
5. Знайдіть кути ромба ABCD, якщо відомо, що:
A)  ABD = 53° ; б)
ABD = 53° ; б)  CDE = 32°; в) ВК
CDE = 32°; в) ВК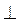 AD,
AD,  KBD = 20°.
KBD = 20°.
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема (формула площі трикутника).
2. Площа прямокутного трикутника.
3. Площа ромба.
4. Площа рівностороннього трикутника.
5. Властивість медіани трикутника.
@ Викладення формулювання і способу доведення теореми, що виражає формулу обчислення площі трикутника, є класичним. Тому вивчення цієї частини матеріалу уроку можна провести традиційно: учням пропонується самостійно розглянути відповідний пункт підручника та вивчити зміст і скласти план доведення теореми. Після виконання цієї роботи незрозумілі моменти доведення коментуються вчителем, зміст закріплюється на такому завданні.
За рис. 5 доповнити записи, щоб вони стали правильними рівностями.
S – площа? MNK;
S = … MK – NR;
S = 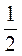 MN – …
MN – …
S = …MF…
… = MN – SK.
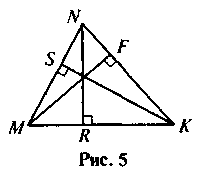
Вивчення наслідків з доведеної формули для площі трикутника можна провести, заохочуючи учнів до досліджень запитаннями:
– Чи існує трикутник, сторона якого є висотою? Як записати доведену формулу для площі такого трикутника?
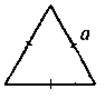
– Чи існує трикутник, всі висоти якого рівні? Як виражається висота цього трикутника через його сторону? Як записати формулу площі для такого трикутника?
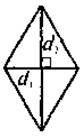
– На які фігури розбивається ромб всіма своїми діагоналями? Що ви знаєте про ці фігури? Як виражається площа ромба через площу цих трикутників?
Закінчивши обговорення питань, учні виконують відповідні записи в зошитах. (Щоб учні усвідомили логічні зв’язки між вивченими на уроці формулами, записи цих формул можна записати у вигляді схеми, рис. 6.)
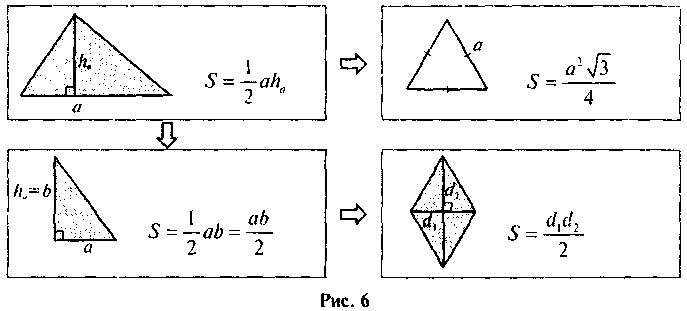
Конспект 19 | |||||
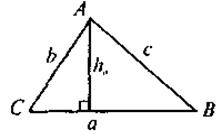
Площа трикутника. Площа трапеції Якщо в? ABC: ha – висота, проведена до сторони a, то SАВС = Наслідки |
| ||||
1) Якщо в? ABC | 2) Якщо d1 і d2 діагоналі ромба, то | 3) Якщо трикутник рівносторонній зі стороною a, то | |||
|
|
|
|
|
|
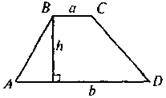
Якщо в трапеції ABCD (BC || AD) BC = a, AD = b, H – висота, то |
|
VI. Формування первинних умінь
Виконання усних вправ
1. Площа трикутника ABC дорівнює S. Чому дорівнює площа паралелограма ABCD, три вершини якого збігаються з вершинами даного трикутника?
2. За якою формулою доцільно обчислювати площу прямокутного трикутника, якщо відомі:
А) довжини гіпотенузи і проведеної до неї висоти;
Б) довжини двох катетів?
3. Два рівновеликі трикутники мають рівні висоти. Чи означає це, що основи даних трикутників також рівні?
4. Доведіть, що більшій стороні трикутника завжди відповідає менша висота.
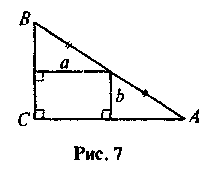
5. Яка площа трикутника ABC на рис. 7?
6. У паралелограмі провели діагоналі. Чи рівні площі всіх утворених чотирьох трикутників?
Виконання письмових вправ
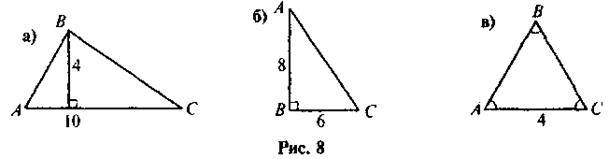
1. За даними рисунка 8 знайдіть площу трикутника ABC.
2. Знайдіть площу:
А) рівнобедреного трикутника з основою 10 см і бічною стороною 13 см;
Б) трикутника ABC, в якому АВ = 17 см, а висота ВН ділить сторону АС на відрізки АН = 8 см і НС = 2 см.
3. Площа трикутника дорівнює 72 см2. Знайдіть периметр трикутника, якщо його висоти дорівнюють 9 см, 12 см і 24 см.
4. Знайдіть площу ромба, діагоналі якого дорівнюють 8 м і 20 м.
5. Знайдіть площу:
А) трикутника ABC з висотою ВН, якщо АВ= 13 см, ВС = 15 см, ВН = 12 см, а точка Н лежить на відрізку АС;
Б) прямокутного трикутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см;
В) рівностороннього трикутника з висотою 2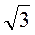 см.
см.
6. На рисунку 9 подано одиничний квадрат. Знайдіть площу заштрихованої фігури.
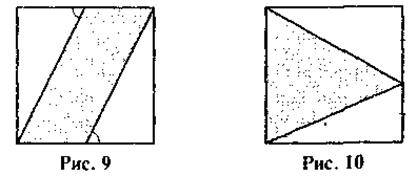
7. На рисунку 10 подано одиничний квадрат. Знайдіть площу заштрихованої фігури.
VII. Підсумки уроку
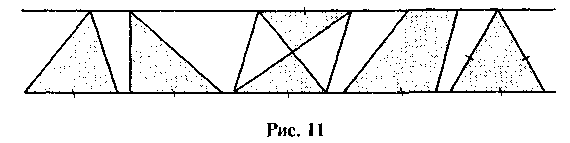
Яка із фігур на рисунку 11 зайва? Чому?
VIIІ. Домашнє завдання
Вивчити зміст теореми, її доведення та наслідки.
Розв’язати задачі.
1. Знайдіть площу:
А) прямокутного трикутника з гіпотенузою 20 см і катетом 12 см;
Б) гострокутного трикутника ABC з висотою AN = 4 см, якщо ВН = 2 см.  C = 45°.
C = 45°.
2. Знайдіть гіпотенузу прямокутного трикутника, якщо його площа дорівнює 20 см2. а висота, проведена з вершини прямого кута, – 4 см.
3. Знайдіть діагоналі ромба, якщо одна з них удвічі більша за другу, а площа ромба дорівнює 64 см2.
4. Знайдіть площу рівнобедреного трикутника з периметром 16 см і висотою завдовжки 4 см. проведеною до основи.
5. Накресліть гострокутний трикутник і проведіть у ньому висоту. Проведіть необхідні вимірювання та обчисліть:
А) площу даного трикутника;
Б) площі трикутників, на які даний трикутник ділиться висотою.
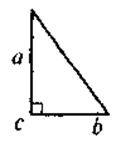
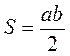
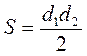
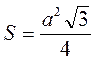
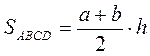 або S = MN – h ( MN – середня лінія)
або S = MN – h ( MN – середня лінія)