Подібність фігур
Геометрія
Подібність фігур
Перетворення фігури F у фігуру 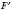 називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів.
називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одну й ту саму кількість разів.
Якщо відстані змінюються у k разів, то k називається Коефіцієнтом подібності. Якщо 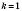 , перетворення подібності є рухом.
, перетворення подібності є рухом.
Нехай F – дана фігура й О – фіксована точка.
Через довільну точку Х фігури F проведемо промінь ОХ і відкладемо на ньому відрізок 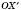 , що дорівнює
, що дорівнює 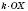 , де k – додатне число. Перетворення фігури F, при якому кожна її точка Х переходить у точку
, де k – додатне число. Перетворення фігури F, при якому кожна її точка Х переходить у точку 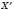 , побудовану в такий спосіб, називається Гомотетією відносно центраО з коефіцієнтом k. Якщо k – число від’ємне, відрізок
, побудовану в такий спосіб, називається Гомотетією відносно центраО з коефіцієнтом k. Якщо k – число від’ємне, відрізок 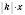 відкладають на півпрямій, що є доповняльною до ОХ.
відкладають на півпрямій, що є доповняльною до ОХ.
На рисунку наведена гомотетія відносно центра з коефіцієнтом 2.
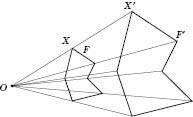
Теорема. Гомотетія є перетворенням подібності.
Related posts:
- Подібність просторових фігур – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Подібність просторових фігур Перетворення фігури F називається Перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюють себе в одну й ту саму кількість разів. Як і на площині, перетворення подібності в просторі переводить прямі у прямі, півпрямі у півпрямі, відрізки у відрізки і зберігає кути між півпрямими. […]...
- Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...
- Подібність фігур. Площі подібних фігур УРОК № 39 Тема. Подібність фігур. Площі подібних фігур Мета уроку: формування поняття подібності фігур; вивчення теореми про площі подібних фігур; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують подібність фігур; наводять приклади подібних фігур; формулюють теорему […]...
- Перетворення подібності та його властивості Урок 50 Тема. Перетворення подібності та його властивості Мета уроку: формування знань учнів про подібність просторових фігур, вивчення властивостей перетворення подібності та застосування їх до розв’язування задач. Обладнання: моделі куба і тетраедра. Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення контрольних запитань № 9-11 та розв’язування задач № 23-25 (1). 2. Математичний диктант. При […]...
- Симетрія відносно прямої Геометрія Рух Симетрія відносно прямої Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок . Точка називається Симетричною точці X відносно прямої А. Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а. Очевидно, […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...
- Поняття про рух, рівність фігур у просторі Урок 48 Тема. Поняття про рух, рівність фігур у просторі Мета уроку: формування понять: рух, рівні фігури. Доведення нової властивості руху: площина під час руху переходить у площину. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 48), модель куба. Хід уроку 1. Відповісти на запитання учнів, які виникли […]...
- Властивості перетворення подібності Геометрія Подібність фігур Властивості перетворення подібності Теорема 1. Перетворення подібності переводить прямі у прямі, півпрямі – у півпрямі, відрізки – у відрізки. Теорема 2. Перетворення подібності зберігає кути між півпрямими. Із цього випливає, що перетворення подібності переводить паралельні прямі в паралельні прямі. Дві фігури називаються Подібними, якщо вони переводяться одна в одну перетворенням подібності. Позначення: […]...
- Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...
- Гомотетія і перетворення подібності 480. ΔABC і ΔA1B1С1 гомотетичні з центром Р, R = 2. 481. Тетраедр DA1B1С1 гомотетичний тетраедру DABC відносно т. D, R = 0,5. 482. Р і A симетричні відносно В. Тетраедр A1B1C1D1 гомотетичний тетраедру ABCD відносно т. Р із коефіцієнтом R = -1. 483. В результаті гомотетії відносно т. А т. О – центроїд грані […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Симетрія відносно прямої УРОК № 35 Тема. Симетрія відносно прямої Мета уроку: формування поняття симетрії відносно прямої; вивчення властивостей симетрії відносно прямої; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно прямої; будує фігури, у які переходять дані […]...
- Зображення просторових фігур на площині Геометрія Стереометрія Зображення просторових фігур на площині Для зображення просторових фігур на площині, як правило, користуються Паралельним проектуванням. Беремо довільну пряму h, яка перетинає площину рисунка , проводимо через довільну точку A фігури пряму, паралельну h. Точка перетину цієї прямої з площиною рисунка буде зображенням точки A. Побудувавши таким чином зображення кожної точки фігури, дістанемо […]...
- Паралельне проектування та його властивості. Зображення просторових фігур на площині Урок 21 Тема. Паралельне проектування та його властивості. Зображення просторових фігур на площині Мета уроку: формування знань про паралельне проектування. Вивчення властивостей паралельного проектування. Дати уявлення про зображення просторових фігур на площині. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Відповісти на запитання, які виникли в учнів при розв’язуванні домашньої задачі. 2. Самостійна […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Площі фігур Геометрія Площі фігур Геометричну фігуру називають Простою, якщо її можна розбити на скінченну кількість плоских трикутників. Для простих фігур Площа – це додатна величина, числове значення якої має такі властивості: – рівні фігури мають рівні площі; – якщо фігура розбивається на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площі її частин; […]...
- Перетворення простору 1. 1) Вектор паралельного перенесення, що переводить відрізок ОА в СВ: Вектор, що переводить відрізок ОС в АВ: 2) Вектор, що переводить ОС в АВ: Вектор, що переводить О А в СВ: 3) Вектор, що переводить ОС в АВ: Вектор, що переводить ОА в СВ: 4) Вектор, що переводить ОС в АВ: Вектор, що переводить […]...
- Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
- Композиції рухів і рівність фігур 446. Образом відрізка АВ в результаті композиції центральної симетрії відносно т. О і повороту на кут 90° є відрізок А2В2. 447. Образом даного паралелепіпеда в результаті композиції паралельного перенесення не вектор та симетрії відносно площини а є паралелепіпед A′′B′′C′′D′′A′′1B’′1C′′1D”1. 448. А) А1 симетрична А(1; -2; 5) відносно М. x1 =-1 y1 = 2 z1 = […]...
- Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...
- Подібність трикутників за двома сторонами та кутом між ними Урок № 29 Тема. Подібність трикутників за двома сторонами та кутом між ними Мета: домогтися розуміння учнями змісту другої ознаки подібності трикутників та плану її доведення. Формувати вміння: – відтворювати зміст вивченої ознаки; – виділяти в трикутниках елементи для визначення їх подібності за двома сторонами та кутом між ними; – застосовувати формулювання другої ознаки подібності […]...
- Поворот УРОК № 36 Тема. Поворот Мета уроку: формування поняття повороту та вивчення властивостей повороту; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують поворот; будує фігури, у які переходять дані фігури при повороті; застосовують вивчені означення і […]...
- Подібність трикутників за трьома сторонами Урок № 30 Тема. Подібність трикутників за трьома сторонами Мета: домогтися розуміння учнями змісту ознаки подібності трикутників за трьома сторонами, плану їх доведення. Формувати вміння: – відтворювати зміст вивченої ознаки; – виділяти в трикутниках елементи для визначення їх подібності за трьома сторонами; – застосовувати формулювання третьої ознаки подібності трикутників для розв’язування задач. Тип уроку: засвоєння […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Паралельне перенесення та його властивості Геометрія Рух Паралельне перенесення та його властивості Перетворення фігури F, при якому довільна її точка з координатами переходить у точку , де a і b – одні й ті самі для всіх точок, називається Паралельним перенесенням. Теорема. Паралельне перенесення є рухом. При паралельному перенесенні пряма переходить у паралельну пряму (або в себе) (див. рисунок). Існування […]...
- Переміщення та його властивості. Рівні фігури УРОК № 33 Тема. Переміщення та його властивості. Рівні фігури Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13]. Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення […]...
- КООРДИНАТНА ПРЯМА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 22. КООРДИНАТНА ПРЯМА У п’ятому класі додатні числа і число 0 ви позначали на координатному промені (мал. 88). Продовжимо координатний промінь ОХ за його початок вліво. На добудованому промені нанесемо таку саму шкалу, як і на промені ОХ (мал. 89). Дістали координатну пряму. Точка О називається […]...
- ДОДАВАННЯ 0 І ДО 0. ВІДНІМАННЯ 0 І РІВНИХ ЧИСЕЛ. КРУГ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 35. ДОДАВАННЯ 0 І ДО 0. ВІДНІМАННЯ 0 І РІВНИХ ЧИСЕЛ. КРУГ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР Мета: ознайомити учнів із властивостями додавання й віднімання 0, віднімання рівних чисел; розвивати мислення; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ ВИВЧЕНОГО […]...