Показникові рівняння
Математика – Алгебра
Степенева функція
Показникові рівняння
Показниковими рівняннями називають такі рівняння, в яких невідоме входить лише до показників степенів при сталих основах.
Розв’язування показникових рівнянь
1. Розв’язування зведенням до спільної основи
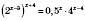 ,
,
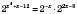 ,
,
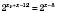 ,
,
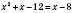 ,
,
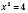 , x = ±2.
, x = ±2.
Відповідь: x1 = 2; x2 = -2.
2. Показникові рівняння, що мають показники з однаковою
Очевидно, що
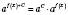 , де C – const,
, де C – const, 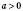 .
.1)
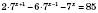 .
.Винесемо за дужки спільний множник лівої частини
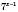 :
: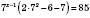 ,
,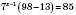 ,
,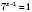 ,
,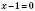 ,
,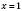 .
.Відповідь: 1.
2)
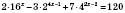 .
.Зведемо всі степені до спільної основи 2.
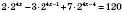 ,
,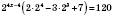 ,
,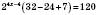 ,
,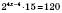 ,
,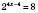
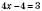 ,
,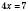 ,
,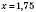 .
.Відповідь: 1,75.
3. Показникові рівняння, що зводяться до квадратних
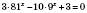 ,
,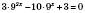 .
.Нехай
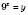 ,
, 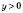 .
.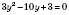 ;
;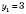 .
. 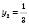 .
.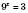 ;
; 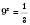 ;
;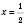 .
. 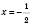 .
.Відповідь:
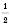 ;
; 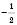 .
.4. Однорідні показникові рівняння
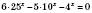 .
.Зверніть увагу, що
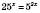 ,
, 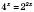 ,
, 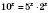 . Отже,
. Отже, 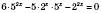 .
.Усі члени лівої частини цього рівняння мають степінь 2х, тобто рівняння однорідне. Поділимо обидві частини його на
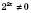 :
: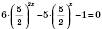 .
.Нехай
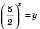 ,
, 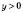 .
.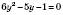 ;
;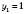 ;
; 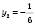 не задовольняє умову
не задовольняє умову 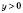 .
.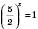 ;
; 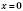 .
.Відповідь: 0.
5. Рівняння, які одночасно містять
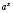 і
і 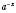 .
.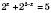 .
.Помножимо обидві частини рівняння на
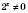 :
: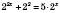 .
.Нехай
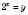 ,
, 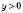 .
.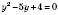 ;
;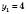 .
. 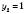 .
.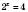 ;
; 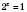 ;
;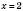 .
. 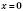 .
.Відповідь: 2; 0.
6. Показникові рівняння, які містять обернені вирази
Зверніть увагу: в рівняннях можна зустріти вирази, добуток яких дорівнює 1, наприклад:
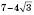 і
і 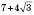 ;
; 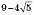 і
і 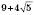 і т. д.
і т. д.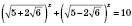 .
.Нехай
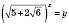 ,
, 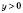 .
.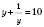 ,
,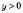 , отже, на y можна помножити обидві частини рівняння.
, отже, на y можна помножити обидві частини рівняння.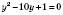 ,
,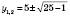 ,
,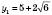 ,
, 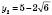 .
.1)
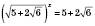 ,
, 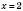 .
.2)
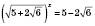 ,
,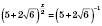 ,
,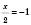 ;
; 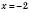 .
.Відповідь: 2; -2.
7. Для розв’язування деяких рівнянь зручно використовувати монотонність показникової функції
1)
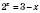 .
.Очевидно, що
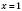 є коренем рівняння. Функція
є коренем рівняння. Функція 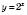 є зростаючою, а функція
є зростаючою, а функція 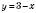 – спадна. Отже, рівняння не може мати більш ніж один корінь.
– спадна. Отже, рівняння не може мати більш ніж один корінь.Відповідь: 1.
2)
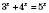 ;
; 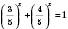 .
.Функція
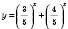 є сумою двох зростаючих функцій, тобто є зростаючою на R. Права частина рівняння 1 – стала величина. Отже, рівняння не може мати більш ніж один корінь.
є сумою двох зростаючих функцій, тобто є зростаючою на R. Права частина рівняння 1 – стала величина. Отже, рівняння не може мати більш ніж один корінь.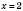 є коренем рівняння.
є коренем рівняння.Відповідь: 2.
Розв’язування показниковостепеневих рівнянь
Показниково-степенева функція має вигляд 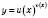 . Її область визначення знаходимо, розглядаючи три випадки:
. Її область визначення знаходимо, розглядаючи три випадки:
1) 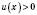 ;
; 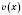 – будь-яке число;
– будь-яке число;
2) 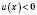 ;
; 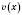 – ціле число;
– ціле число;
3) 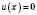 ;
; 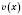 – ціле додатне число.
– ціле додатне число.
Приклад
Розв’язати рівняння:
а) 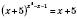 .
.
Розглянемо випадки:
1) 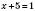 ,
, 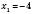 .
.
2) 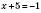 ,
, 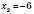 .
.
3) 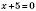 ,
, 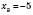 .
.
4) 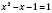 ;
; 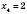 ,
, 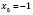 .
.
Перевіркою переконуємося, що всі знайдені корені задовольняють рівняння.
Відповідь: –4; –6; –5; 2; –1.
б) 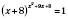 .
.
1) 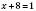 ,
, 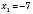 .
.
2) 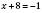 ,
, 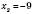 .
.
3) 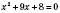 ;
; 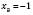 ,
, 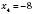 .
.
Перевірка
1) 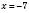 ,
, 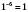 .
.
2) 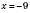 ,
, 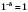 .
.
3) 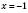 ,
, 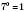 .
.
4) 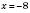 ;
; 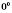 не має змісту.
не має змісту.
Відповідь: –7; –9; –1.
Розв’язування показникових нерівностей
В основі розв’язування показникових нерівностей лежить монотонність показникової функції, яка залежить від значення основи. Способи розв’язування аналогічні способам розв’язування показникових рівнянь, але часто приводять до системи нерівностей, бо треба врахувати умову 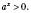
Приклади
1) 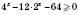 .
.
Нехай 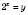 ,
, 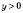 .
.
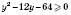 ;
; 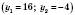 .
.
Дістанемо систему нерівностей:
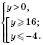

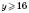 ;
; 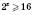 .
.
Показникова функція 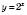 з основою
з основою 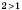 є зростаючою на R.
є зростаючою на R.
Отже, 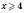 .
.
Відповідь: 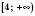 .
.
2) 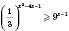 ;
;
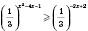 .
.
Показникова функція 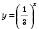 з основою
з основою 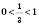 є спадною на R, тому дістанемо:
є спадною на R, тому дістанемо:
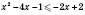 ,
, 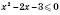 ,
,
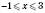 .
.
Відповідь: 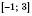 .
.