Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Правильні многокутники

Правильні многокутники

УРОК № 17

Тема. Правильні многокутники

Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач.

Тип уроку: комбінований.

Наочність і обладнання: табл. 4.

Вимоги до рівня підготовки учнів: формують означення правильного многокутника; застосовують вивчені означення до розв’язування задач.

Хід уроку

І. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань

та відповісти на запитання, які виникли в учнів під час виконання домашніх завдань.

ІІ. Аналіз результатів тематичної контрольної роботи № 1

ІІІ. Повторення й узагальнення знань учнів про многокутники

Фронтальна бесіда

1. Сформулюйте означення многокутника; вершин многокутника; сторін многокутника; діагоналей многокутника. 2. Які многокутники вам відомі? 3. Скільки утворюється трикутників, якщо в n-кутнику (n > 3) провести всі його діагоналі з однієї вершини? 4. Що таке кут многокутника? зовнішній кут многокутника? 5. Чому дорівнює сума кутів опуклого n-кутника? 6. Чому дорівнює сума зовнішніх кутів опуклого

многокутника? 7. В опуклого многокутника всі зовнішні кути прямі. Який це многокутник? 8. Чи можна побудувати чотирикутник з двома прямими і двома тупими кутами? 9. Чи може найменший кут чотирикутника становити 91°? 10. Чи можна побудувати опуклий п’ятикутник, усі кути якого прямі? Відповідь поясніть.

IV. Поетапне сприймання й усвідомлення нового матеріалу

Означення правильного многокутника

Серед розмаїття опуклих многокутників виділяють многокутники, у яких усі сторони рівні й усі кути рівні. Такі многокутники називають правильними.

Завдання класу

1) Який трикутник є правильним? 2) Який чотирикутник є правильним? 3) Знайдіть кути правильного шестикутника. 4) Скільки сторін має правильний многокутник, зовнішній кут якого становить 18°? 5) Знайдіть градусну міру кута правильного п-кутника. 6) Знайдіть градусну міру зовнішнього кута правильного п-кутника. 7) Скільки сторін має правильний многокутник, якщо кут при його вершині дорівнює 108°?

Повторення відомостей про вписані й описані трикутники

Фронтальна бесіда

Запитання до класу з використанням табл. 4.

1) Яке коло називається описаним навколо трикутника? Що можна сказати про такий трикутник (по відношенню до кола)? 2) Чи можна описати коло навколо будь-якого трикутника? 3) Де міститься центр кола, описаного навколо трикутника? 4) Яке коло називається вписаним у трикутник? Що можна сказати про такий трикутник (по відношенню до кола)? 5) Чи можна вписати коло в будь-який трикутник? 6) Де міститься центр кола, вписаного в трикутник?

Таблиця 4

Вписані й описані трикутники

Вписані трикутники

Правильні многокутники

Правильні многокутники

Правильні многокутники

Описані трикутники

Правильні многокутники

Правильні многокутники

Правильні многокутники

Означення вписаних і описаних многокутник

Многокутник називається вписаним у коло, якщо всі його вершини лежать на цьому колі.

Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до цього кола.

Запитання до класу

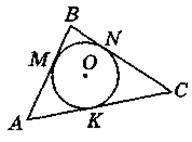
1) Де міститься центр кола, описаного навколо многокутника? Чому? 2) Чи завжди можна описати коло навколо даного многокутника? 3) Побудуйте прямокутник та опишіть коло навколо нього. 4) Де міститься центр кола, вписаного в многокутник? Чому? 5) Чи завжди можна вписати коло в даний многокутник? 6) Побудуйте ромб та впишіть у нього коло. 7) Побудуйте правильний чотирикутник. Впишіть в нього коло й опишіть коло навколо нього.

Вивчення теореми

Теорема. Правильний многокутник є вписаним у коло й описаним навколо кола.

Доведення

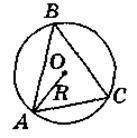
Нехай А і В – дві сусідні вершини правильного многокутника (рис. 72).

Правильні многокутники

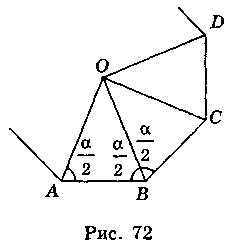
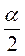Проведемо бісектриси кутів А і В, які перетинаються в точці О. Трикутник АОВ – рівнобедрений (Правильні многокутникиOAB = Правильні многокутникиОВА = Правильні многокутники, де? – кут правильного многокутника). Сполучимо точку О з вершиною С, що є сусідньою з вершиною В. ?АВО = = ?СВО (за першою ознакою рівності трикутників).

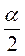Із рівності трикутників випливає, що трикутник ОВС – рівнобедрений з кутом Правильні многокутникиC = Правильні многокутники, тобто CO – бісектриса кута С.

Потім сполучимо точку О із вершиною D, що є сусідньою з вершиною С, і доводимо, що трикутник COD – рівнобедрений і DO – бісектриса кута D і т. д.

Отже, ?ABO = ?BCO = ?CDO = … . Усі ці трикутники мають рівні бічні сторони і рівні висоти, проведені до їхніх основ. Звідси випливає, що всі вершини многокутника лежать на колі з центром О і радіусом, що дорівнює бічним сторонам трикутників, а всі сторони многокутника дотикаються до кола з центром О і радіусом, що дорівнює висотам трикутників, проведеним із вершини О. Теорему доведено.

Можна запропонувати учням самостійно довести цю теорему, а потім провести фронтальну бесіду за рис. 72.

Запитання до класу

1. Чому бісектриси кутів А і В перетинаються? 2. ? – кут многокутника. Чому дорівнюють кути ОАВ і ОВА? 3. Визначте вид трикутника АОВ. Обгрунтуйте відповідь. 4. Чому? АВО = ?ВОС, ?BOC = ?COD? 5. Чому OA = OB = OC = OD? Який висновок можна зробити з цієї рівності? 6. Чому висоти трикутників АОВ, ВОС, COD, проведені з точки О, рівні? 7. Як буде розташовуватися коло з центром у точці О і радіусом, що дорівнює висоті трикутника, по відношенню до многокутника? Чому?

Слід зазначити, що з цієї теореми можна сформулювати такі наслідки.

1) Усі бісектриси кутів правильного многокутника перетинаються в одній точці, яка є центром описаного кола. 2) Усі серединні перпендикуляри, проведені до сторін правильного многокутника, перетинаються в одній точці, яка є центром вписаного кола. 3) Центри вписаного й описаного кіл у правильному многокутнику збігаються. 4) Відрізок, що сполучає центр правильного многокутника з серединою сторони многокутника, є радіусом вписаного кола. Цей відрізок називається апофемою правильного многокутника.

Означення центрального кута правильного многокутника

Кут, під яким видно сторону правильного многокутника з його центра, називається центральним кутом многокутника.

Завдання класу

1) Чому дорівнює центральний кут правильного трикутника? 2) Чому дорівнює центральний кут правильного чотирикутника? 3) Чому дорівнює центральний кут правильного n-кутника? 4) Доведіть, що центральний кут правильного n-кутника дорівнює зовнішньому куту цього многокутника.

V. Закріплення й осмислення нового матеріалу

Виконання вправ

1. Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого дорівнює 135°?

Розв’язання

Оскільки 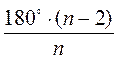Правильні многокутники = 135°, то 180 • (n – 2) = 135n; 180n – 360 = 135n; 180n – 135n = 360; 45n = 360; n = 360 : 45, n = 8.

Відповідь. 8 сторін.

2. Скільки сторін має правильний многокутник, якщо кожний із зовнішніх його кутів дорівнює 36°?

Розв’язання

Оскільки 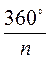Правильні многокутники = 36°, то 360 = 36n; n = 360 : 36, n = 10.

Відповідь. 10 сторін.

3. Доведіть, що взяті через одну вершини правильного 2п-кутника є вершинами правильного п-кутника.

Доведення

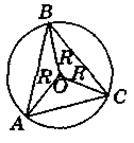
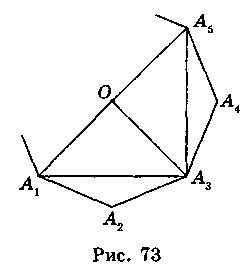
А1А2А3…А2n – даний 2п-кутник, точка О – його центр (рис. 73). Сполучивши вершини А1, A2, A3, …, А2n-1, A1, отримаємо многокутник А1А3А5…А2п-1. Доведемо, що він правильний. ?A1OA3 = ?А3ОА5 = … = ?A2n-1OA1, оскільки А1О = А3О = А5О = … = А2n-1О; Правильні многокутникиA1ОA3 = Правильні многокутникиA3ОA5 =… = Правильні многокутникиA2n-1OA1 = 2Правильні многокутникиA1ОA2. Із рівності цих трикутників маємо: А1А3 = А3А5 = … = А2n-1А1 і Правильні многокутникиA1A3A5 = Правильні многокутникиA3A5A7 = … = Правильні многокутникиA2n-1A1A3 = 2Правильні многокутникиOA1A3. Отже, многокутник A1A3A5…A2n-1 є правильним.

Правильні многокутники

VI. Домашнє завдання

1. Вивчити теоретичний матеріал. 2. Розв’язати задачі. 1) Скільки сторін має правильний многокутник, кожний із внутрішніх кутів якого дорівнює 150°? 2) Скільки сторін має правильний многокутник, якщо кожний із зовнішніх його кутів дорівнює 24°? 3) Доведіть, що середини сторін правильного п-кутника є вершинами іншого правильного п-кутника.

VII. Підбиття підсумків уроку

Запитання до класу

1. Який многокутник називається правильним? 2. Який многокутник називається вписаним у коло? Описаним навколо кола? 3. Чи завжди можна вписати коло в правильний многокутник? описати коло навколо правильного многокутника? 4. Що таке центр правильного многокутника? апофема? 5. Що таке центральний кут правильного многокутника? Чому він дорівнює?


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Правильні многокутники Геометрія Многокутники Правильні многокутники Опуклий многокутник називається Правильним, якщо в нього всі сторони рівні й усі кути рівні. Многокутник називається Вписаним у коло, якщо всі його вершини лежать на деякому колі. Многокутник називається Описаним навколо кола, якщо всі його сторони дотикаються до деякого кола. Теорема 1. Правильний опуклий многокутник є вписаним у коло й описаним […]...

  2. Формули радіусів вписаних і описаних кіл правильних многокутників УРОК № 18 Тема. Формули радіусів вписаних і описаних кіл правильних многокутників Мета уроку: Виведення формул для радіусів вписаних і описаних кіл правильного многокутника. Формування вмінь застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: табл. 5, 6. Вимоги до рівня підготовки учнів: записують і пояснюють формули радіусів вписаного та описаного кіл […]...

  3. Побудова правильних многокутників УРОК № 19 Тема. Побудова правильних многокутників Мета уроку: ознайомлення учнів з правилами побудови правильних многокутників (зокрема трикутників, чотирикутників і шестикутників). Тип уроку: комбінований. Вимоги до рівня підготовки учнів: будують правильний трикутник, чотирикутник і шестикутник. Хід уроку І. Перевірка домашнього завдання Двоє учнів відтворюють за відкидними дошками розв’язування домашніх задач 1 і 2, а в […]...

  4. Многокутники Геометрія Многокутники Ламаною … називається фігура, яка складається з точок , , ,…, і відрізків, що їх послідовно сполучають. Точки , , , …, називаються Вершинами ламаної, а відрізки ; ; …; – Ланками ламаної. Ламана називається Простою, якщо вона не має самоперетинів. Довжиною ламаної називається сума довжин її ланок. На рисунку 1 зображена проста […]...

  5. Многокутники. Розв’язування задач Урок № 49 Тема: Многокутники. Розв’язування задач Мета. Формувати в учнів уміння і навички самостійно застосовувати вивчений матеріал, до розв’язування задач, розвивати навички самостійної пізнавальної роботи, розвивати вміння самостійної роботи, розвивати вміння аналізувати, робити висновки. Форми роботи: математичний диктант, бесіда, розв’язування задач і виконання вправ. Обладнання: лінійка, кольорова крейда, косинець. Тип уроку: урок узагальнення і […]...

  6. Правильні многогранники 862. Якщо у піраміді всі ребра рівні, то з них можна скласти правильний октаедр. АB = а; AM = а; Відповідь: 863. А) так; б) так. 864. А) ні; б) так; в) ні. 865. Якщо з однієї вершини куба провести три діагоналі бічних граней і їх кінці з’єднати відрізками, то утворена піраміда буде тетраедром. 866. […]...

  7. Многокутники. Розв’язування задач і вправ Урок № 47 Тема: Многокутники. Розв’язування задач і вправ Мета. Дати означення ламаної, ввести поняття многокутника, ознайомити з видами многокутників, видами трикутників за сторонами, формувати навички застосовувати вивчений матеріал до розв’язування задач, сприяти формуванню логічного мислення, виховувати вміння самостійно аналізувати і робити висновки. Форми роботи: самостійна робота з підручником, усне опитування “Мозковий штурм”, метод інтерактивної […]...

  8. Властивість точки, рівновіддаленої від сторін многокутника Урок 36 Тема. Властивість точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, вписане в многокутник” Хід уроку 1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку. Нехай ABCD […]...

  9. Сума кутів опуклого многокутника Урок № 43 Тема. Сума кутів опуклого многокутника Мета: закріпити знання змісту понять, вивчених на попередньому уроці. Працювати над засвоєнням учнями змісту та доведення теореми про суму кутів опуклою многокутника. Сформувати вміння: – відтворювати зміст вивченої теореми; – застосовувати теорему під час розв’язування задач на знаходження градусної міри кутів многокутників. Тип уроку: засвоєння нових знань, […]...

  10. Многокутники. Рівні фігури Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 13. Многокутники. Рівні фігури На рисунках 107 і 108 зображено три фігури, кожна з яких обмежена замкненою ламаною, що складається з чотирьох ланок: АВ, ВС, CD і DA. Чим відрізняються межі фігур на рисунку 107 від межі фігури на рисунку […]...

  11. Правильні багатокутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Правильні багатокутники N – число кутів; R1 – радіус описаного кола; R2 – радіус вписаного кола; α – центральний кут; β – внутрішній кут; γ – зовнішній кут; Правильним називається багатокутник, у якому всі сторони і всі внутрішні кути рівні між собою....

  12. Розв’язування задач на застосування властивості точки, рівновіддаленої від сторін многокутника Урок 37 Тема. Розв’язування задач на застосування властивості точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір. Хід уроку 1. Два учні відтворюють розв’язування задач № 46, 47, а в цей час клас пише математичний диктант. 2. Математичний диктант. З центра […]...

  13. Довжина кола і дуги кола УРОК № 20 Тема. Довжина кола і дуги кола Мета уроку: виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Довжина кола і площа круга” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють формули довжини кола і […]...

  14. Властивість точки, рівновіддаленої від вершин многокутнику Урок 32 Тема. Властивість точки, рівновіддаленої від вершин многокутнику Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, описане навколо многокутника”. Хід уроку 1. Перевірити розв’язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку. Розв’язання […]...

  15. Ламана і многокутник Урок № 42 Тема. Ламана і многокутник Мета: сформувати в учнів поняття: – ламана та її елементи; – проста ламана; – многокутник та його елементи; – периметр многокутника; – опуклий многокутник; – внутрішній та зовнішній кути многокутника; – многокутник, вписаний у коло та многокутник, описаний навколо кола. Формувати вміння відтворювати означення вивчених понять; на готовому […]...

  16. Площа ортогональної проекції многокутника Урок 56 Тема. Площа ортогональної проекції многокутника Мета уроку: вивчення теореми про площу ортогональної проекції многокутника, формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 42, 45 на дошці. 2. Фронтальне опитування. 1) Дайте означення кута між двома площинами, які перетинаються. […]...

  17. Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...

  18. Багатокутники. Рівні фігури УРОК 37 Тема. Багатокутники. Рівні фігури Мета: формування поняття многокутника, рівних фігур; навчити розпізнавати многокутники, наводити приклади рівних фігур. Тип уроку: засвоєння нових знань. Обладнання: індивідуальні набори карток для практичної роботи. Хід уроку І. Актуалізація опорних знань Запитання до класу 1. Яка з ліній на рис. 54 є ламаною? замкненою ламаною? Назвіть вершини і ланки […]...

  19. ПОВТОРЕННЯ. ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ Цілі: – навчальна: повторити поняття суми та різниці чисел, закони додавання; відтворити вміння виконувати додавання та віднімання багатоцифрових чисел, розв’язувати задачі, які передбачають додавання та віднімання чисел; повторити означення многокутника та його периметра, класифікацію трикутників; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та […]...

  20. Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...

  21. Багатогранники. Правильні багатогранники 3. Найменша кількість ребер, що сходиться в одній вершині багатогранника – три. 4. В одній вершині багатогранника може сходитися безліч ребер. Розглянемо піраміду з n-кутником в основі. Яким би великим не було число п, Завжди можна побудувати піраміду, основа якої має n + 1 вершин. 5. Розглянемо трикутну піраміду. Кількість її ребер шість. Шість – […]...

  22. Коло, описане навколо трикутника Урок № 49 Тема. Коло, описане навколо трикутника Мета: домогтися засвоєння учнями: – означення кола, описаного навколо трикутника; – властивостей вершин трикутника, вписаного в коло; – змісту теореми про коло, описане навколо трикутника, та схеми її доведення; – наслідку з теореми. Сформувати вміння: – відтворювати формулювання означення та теореми про коло, описане навколо трикутника; – […]...

  23. Коло, вписане в трикутник Урок № 50 Тема. Коло, вписане в трикутник Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї. Сформувати вміння: – відтворювати формулювання означення і теореми про вписане в трикутник коло; – за описом об’єктів розрізняти ті, в яких мова йде про коло, […]...

  24. Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...

  25. Тематичне оцінювання № 4 Урок 43 Тема. Тематичне оцінювання № 4 Мета уроку: перевірка навчальних досягнень учнів з теми “Перпендикулярність прямих і площин у просторі”. Хід уроку Тематичне оцінювання № 4 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 4 Варіант А Варіант 1 1. Побудуйте зображення куба ABCDA1B1C1D1 і запишіть грані куба, які перпендикулярні […]...

  26. Геометричні тіла і многокутники 868. ABCD – тетраедр, 6 ребер, 4 вершини, 4 грані. 869. Многогранник A1A2A3A4A5, 5 граней, 5 вершин, 8 ребер. 870. Многогранник, 5 граней, 6 вершин, 9 ребер. 872. 873. Див. рис. з № 872 S пов. тетр.=36 см2, S грані = 36 : 4 = 9, SABCD = 9 см2, а = ? 874. ABCDA1B1C1D […]...

  27. ПРАВИЛЬНІ І НЕПРАВИЛЬНІ ДРОБИ Цілі: – навчальна: удосконалити вміння розв’язувати задачі, які передбачають використання поняття правильного і неправильного дробу; – розвивальна: формувати вміння аналізувати інформацію, узагальнювати її; – виховна: виховувати свідоме ставлення до навчання; Тип уроку: удосконалення знань і вмінь. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ____________________________________________ ____________________________________________ ____________________________________________ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ 1. Перевірка завдання, заданого […]...

  28. Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Цент­ром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...

  29. Правильні і неправильні дроби. Порівняння дробів Урок № 4 Тема. Правильні і неправильні дроби. Порівняння дробів Мета уроку. Закріпити знання про поняття “правильний дріб”, “неправиль­ний дріб”, правила порівняння дробів з однаковими знаменниками; відпрацювати навички застосування цих знань під час розв’язання задач. Хід уроку І. Перевірка домашнього завдання №№ 985, 989, 993, 1000 можна перевірити під час фронтального опитування. Запитання до класу […]...

  30. Вписаний та описаний чотирикутники – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Вписаний та описаний чотирикутники Якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло: A + C = 180°, B + D = 180°. Якщо суми протилежних сторін чотирикутника рівні, то в нього можна вписати коло: AB + CD = BC + AD...

  31. Многогранні кути 607. Правильний октаедр має 8 граней, кожна з яких – правильний трикутник. Він має 6 чотиригранних кутів. 608. Чотиригранний кут 40°; 70°; 110° і 140° існує неопуклий. 609. Якщо всі плоскі кути чотиригранного кута рівні, то кожний його двогранний кут дорівнює протилежному (октаедр). Площини, які проходять через його протилежні ребра, – перпендикулярні. 611. Якщо у […]...

  32. МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 9. МНОГОКУТНИК ТА ЙОГО ПЕРИМЕТР. РІВНІ ФІГУРИ Подивіться на малюнок 98. Ви бачите, як від точки А послідовно відкладали відрізки АВ, ВС, CD і DE, а точки А і Е сполучили відрізком АЕ. Будь-які два із цих відрізків не перетинаються і не є частинами однієї прямої. […]...

  33. ТРИКУТНИК ТА ЙОГО ВИДИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 10. ТРИКУТНИК ТА ЙОГО ВИДИ Ви знаєте, що трикутник – це окремий вид многокутника. У нього 3 вершини, 3 сторони і 3 кути. Трикутник ABC на малюнку 119 має вершини А, В і С, сторони АВ, ВС i АС, кути ВАС, ABC і АСВ. Серед трикутників […]...

  34. КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...

  35. Заключний урок з теми “Геометричні побудови” Урок № 51 Тема. Заключний урок з теми “Геометричні побудови” Мета: систематизувати та узагальнити знання учнів, набуті в ході вивчення теми “Геометричні побудови”. Систематизувати та узагальнити вміння учнів розв’язувати задачі: – на застосування означення та властивостей кола і його елементів; – на побудову за допомогою циркуля та лінійки; – на метод застосування означення та властивостей […]...

  36. Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...

  37. Поворот УРОК № 36 Тема. Поворот Мета уроку: формування поняття повороту та вивчення властивостей повороту; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують поворот; будує фігури, у які переходять дані фігури при повороті; застосовують вивчені означення і […]...

  38. Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...

  39. Поняття площі многокутника. Площа прямокутника Урок № 44 Тема. Поняття площі многокутника. Площа прямокутника Мета: сформувати в учнів уявлення про площу многокутника, одиницю вимірювання площ, властивості (аксіоми) площ, рівновеликі фігури, рівноскладені многокутники, властивість рівноскладених многокутників та оберненого твердження; працювати над засвоєнням учнями ідеї доведення теореми про площі прямокутника та квадрата. Формувати вміння застосовувати теореми для обчислення площ прямокутника і квадрата. […]...

  40. Розв’язування задач і вправ. Самостійна робота № 6 Урок № 52 Тема. Розв’язування задач і вправ. Самостійна робота № 6 Мета. Формувати в учнів навички і вміння розв’язувати задачі геометричного змісту, удосконалювати вміння працювати в груп, виховувати почуття відповідальності за доручену справу, розвивати логічне мислення, шляхом розв’язування задач. Обладнання: підручник стор 152-153. Тип уроку: урок перевірки знань, навичок і вмінь. Хід уроку I. […]...

Ви зараз читаєте: Правильні многокутники
«
»