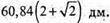Призми
701.
Ні, не існує. 100-кутна призма має 300 ребер, 200 вершин.
703.
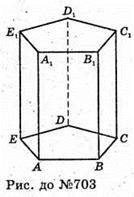
Нехай дано правильну п’ятикутну призму, ∠ABC – двогранний кут при бічному ребрі ВВ1.
∠ABC – лінійний кут двогранного кута при бічному ребрі. ВВ1.
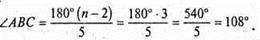
Відповідь: 108
704.
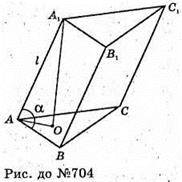
Нехай дано призму, бічне ребро якої АА1 = l, нахилене до площини основи під кутом α. ∠Α1ΑΟ = α. А1O + (ABC).
А1О – висота.
A1Ο = l × sin α.
Відповідь: l sin α.
705.
Діагональні перерізи
Діагональні перерізи правильної п’ятикутної призми не рівні між собою.
706.
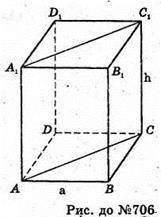
Нехай дано правильну чотирикутну призму, висота якої дорівнює h.
АА1 = h.
AB = ВС = CD = AD = а.
Sбічн. =Pосн × h = 4 × a × h
.
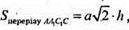де SAA1C1C = AC × C1C,
707.
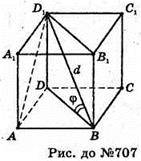
Нехай дано діагональ правильної чотирикутної призми. BD1 = d.
Діагональ ВD1 нахилена до площини основи під кутом ∠D2BD = φ.
BD1 похила, BD – проекція BD1 на площину ABCD.
ΔBDD1 – прямокутний.
DD1 = d × sin φ; BD = d × cos φ.
ABCD – квадрат.
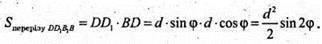
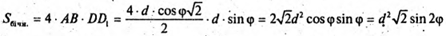
Відповідь: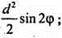 
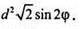
708.
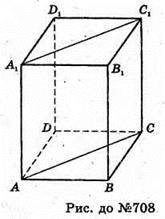
Нехай дано правильну чотирикутну призму, площа основи SABCD = 144 см2; AA1=10 см.
SABCD = a2; a2 =144; а = 12 см.
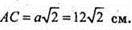
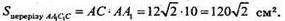
Відповідь: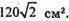 
709.
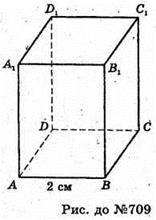
Нехай дано правильну чотирикутну призму.
Sповерхні = 40 см;
Sбічн. = 32 см2;
2Sоснови = Sповерхні – Sбічн. = 40 – 32 = 8 (см 2);
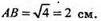
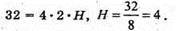
Відповідь: 4 см.
710.
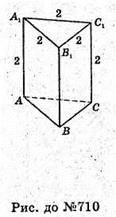
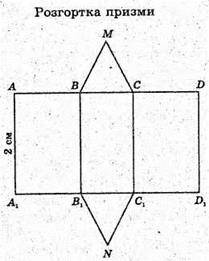
Грані призми AΒA1Β1, ВСС1B1, СDD1С1 – квадрати.
Грані МВС і NB1C1 – рівносторонні трикутники.
АВСА1В1С1 – призма.
Sбічн. = 2 × 3 × 2=12 (см2).
711.
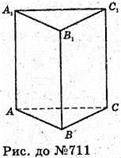
Нехай дано призму АВСА1В1С1 – пряма трикутна призма.
АВ = ВС = АС = А1В1 – A1C1 = АА1 = ВВ1 = СС1 = а
Sбічн. 27 см2.
Sбічн. = Росн. × l, Pосн. – периметр основи, l – бічне ребро.
27 = 3 × а × a, 3а2 =27; а2 =9; а = 3.
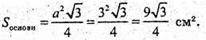
Відповідь: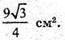 
712.
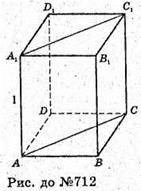
Нехай дано правильну чотирикутну призму, площа діагонального перерізу дорівнює S.
SAA1C1C = S.
Нехай АВ = а; тоді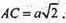 
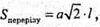
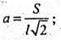
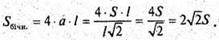
Відповідь: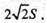 
713.
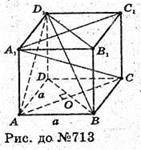
Нехай дано призму, основа якої ромб ABCD, ∠А = 60°,
АВ = ВС = СD = AD = а, бічні грані: ΑΑ1Β1Β; BB1C1C; DD1С1С;
AA1D1D – квадрати.
А1С і D1S – діагоналі призми.
DD1В1В і АА1С1С – діагональні перерізи призми.
ΔАВD – рівносторонній.
BD = AD = АВ = a; ΔАОВ – прямокутний; AO + ОВ.
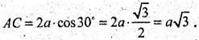
ΑΑ1Β1Β – квадрат. А1А = АВ = а.
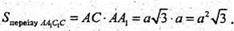
Sперерізу DD1B1B = BD × АА1 = a × а = a 2.
ΔАА1С – прямокутний.
А1С2 = АА12 + АС2 = а2 + 3а2 = 4а2.
А1С = 2а;
ΔDD1B – прямокутний.
D1B2 = DD12 + BD2= a2 + a2 = 2а2;
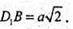
Відповідь: 2а;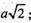 
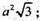а2.
714.
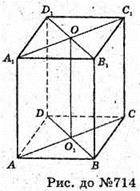
Нехай дано призму, у якої діагональні перерізи А1С1СА і DD1Β1Β перетинаються і мають спільний відрізок ОО1. АА1С1С-паралелограм,
DD1B1B – паралелограм.
АА1 ? С1С; DD1 ? В1В. ОО1 – спільний відрізок. ОО1 ? АА1; ОО1 ? DD1.
ОО1 = АА1 = С1С = D1D = В1В, що й треба довести.
715.
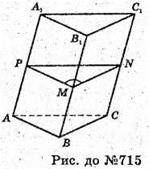
Нехай АВСА1В1С1 – призма. ΔMNP – перпендикулярний переріз призми.
PN = 13 см; PM = 7 см; MN = 8 см.
ΔΡΜΝ – найбільший кут при ребрі призми.
PN2= РМ + MN2- 2РМ × NM cos ∠Μ за теоремою косинусів.
169 = 49 + 64 – 2 × 7 × 8 × cos ∠M;
169 = 113 – 112 cos ∠Μ ;
112cos ∠M = -56;
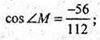
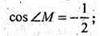
∠Μ = 120°.
Відповідь: ∠Μ = 120°.
716.
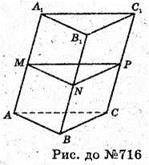
Нехай дано призму АВСА1В1С1, відстань між бічними ребрами MN = 18 см;
МР = 20 см; NP = 22 см; Sбічн. призми = SΔMNP
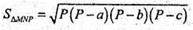
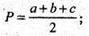
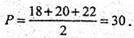
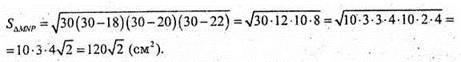
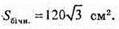
Sбічн = PΔMNP × C1C
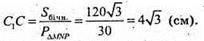
Відповідь: 
717.
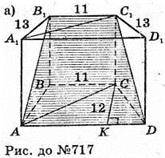
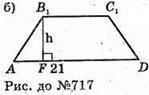
Нехай основою призми є трапеція ABCD, у якої AD = 21 см; ВС = 11 см;
АB = CD = 13 см. Через ребра AD і B1С1 проходить переріз АB1С1D.
PперерізуАА1С1С = 58 см.
AA1
СА + AD. СК – висота трапеції АВСD.
KD = (AD – ВС) : 2 = (21 – 11) : 2 – 5 (см).
ΔАСА -· прямокутний.
ΔС2 = АK2 + СK2. АK = 21 – 5 = 16 (см).
ΔCKD – прямокутний.
СK2 = СD2 – KD2 = 169 – 25 = 144. СK = 12 см.
ΔАСK: АС2 = 162 +122 = 256 + 144 = 400 (см2).
АС = 20 см.
PперерізуАА1С1С = 2AA1 + 2A1C1;
58 = 2 × AA1 + 2 × 20;
58 = 2 × ΑΑ 1 + 40; 2AA1 = 18; AA1 = 9 см.
Sповерхні = Sбічне + Sоснови.
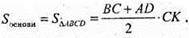
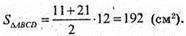
Sбічне = PABCD × AA1 = (13 + 11 + 13 + 21) – 9 = 522 (см2).
Sповн. = 2 × 96 + 522 = 714 (см2).
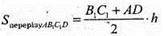
ΔAA1B1 – прямокутний.
AВ12 = AА12 + А1В12; = 169 + 81 = 250.
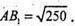
ΔAB1F – прямокутний.
B1,F2 = h2 = AB2 – AF2 = 250 – 25 = 225.
H = B1F = 15.’
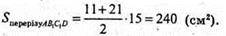
Відповідь: 714 см2; 240 см2.
718.
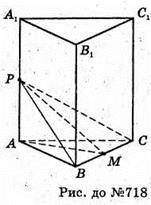
Нехай дано правильну трикутну призму, всі бічні грані якої квадрати, площа бічної поверхні 12 см2; площа однієї грані 12 : 3 = 4 (см2), сторона квадрата 2см.
АВ = АС = ВС = 2 см.
ВВ1 = АА1 = СС1 = 2 см.
∠BMP – кут між площиною основи і площиною, проведеною через ребро основи і середину протилежного ребра.
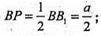
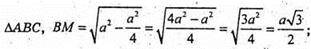
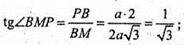
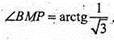
Відповідь: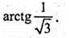 
719.
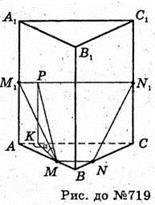
Нехай через середини двох сторін основи правильної трикутної призми під кутом α до основи проведено площину, яка перетинає два бічних ребра в точках M1і N1.
МР + М1N1, KР + АС; МK + АС.
∠BMP = а – кут нахилу площини MM1N1N до площини основи ABC.
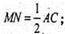
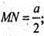MN – середня лінія ΔАВС. M1N1 ? MN ;
M1N1 ? АС. M1N 1 = AC=a.
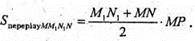
ΔМРK – прямокутний.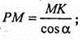 
ΔАМK – прямокутний.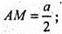 
∠KAM = 60°;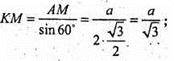 
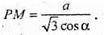
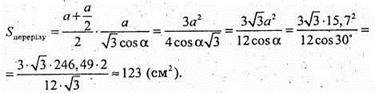
720.
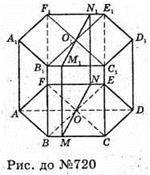
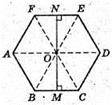
Нехай дано правильну шестикутну призму, площа бічної грані якої дорівнює S. SAA1B1B = S – площа бічної грані правильної шестикутної призми. Переріз MM1N1N перпендикулярний до більшої діагоналі АD і ділить цю діагональ навпіл.
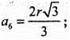R = ОВ = ОС; r = ОМ.
Sбічної грані = a × l, де l = B1B.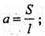 
ΜΜ 1 = l.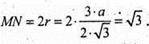 
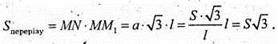
Відповідь: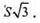 
721.
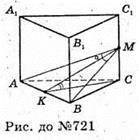
Нехай дано – правильну трикутну призму AВСA1В1С1. Через сторону основи АВ проведено площину АМВ, яка перетинає грань B1BСС1 по прямій ВМ, а грань AA1С1С по прямій AM, ∠AMB = α.
МС + ABC; СK + АВ; АK = KВ, тоді за теоремою про три перпендикуляри
МK + AB.
∠МКС – кут між площиною ΔАМВ і площиною ΔАВС.
Нехай АВ = ВС = АС = а, тоді
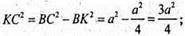
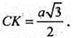
ΔМВK: МK + ВK;
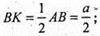
ВМ = AM із рівності прямокутних трикутників. ΔBMC = ΔАМС.
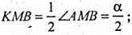
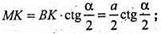
ΔМKС – прямокутний.
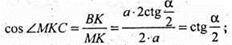
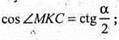
Відповідь: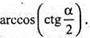 
722.
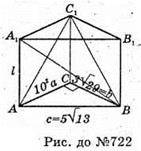
Нехай дано пряму трикутну призму, в· основі якої лежить прямокутний трикутник ΔABC.
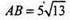– гіпотенуза.
Діагональ грані AA1С1С дорівнює 10 см.
Діагональ грані CC1B1B дорівнює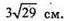 
Діагональ грані ΑΑ1Β1Β дорівнює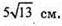 
Нехай сторони основи АВ = с; АС = а; ВС = b; ВВ1 = AA1 = СС1 = l.
ΔАСС1 – прямокутний.
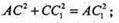
А2 + l2 = 100;
ΔВСС 1 – прямокутний.
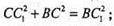
B2 +12 = 261;
ΔАВВ1 – прямокутний.
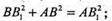
С2 + l2 = 325 ;
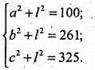
С2 – b2 = 325 – 261; с2 – b2 = а2; а2 = 64; а = 8 см.
64 + l2 =100; l2 = 100 – 64 = 36; l = 6 см.
B2 =261 – 36 = 225; b = 15 см.
С2 = а2 + b2 = 64 + 225 = 289; с = 17 см.
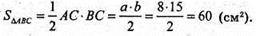
S бічн. = Росн. × l = (АС + ВС + АВ) × АА 1 = (8 +15 +17) × 6 = 240 (см2).
S повн. = Sбічн. + 2Sосновн = 240 +120 = 360 (см2).
Відповідь: 360 см2.
723.
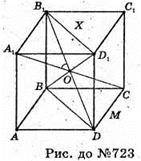
Нехай дано правильну чотирикутну призму ABCDA1B1C1D1i, у якої діагоналі А1С і B1D, B1D + BD1, кут між діагоналями А1С і B1D дорівнює 60°.
∠A1ΟΒ1 – кут між діагоналями B1D і А1С. За умовою B1D + BD1
Отже BB1D1D – квадрат. Тому BD = DD1. Нехай BD = DD1 = а,
Тоді ΔABD – прямокутний. AB2 + AD2=a2; 2АВ2 = а2;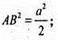 
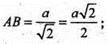
ΔBB1D – прямокутний. Β1D2 = ВВ12 + BD2; Β1D2 = а2 + а2 = 2а ;
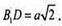
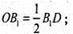
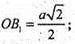
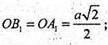
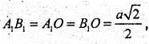
Отже АА1ОВ1 – рівносторонній.
∠A1OB1 – 60°, що й треба було довести.
724.
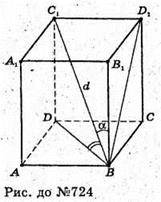
Нехай дано правильну чотирикутну призму, діагональ BD1 = d, діагональ призми утворює з бічною гранню кут α. ∠D1ВС1 = α (кут між прямою BD1 і її проекцією BC1 на площину).
A) ∠D1BD – кут між діагоналлю призми і площиною основи.
ΔВD1С1 – прямокутний. D1С1 = d × sin α; BC1 = d × cos α ;
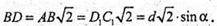
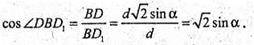
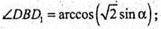
Б) ΔDD1В: DD1 = BD1 × sin ∠DBD1; або
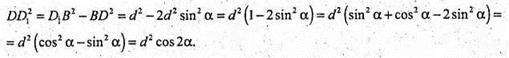
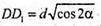
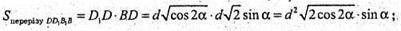
В) площа бічної поверхні:
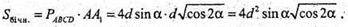
725.
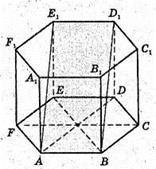
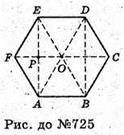
Нехай дано правильну шестикутну призму, кожне ребро якої дорівнює а.
АВ = ВС = DC = ED = EE = a. AΑ1 = BB1 = СС1 = DD1 = EE1 = FF1 = a.
Через сторону нижньої основи і протилежну їй сторону верхньої основи проведено переріз ABD1E1.
Sперерізу = АВ × АЕ1. ABD1E1 – прямокутник. E1F + площині основи. ЕА + АВ.
Е1А + АВ за теоремою про три перпендикуляри.
ΔЕОА – рівнобедрений трикутник. ОЕ = ОА = R = а.
ΔЕОР – прямокутний. ∠ΕΟΡ = 60°;
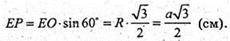
ΔЕ1ЕА – прямокутний, Е1Е + АЕ.
Ε1A2 = Ε1Ε2 + АЕ2 = а2 + 3а2 =4а2; Е1А = 2а.
SперерізуABD1E1 = a × 2а = 2а 2.
Відповідь: 2а2.
726.
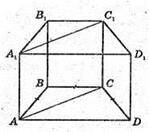
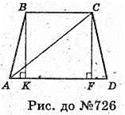
Нехай дано пряму призму, в основі якої лежить трапеція ABCD.
АВ = ВС = СD= 0,5AD.
A1С 1СА – діагональний переріз призми.
Sперерізу = АА1 × АС
Нехай АВ = ВС = CD = а, тоді AD = 2а;
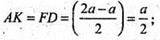
ΔАВK – прямокутний,
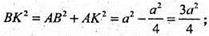
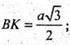
ΔACF – прямокутний,
АС2 = CF2 + AF2;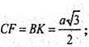 
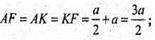
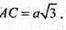
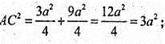
Sбічн. = РAВСD × АА 1; S = (а + а + а + 2а) × l; S = 5al;
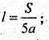
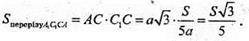
Відповідь: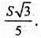 
727.
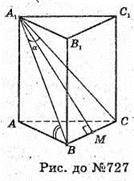
Нехай дано АВСА1В1С1 – правильну трикутну призму.
∠BA1C = α.
ΔΒA1С – рівнобедрений,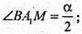 
А1М + ВС. Нехай ВС = а.
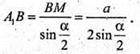
ΔΑ1ΑΒ – прямокутний,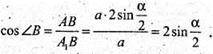 
Відповідь: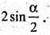 
728.
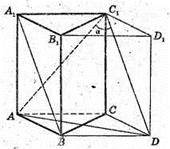
Нехай дано правильну трикутну призму AВСА1В1С1, у якої кут між прямими Α1B і АС, дорівнює α. Бічне ребро АА1 = ВВ1 = СС1 = b. А1В і АС1 – мимобіжні прямі. Проведемо CD? АВ, BD? АС, ABCD – і ромб. Через D проведемо DD1 ? ВВ1.
B1D1 ? BD; C1D1 ? CD. ABDCA1B1D1C1 – чотирикутна призма, в основі якої ромб ABCD. У грані CC1D1D проведемо C1D? A 1B, ∠AC 1D = α.
Нехай АВ = BD = a; ΔOBD – прямокутний.
∠B = 120°,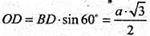 
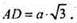ΔAC1D – рівнобедрений, АС1 = DC1 = х.
За теоремою косинусів маємо: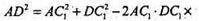 
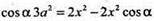
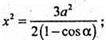
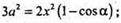
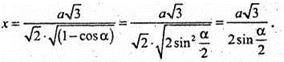
ΔАА1С1 – прямокутний,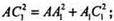 
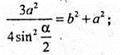
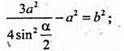
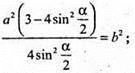
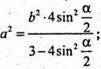
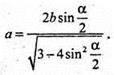
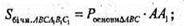
Sбічн. = 3а × b;
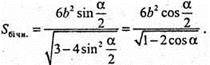
729.
A)
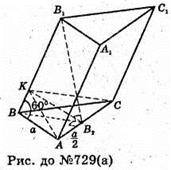
Нехай дано похилу призму АВСА1В, С1, основою якої є правильний трикутник ΔABC, AB = АС = ВС = а. Вершина B1 проектується на середину сторони АС. Бічні ребра утворюють із площиною основи кут 60°.
В1В2 + АС;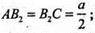 
∠B1ΒB2 = 60°.
ΔАВВ2 – прямокутний, В1В2 + ВВ2.
ΔВВ1В2 – прямокутний.
Із ΔАВВ2 за теоремою Піфагора:
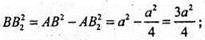
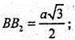
ΔВ1ВВ2 – прямокутний: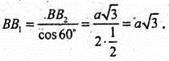 
У площині (В1ВВ2) проведемо В2K + ВВ1. АK + ВВ1; KС + ВВ1.
ΔАKС – перпендикулярний переріз призми АВСА1В1С1.
Із ΔВKВ2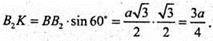 
Із ΔАKВ2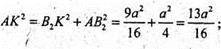 
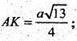
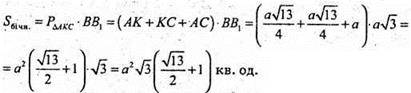
Б)
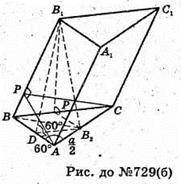
Нехай дано похилу призму, основою якої є правильний ААВС зі стороною a.
В 1 проектується на середину сторони АС, точку В2. Двогранні кути при ребрах AB і ВС дорівнюють 60°.
В1В2 + АС, отже, В1В2 + площині ААВС.
Проведемо В2D + АВ, тоді за теоремою про три перпендикуляри B1D + АВ, отже, ∠B1DB2 = 60° – лінійний кут двогранного кута при ребрі АВ.
Аналогічно В2Р + ВС, В1Р + ВС, ∠В1РВ2 – лінійний кут двогранного кута при ребрі ВС.
∠В1РВ2 = ∠Β1DΒ2 = 60°.
Δ AB2D – прямокутний, ∠A = 60°;
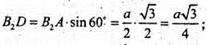
Δ B2DB2- прямокутний.
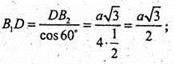
SABB1A1 = B1D × АВ = АР × ВВ1, де АР + ВВ1.
АР і B1D – висоти бічної грані – паралелограма ABB1A1.
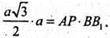
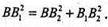
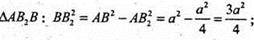
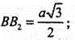
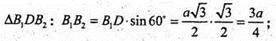
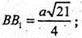
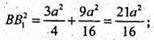
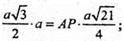
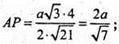АР = PC.
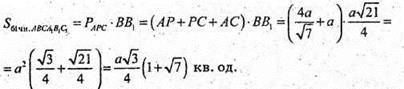
730.
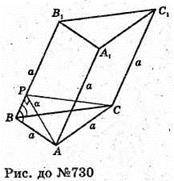
Нехай дано похилу призму АВСА1В1С1, усі ребра якої дорівнюють а.
АВ = АС = ВС = А1В1 = А1С1 = В1С1 = а. ВВ1 = АА1 = СС1 = a.
∠ Β1ΒΑ = ∠ B1BC = α.
Sповерхні = 2Sоснови + Sбічн.
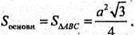
ΔАВС – рівносторонній.
Проведемо АР + ВВ1; CP + BВ1,
ΔАРС – перпендикулярний переріз призми AВСA1В1С1.
ΔАВР: AP = AB × sin α = a × sin α.
РΔАВС = АР + РС + АС.
РΔАВС = a × sin α + a × sin α + a = 2asin α + a = a(2sin α + 1)
Sбічн.= BB1 × P ΔАPС = a2(2sin α +1).
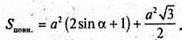
Відповідь: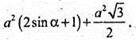 
731.
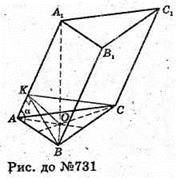
Нехай дано трикутну призму АВСА1В1С1, у якої кожна сторона основи дорівнює а. АВ = ВС = АС = а; А1В1 = В1С1 – А1С, = а. Проекцією вершини А1 основи
А1В1С1 є точка О – центр основи ΔАВС.
ΔАВС – рівносторонній. АВ = ВС = АС = а;
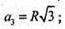
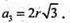
ОB – радіус описаного кола.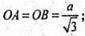 
∠А1АО = а. ΔAΑ1Ο – прямокутний.
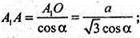
АА1 – ребро призми.
ОК + АА1. ΔАKО – прямокутний.
OK = АО sina;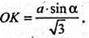 
ВK + АА,
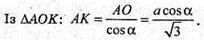
Проведемо ВK + AΑ1, ВK2 = АВ2 – АK2.
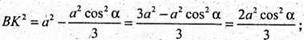
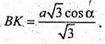
Sбічн. ABCA1B1C1 = PΔBKC =(ВK + KС + ВС) × АА1.
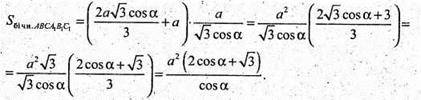
732.
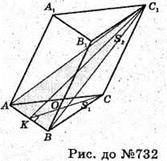
Нехай дано правильну трикутну призму АВСА1В1С1. Площа основи SΔABC = S1.
Переріз проходить через ребро нижньої основи АВ і протилежну вершину С1 верхньої основи ΔА1В1С1. SΔBC1 = S2.
SΔАВС = S1. Нехай АВ = ВС = АС = а,
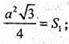
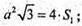
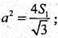
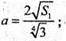
А – ребро основи.
ΔВСK – прямокутний. СК + ВС.
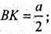ВС = а;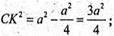 
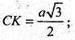
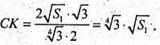
SΔABC1 = S2;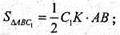 
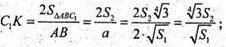
ΔС1СK – прямокутний; С1С + (ABC), С1С + KС.
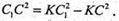
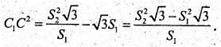
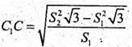
Sбічн. АВСА1В1С1 = Pоснови × CC1.
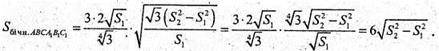
Відповідь: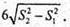 
733.
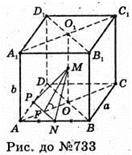
Нехай дано правильну чотирикутну призму ABCDA1B1C1D1, у якої сторона основи АВ = ВС = DC = AD = а; бічне ребро АА1 = ВВ1 = СС1 = DD1 = b. Через середину відрізка O1O, який з’єднує центри О2 і О основ і середини двох суміжних сторін, основи AD і АВ, проведено площину PMN. AN = BN; АР = PD; O1М = ОМ.
MO + ABCD; AO + BD; PN – середня лінія ΔABD.
PN? BD,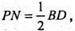 
PN + АО; за теоремою про три перпендикулярі MF + АО,
Отже, ∠MFO – кут між площиною перерізу APMN і площиною основи.
ОО1 = СС1 = b.
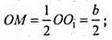
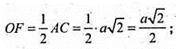
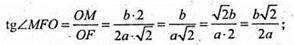
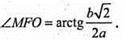
Відповідь: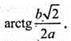 
734.
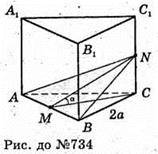
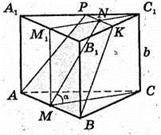
Нехай дано правильну трикутну призму ABCA1B1C1, у якої сторона основи
АВ = ВС = АС = 2а; бічні ребра АА1 = ВВ1 = СС1, = b. Через сторону АВ нижньої основи під кутом α до неї проведено площину ABN.
NC + ABC; CM + АВ; NM + АВ. ∠NMC = α – кут між площинами ABC і ABN.
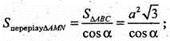
АРKВ – переріз.
АРKВ – трапеція.
РK? A1В1; АВ + A1В1, отже, РK? АВ1. СМ + AB; NM + AB; ∠NMB = α, кут між площиною ААВС і площиною трапеції ΔВРК. ΜΝ – висота трапеції.
735.
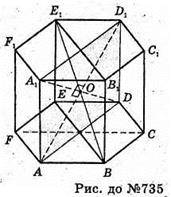
Нехай дано правильну чотирикутну призму. Через середину більшої діагоналі перпендикулярно до неї проведено переріз. Висота призми в 2 рази більша за сторону основи, площа бічної поверхні 48 см2. Висота призми АА1 = 2АВ. Нехай АВ = а, тоді АА1 =2а.
AA1D1D – діагональний переріз призми, в якому AD = 2а, АА1 = AD, отже,
ΑΑ1D1D – квадрат, AD1 – діагональ призми.
Через середину діагоналі АD1 точку О проведено перпендикулярний переріз.
Sбічної поверхні = Pоснови × h = PАBCDEF × АА1 = 6a × 2a = 12a2;
12a2 = 48; а2 = 4; а = 2, отже, АВ = 2 см; АA 1 = 4 см.
Sперерізу = 2а × а = 2a2 = 2 × 22 = 8 (см2).
736.
Місце центроїда всіх вершин правильної призми – точка перетину діагоналей цієї призми.
737.
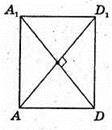
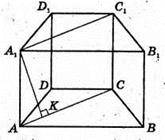
Нехай дано призму, в основі якої трапеція ABCD. Основи призми ABDCA1B1D1C1 – рівні трапеції ABCD і A1B1C1D1, паралельні сторони AB і CD, непаралельні – AD і ВС.
ΑΒ = Α1Β1= 8,8 дм:
DC = D1C1 = 5,6 дм:
AD = ВС = 3,4 дм.
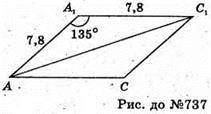
АА1С1С – діагональний переріз, перпендикулярний до основи, і є ромбом.
AA1C1C – ромб.
АА1 = АС = СС1 = А1С1; ∠A1AC = 45°.
Розглянемо трапецію ABCD.
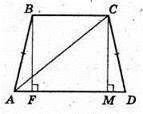
Проведемо BF + AD; CM + AD.
ΔABF = ΔDCM (АВ = CD; BF = CM).
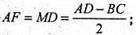
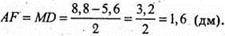
ΔABF – прямокутний.
BF2 = АВ2 – AF2 = 3,42-1,62 = 9;
BF2 = 9 (дм2). BF = 3 дм.
ΔACM – прямокутний.
АС2 = АМ2 + МС2; АМ = AF + FM = 1,6 + 5,6 = 7,2.
АС2 = 7,22 + 9 = 60,84.
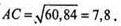
AA1C1C – ромб.
A1K + AС; А1K – висота ромба, А1K – висота похилої призми ABDCA1B1D1C1.
ΔΑΑ1K – прямокутний.
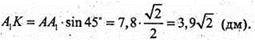
Отже, висота призми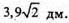 
Діаметр призми АС1 – діагональ призми. Розглянемо ромб АА1С1С.
∠A = 45°; ∠A1 =135°.
Із ΔAА1С1 за теоремою косинусів маємо:
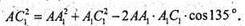
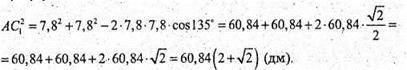
Відповідь: 
(1 votes, average: 5.00 out of 5)
Loading...