Промінь. Кут. Вимірювання кутів
§ 1. Найпростіші геометричні фігури та їхні властивості
3. Промінь. Кут. Вимірювання кутів
Практичні завдання
49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM.
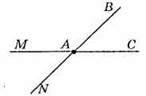
50. Промені AB і ВА не е доповняльними, оскільки вони не мають спільного початку.

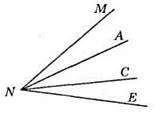
51. На рисунку зображено кути: MNA, MNC, MNE, ANC, ANE, CNE.
52.
53. 1) AB
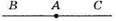
2) AB i BA.

3) АВ i ВС.
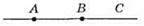
Вправи
54. 1) Промені з початком у точці М: MC, MF, MD, ME.
2) Пари доповняльних променів з початком у точці К: КА і КВ; КЕ і КМ.
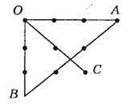
55. Промені, зображені на рисунку: ОА, OB, ОС, OD, МА, MB.
Доповняльні промені з початком у точці О: О А і OB; OC i OD.
56. 1) Ні; 2) так; 3) ні; 4) так; 5) так; 6) так; 7) ні; 8) ні.
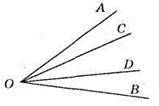
57. ∠ВАС, ∠BAD, ∠BAE, ∠CAD, ∠CAE, ∠DAE.
58. 1) Бісектрисою кута АОС є промінь OB. Бісектрисою кута DOF є промінь ОЕ. Бісектрисою кута BOF є промінь OD.
2) Промінь ОС є бісектрисою кутів BOD і АОЕ.
59. 1) Кути АОС і ВОС можна сумістити
2) Кути АОС і АОВ не можна сумістити накладанням, бо вони не рівні.
60. 1) ∠ABC = ∠ABD + ∠CBD = 54° + 72° = 126°.
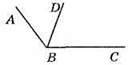
Відповідь: 126°.
2) ∠CBD = ∠ABC – ∠ABD = 158° – 93°= 65°.
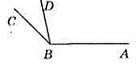
Відповідь: 65°.
61. ∠MOP = ∠MOK – ∠POK= 172° – 85° = 87°.
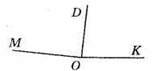
Відповідь: 87°.
62. 1) Ні, кут може бути прямим; 2) ні, кут може бути прямим або гострим; 3) так; 4) ні, може бути гострим (15° + 10° = 25°); 5) так; 6) ні, може бути розгорнутим.
63. ∠COM = ∠BOM – ∠BOC = 90° – 74° = 16°;
∠AOC = ∠AOM – ∠COM = 62° – 16° = 46°.
Відповідь: 46°.
64. ∠FCP = ∠ACP – ∠ACF = 180° – 158° = 22°;
∠TCF = ∠TCP – ∠FCP = 134° – 22° = 112°.
Відповідь: 112°.
65. Нехай ∠FEM = х°, тоді ∠MEC = х° + 18°, тоді маємо рівняння:
Х + х + 18 = 152 (бо ∠FEM + ∠MEC = ∠CEF), звідси 2х + 18 = 152; 2х = 152 – 18; 2х = 134; х = 134 : 2; х = 67, тоді х + 18 = 67 + 18 = 85. Отже, ∠FEM = 67°, ∠MEC = 85°.
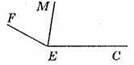
Відповідь: 85° і 67°.
66. Нехай ∠BAK = х°, Toдi ∠DAK = 7х°. За умовою ∠DAK + ∠BAK = ∠BAD, тоді маємо рівняння х + 7х = 72, звідси 8х = 72; х = 72 : 8; х = 9, тоді 7х = 7 х 9 = 63. Отже, ∠BAK = 9°, ∠DAK = 63°.
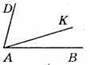
Відповідь: 9° і 63°.
67. 1) Якщо ∠ABC = 1, то ∠MKE = 2, ∠STK = 5.
2) Якщо ∠MKE = 1, то ∠ABC = 1/2; ∠STK = 2•1/2.
68. Оскільки ВС = AB + АС (8 см = 3,2 см + 4,8 см), то точки А, В, С лежать на одній прямій, причому точка А лежить між точками В і С. Отже, промені AB i АС є доповняльними.

69. ∠ABE = ∠EBF = ∠FBC = 90°: 3 = 30°.
∠ABD = 1/2∠ZABE = 1/2 • 30° = 15° (бо BD – бісектриса кута ABE).
∠CBK = 1/2∠CBF = 1/2 • 300 = 15° (бо BK – бісектриса кута CBF).
∠DBK = ∠ABC – ∠ABD – ∠CBK = 90° – 15° -15° = 60°.
Відповідь: 60°.
70. Нехай ∠AOC = ∠COD = ∠DOF = 2х°, тоді ∠AOB = х°, ∠FOE = х°. За умовою задачі ∠BOE = ∠AOF – ∠AOB – ∠FOE, тоді маємо рівняння 72 = 6х – х – х, звідси 4x = 72; x = 72 : 4; x = 18, тоді 6х = 6 х 18 = 108. Отже, ∠AOF = 108°.
Відповідь: 108°.
71. Нехай ∠AOB = ∠DOC = x°, тоді ∠AOC = ∠AOD – ∠DOC = 180° – x°, ∠DOB = ∠AOD – ∠AOB = 180° – x°. Отже, ∠AOC = ∠DBO.
Відповідь: так, ∠AOC = ∠DOB.
72. Нехай ∠FOK = ∠MOE – x°, тоді ∠FOM = ∠FOE – ∠MOE = ∠FOE – x°, ∠KOE = ∠FOE – ∠FOK = ∠FOE – x°. Отже, ∠FOM = ∠KOE.
Відповідь: так, ∠FOM = ∠KOE.
73. ∠CBK = ∠ABC – ∠ABK = 180° – 146° = 34°. ∠CBD = 2∠CBK = 2 x 34° = 68°.
Відповідь: 68°.
74. ∠CBK = 1/2∠CBD = 1/2 • 56° = 28°.
∠ABK = ∠ABC – ∠CBK=180° – 28°=152°.
Відповідь: 152°.
75. 1) За 1 годину хвилинна стрілка повертається на 360°, тоді за 1 хвилину хвилинна стрілка повертається на 360° : 6 = 6°.
Відповідь: 6°.
2) За 12 годин годинна стрілка повертається на 360°, тоді за 1 годину вона повертається на 360° : 12 = 30°, а за 1 хвилину вона повертається іта 30° : 60 = 0,5°.
Відповідь: 0,5°.
76. 1) Якщо стрілки годинника показують 3 год, то вони утворюють прямий кут (90°).
2) Якщо стрілки годинника показують 6 год, то вони утворюють розгорнутий кут (180°).
3) Якщо стрілки годинника показують 4 год, то вони утворюють кут 120°.
4) Якщо стрілки годинника показують 11 год, то вони утворюють кут 30°.
5) Якщо стрілки годинника показують 7 год, то вони утворюють кут 150°.
77. 1-й випадок – промінь ВС лежить між сторонами кута ABD.
∠ABD = ∠ABC + ∠CBD = 30о + 80° = 110°.
2-й випадок – промінь ВА лежить між сторонами кута CBD.
∠ABD = ∠CBD – ∠ABC = 80° – 30° = 50°.
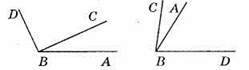
Відповідь: 110° або 50°.
78. 1-й випадок – промінь ON лежить між сторонами кута МОК.
∠MOK = ∠MON + ∠NOK = 120° + 43° = 163°.
2-й випадок – промінь ОК лежить між, сторонами кута MON.
∠MOK = ∠MON – ∠KON = 120° – 43° = 77°.
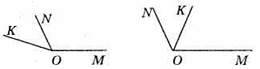
Відповідь: 163° або 77°.
79. Нехай ∠ABC = 90°, ВМ і BN – бісектриси кутів ABD і CBD, тоді ∠MBD = 1/2∠ABD, ∠DBN = 1/2∠DBC.
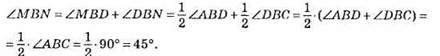
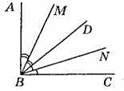
80. Побудувавши розгорнутий кут ABC та відклавши шаблоном два кути по 70°, отримаємо ∠ABN = 40°.
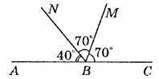
81. 1) Відклавши шаблоном два кути по 40°, отримаємо кут ABD, причому ∠ABD = 80°.
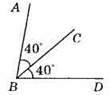
2) Відклавши шаблоном чотири кути по 40°, отримаємо кут ABF, причому ∠ABF = 160°.
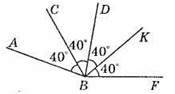
3) Побудувавши розгорнутий кут ABC та відклавши шаблоном чотири кути по 40°, отримаємо кут АВР, причому ∠ABP = 20°.
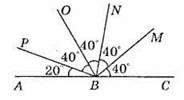
82. Відклавши від довільного променя ОА 14 разів кут в 13°, отримаємо кут AОВ, причому ∠BOC = 2°, де ОС – промінь доповняльний до променя ОА.
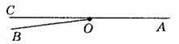
83. 1) Відклавши від довільного променя ОА 19 разів кут в 19°, отримаємо: 19° х 19 = 361°, тоді ∠AOC = 1°.

2) Відклавши від довільного променя ОА 103 рази кут в 7°, отримаємо 7° х 103 = 721°, тоді ∠AOC = 1°.

84. Припустимо, що не існує кута, який менший від 31°, тоді сума всіх кутів, утворених шістьма прямими, буде не менша ніж 31° х 12 = 372°, проте сума всіх кутів дорівнює 2 х ∠AOB = 2 х 180°= 360°. Отже, припущення неправильне. Таким чином, існує кут, менший, ніж 31°.
Спостерігайте, рисуйте, конструюйте, фантазуйте
85. Слід побудувати послідовно відрізки ОА, AB, ВО, ОС.