Головна ⇒ 📌Довідник з математики ⇒ Прямокутний паралелепіпед – Геометричні фігури й величини
Прямокутний паралелепіпед – Геометричні фігури й величини
Математика – Алгебра
Геометричні фігури й величини
Прямокутний паралелепіпед
Прямокутний паралелепіпед (див. рисунок) має 8 вершин, 12 ребер, котрі можна розбити на 3 групи по 4 рівних, а також 6 граней (3 пари рівних між собою прямокутників).
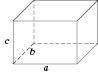
Площа поверхні прямокутного паралелепіпеда дорівнює сумі площ його граней:
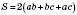 .
.
Об’єм прямокутного паралелепіпеда 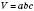 .
.
Коли 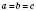 , дістанемо Куб (див. рисунок). Усі ребра куба рівні, усі грані – рівні квадрати.
, дістанемо Куб (див. рисунок). Усі ребра куба рівні, усі грані – рівні квадрати.
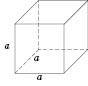
Площа поверхні куба 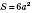 .
.
Об’єм куба 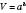 .
.
Related posts:
- Прямокутний паралелепіпед. Куб. Піраміда Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 25. Прямокутний паралелепіпед. Куб. Піраміда Сірникова коробочка, цеглина, дерев’яний брусок, ящик, пенал дають уявлення про геометричну фігуру, яка називається прямокутним паралелепіпедом (рис. 188). Рис. 188 Поверхня прямокутного паралелепіпеда складається із шести прямокутників, які називаються його гранями. Протилежні грані прямокутного паралелепіпеда попарно рівні. […]...
- Прямокутний паралелепіпед та його об’єм Урок № 56 Тема. Прямокутний паралелепіпед та його об’єм Мета. Поглибити знання учнів про прямокутний паралелепіпед та його виміри, закріпити поняття об’єму та його формули, вчити розв’язувати задачі на обчислення площі поверхні та об’єму прямокутного паралелепіпеда. Сприяти виробленню навичок до самостійної навчальної діяльності, виховувати позитивну мотивацію до навчання. Розвивати здібності учнів, усну і письмову культуру […]...
- Прямокутний паралелепіпед і його об’єм Урок 62 Тема. Прямокутний паралелепіпед і його об’єм Мета: навчити розв’язувати задачі практичного і фізичного змісту на обчислення об’ємів прямокутного паралелепіпеда і куба; перевірити засвоєння геометричного матеріалу розділу “Площа прямокутника”, “Об’єм прямокутного паралелепіпеда”. Тип уроку: застосування знань, вмінь та навичок. Хід уроку І. Актуалізація опорних знань Усні вправи 1. Чи існує прямокутний паралелепіпед, 4 грані […]...
- Прямокутний паралелепіпед. Піраміда Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 22. Прямокутний паралелепіпед. Піраміда Рис. 153 Коли ви були маленькими і гралися кубиками, то, можливо, складали фігури, зображені на рисунку 153. Ці фігури дають уявлення про прямокутний паралелепіпед. Форму прямокутного паралелепіпеда мають, наприклад, коробка цукерок, книга, цеглина, коробка сірників, пакувальний […]...
- Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об’єм УРОК 64 Тема. Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об’єм Мета: перевірити засвоєння практичних знань та вмінь учнів з вивчених тем. Тип уроку: перевірка й корекція знань, навичок і вмінь. Обладнання: таблиці “Ділення з остачею”, “Площа прямокутника”, “Об’єм прямокутного паралелепіпеда”. Хід уроку І. Тематична контрольна робота № 5 Варіант 1 1. Виконайте […]...
- Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сторонами a, b і c. – формула периметра трикутника. Сума всіх кутів довільного трикутника дорівнює . Кожний трикутник має принаймні два гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...
- СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...
- Геометричні тіла і многокутники 868. ABCD – тетраедр, 6 ребер, 4 вершини, 4 грані. 869. Многогранник A1A2A3A4A5, 5 граней, 5 вершин, 8 ребер. 870. Многогранник, 5 граней, 6 вершин, 9 ребер. 872. 873. Див. рис. з № 872 S пов. тетр.=36 см2, S грані = 36 : 4 = 9, SABCD = 9 см2, а = ? 874. ABCDA1B1C1D […]...
- Прямокутний паралелепіпед – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Прямокутний паралелепіпед...
- Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини На рисунках, поданих нижче, наведені деякі основні геометричні фігури; поруч даються назви й позначення. Відрізок AB (або BA). Промінь AB. Промінь BA. Пряма AB (або a). Ламана ABСDЕ. Промені AB і АС – доповняльні. Прямі а і b перетинаються. Промені АB і KN перетинаються, AB і CD не […]...
- Підсумкова контрольна робота Урок № 60 Тема. Підсумкова контрольна робота Мета. Перевірити якість засвоєння знань, умінь і навичок учнів по темі “Прямокутний паралелепіпед, куб. Формули об’ємів прямокутного паралелепіпеда і куба”. Розвивати відповідальне відношення до своєї роботи, навички до самостійності. Виховувати в учнів прагнення в досягненні вищих результатів навчання. Тип уроку: урок контролю знань, умінь, навичок. Хід уроку І. […]...
- Многокутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Многокутник На рисунку ABCDE – п’ятикутник. A, B, С, D, E – вершини п’ятикутника; AB, BC, CD, DE, EA – сторони; AC, AD, BE, BD, CE – діагоналі. Окремі види многокутників На рисунках зображені окремі види многокутників. Прямокутник: – формула периметра. – формула площі. Квадрат: – формула периметра. […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
- Пряма призма. Площа поверхні та об’єм призми УРОК № 54 Тема. Пряма призма. Площа поверхні та об’єм призми Мета уроку: повторити, привести в систему й розширити відомості про многогранники, пряму призму, площу поверхні та об’єм призми. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13], моделі прямих призм. Вимоги до рівня підготовки учнів: пояснюють, що таке пряма призма та її […]...
- Об’єм прямокутного паралелепіпеда Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 23. Об’єм прямокутного паралелепіпеда Рис. 173 1 Діагональ паралелепіпеда – це відрізок, що сполучає його вершини, які не належать одній грані. Фігури на рисунку 173, а, б складаються з рівної кількості однакових кубиків. Про такі фігури можна сказати, що їх […]...
- Геометричні фігури на площині Геометричні фігури на площині – Прямокутник – Квадрат 1 Назви множину. Розбий множину многокутників на підмножини. За якою ознакою це можна зробити? Розбий множину чотирикутників на дві підмножини. Розкажи, що ти знаєш про прямокутник. Розбий множину прямокутників на дві підмножини. Розкажи, що ти знаєш про квадрат. Якою фігурою є ABCD? KMNO? Назви пари протилежних сторін […]...
- ПОВТОРЕННЯ. СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР Цілі: – навчальна: повторити поняття степеня натурального числа з натуральним показником; узагальнити знання учнів про площі та об’єми фігур; відтворити вміння розв’язувати задачі на обчислення площі прямокутника і квадрата, об’єму прямокутного паралелепіпеда і куба; – розливальна: формувати вміння аналізувати й узагальнювати інформацію; – виховна: виховувати відповідальність, свідоме ставлення до навчання; Тип уроку: узагальнення та систематизація […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...
- Побудова перерізів многогранників Урок 20 Тема. Побудова перерізів многогранників Мета уроку: формування вмінь учнів застосовувати властивості паралельних площин до розв’язування вправ, побудови перерізів. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Три учні відтворюють розв’язування задач № 28, 30, 31 на дошці, в цей час клас пише математичний диктант. 2. Математичний диктант. Через вершини А, В, […]...
- Поняття об’єму 1121. Цеглина має форму прямокутного паралелепіпеда. Об’єм паралелепіпеда дорівнює: V = 250 × 120 × 65 = 1 950 000 мм3 = 1,95 дм3. 1122. Для того, щоб знайти скільки кубометрів грунту перевернули, треба знайти об’єм прямокутного паралелепіпеда з площею основи 5 га і висотою 35 см. V = 50 000 м2 × 0,35 м […]...
- Об’єми многогранників Геометрія Об’єми тіл Об’єми многогранників Об’єм будь-якої призми дорівнює добутку площі основи та висоти. . На рисунках наведені приклади призм із різними основами. Для прямокутного паралелепіпеда отримаємо , де a, b, c – його виміри. Для куба , де a – довжина ребра. Для похилої призми (рисунок нижче зліва) об’єм можна обчислити як добуток площі […]...
- Геометричні фігури на площині Мета: формувати уявлення про геометричні фігури Дидактичні задачі. Актуалізувати уміння розрізняти прямі, гострі і тупі кути; визначати ці кути у многокутнику; розбивати множини трикутників на підмножини за кутами: ті, що містять один прямий кут, один тупий кут, всі гострі кути; визначати трикутники, в яких всі стороні різної довжини, дві сторони рівні, три сторони рівні; класифікувати […]...
- Геометричні тіла 628. А) спільна вершина; Б) спільне ребро; В) спільна грань; Г) спільна діагональ. 629. А) дві кулі не мають спільних точок; Б) дві кулі мають одну спільну точку; В) дві кулі, які перетинаються; Г) кулі мають різні радіуси і спільний центр. 630. Дано точку О і r > 0, г – відстань. ОХ ≤ r. […]...
- Геометричні фігури в просторі Мета: формувати уявлення про геометричні фігури у просторі Дидактичні задачі. Актуалізувати уявлення про просторові фігури: кулю, циліндр, конус, куб, піраміду, паралелепіпед; уміння визначати в оточуючому середовищі предмети, що мають форму даних фігур. Класифікувати геометричні фігури на просторові та плоскі; актуалізувати уявлення та поняття про плоскі фігури, що обмежують просторові фігури. Формувати уміння розв’язувати задачі з […]...
- Властивості призми 1. 2. 3. Ні, не можна. 4. Бічні ребра перпендикулярні до основи. Усі бічні грані – прямокутники. Бічне ребро є висотою призми. Площа бічної поверхні – добуток периметра Основи на довжину бічного ребра. 5. Так, може. Див. мал. до № 2. 6. 1) Основа правильної призми – правильний багатокутник, Усі бічні грані – рівні прямокутники. […]...
- ПЛОЩА ФІГУРИ. КВАДРАТНИЙ САНТИМЕТР ПЛОЩА ПЛОЩА ФІГУРИ. КВАДРАТНИЙ САНТИМЕТР 617. Обведи тильним кінцем олівця чи ручки контури плоских (площинних) ділянок, зображених на малюнках. 618. Назви плоскі геометричні фігури. 619. Плоскі фігури мають площу. Однакові фігури мають рівні площі. 1) Чи погоджуєшся, що площа круга менша від площі квадрата? Порівняння площ виконано накладанням однієї фігури на іншу. 2) Площа якої […]...
- Найпростіші геометричні фігури та їх властивості Урок № 14 Тема. Найпростіші геометричні фігури та їх властивості Мета: перевірити та оцінити рівень засвоєння знань та вмінь учнів з теми, передбачених програмою; виявити прогалини в знаннях та вміннях учнів для подальшого їх усунення. Тип уроку: перевірка та корекція знань, навичок та вмінь. ХІД УРОКУ І. Умова тематичної контрольної роботи Варіант 1 Початковий рівень […]...
- Величини та їх значення Урок № 57 Тема. Величини та їх значення Мета. Поглибити знання учнів про величини, їх вимірювання та позначення, вчити їх порівнювати, додавати, віднімати, перетворювати. Розвивати здібності учнів через прищеплення інтересу до математики, формувати навички досягнення власної мети. Тип уроку: урок засвоєння нових знань Обладнання: секундомір, спідометр, транспортир, метр, термометр, терези, таблиці “Старі одиниці виміру”, “Залежність […]...
- Прямокутний трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Прямокутний трикутник Теорема Піфагора:...
- ПРЯМОКУТНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 16. ПРЯМОКУТНИЙ ТРИКУТНИК Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°. Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають […]...