Головна ⇒ 📌ГДЗ з математики ⇒ Різниця квадратів двох виразів

Різниця квадратів двох виразів

533. a2 – 144 = (a – 12)(a + 12).

534. -49 + b2 = b2 – 49 = b2 – 72 = (b – 7)(b + 7).

535. 1) а2 – 9 = а2 – 32 = (а – 3)(а + 3);

2) b2 + 1 – не можна розкласти на множники;

3) 4 – с2 = (2 – с)(2 + с);

4) 25 + x2 – не можна розкласти на множники;

5) 1 – y2 = (1 – у)(1 + у);

6) 16а2 – b2 = (4а – b)(4а + b);

7) 81 + 100р2 – не можна розкласти на множники;

8) 81 – 100р2 = (9 – 10р)(9 + 10р);

9) m2n2 – 25 = (mn – 5)(mn + 5);

10) – m2n2 – 25 – не можна розкласти на множники.

Різниця квадратів двох виразів

Різниця квадратів двох виразів

538. 1) x2 – 49 = 0; (х – 7)(х + 7) = 0; х – 7 =

0 або х + 7 = 0; х = 7 або х = -7.

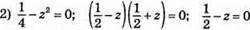Різниця квадратів двох виразів або 1/2 + z = 0; z = 1/2 або z = -1/2.

3) x2 + 36 = 0; х2 = -36; коренів немає.

4) х2 – 0,01 = 0; (х – 0,1)(х + 0,1) = 0; х – 0,1 = 0 або х + 0,1 = 0; х = 0,1 або х = -0,1.

5) 9х2 – 4 = 0; (3х – 2)(3х + 2) = 0; 3х – 2 = 0 або 3х + 2 = 0; 3х = 2 або 3х = -2; х = 2/3 або х = -2/3.

6) 0,04х2 – 1 = 0; (0,2х – 1)(0,2х + 1) = 0; 0,2х – 1 = 0 або 0,2х + 1 = 0; 0,2х = 1 або 0,2х = -1; х = 1 : 0,2 або х = -1 : 0,2; х = 5 або х = -5.

539. 1) с2 – 0,25 = 0; (с – 0,5)(с + 0,5) = 0; с – 0,5 = 0 або с + 0,5 = 0; с = 0,5 або с = -0,5.

2) 81х2 – 121 = 0; (9х – 11)(9х + 11) = 0; 9х – 11 = 0 або 9х + 11 = 0; 9х = 11 або 9х = -11; х = 11/9 або х = -11/9; 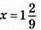Різниця квадратів двох виразів або Різниця квадратів двох виразів

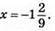
3) -0,09 + 4х2 = 0; (2х – 0,3)(2х + 0,3) = 0;

2х – 0,3 = 0 або 2х + 0,3 = 0; 2х = 0,3 або 2х = -0,3; х = 0,3 : 2 або х = -0,3 : 2; х = 0,15 або х = -0,15.

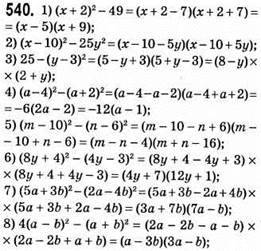
Різниця квадратів двох виразів

Різниця квадратів двох виразів

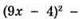
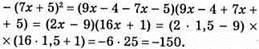
542. 1) Якщо х = 1,5, то Різниця квадратів двох виразів

Різниця квадратів двох виразів

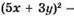
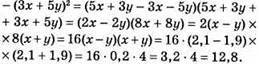
2) Якщо х = 2,1, у = 1,9, то Різниця квадратів двох виразів

Різниця квадратів двох виразів

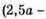
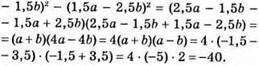
543. Якщо а = -1,5, b = -3,5, то Різниця квадратів двох виразів

Різниця квадратів двох виразів

544. S = a2 – b2. Якщо a = 7,4 CM, b = 2,6 CM, TO S = 7,42 – 2,62 = (7,4 – 2,6) • (7,4 + 2,6) = 4,8 • 10 = 48 (CM2).

Різниця квадратів двох виразів

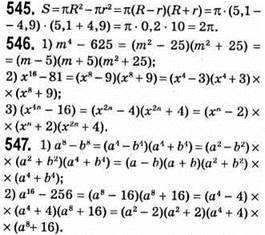
548. 1) (3х – 5)2 – 49 = 0; (3х – 5 + 7) • (3х – 5 – 7) = 0; (3х + 2)(3х – 12) = 0; 3x – 12 = 0 або 3х + 2 = 0; 3x = 12 або 3х = -2; x = 4 або х = -2/3.

2) (4x + 7)2 – 9×2 = 0; (4x + 7 – 3x)(4x + 7 + 3x) = 0; (x + 7)(7x + 7) = 0; X + 7 = 0 або 7х + 7 = 0; х = -7 або 7х = -7; x = -1.

3) (а – 1)2 – (2а + 9)2 = 0; (а – 1 – 2а – 9) • (а – 1 + 2а + 9) = 0; (-а – 10)(3а + 8) = 0; – а – 10 = 0 або 3а + 8 = 0; а = -10 або 3а = -8; а = -10 або 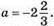Різниця квадратів двох виразів

4) 25(3b + 1)2 – 16(2b – 2)2 = 0; (5(3b + 1) – 4(2b – 1))(5(3b + 1) + 4(2b – 1)) = 0; (15b + 5 – 8b + 4)(15b + 5 + 8b – 4) = 0; (7b + 9)(23b + 1) = 0; 76 + 9 = 0 або 23b + 1 = 0; 7b = -9 або 23b= -1; 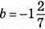Різниця квадратів двох виразів або b = -1/23.

549. 1) 16 – (6 – 11x)2 = 0; (4 – (6 – 11x)) • (4 + (6 – 11x)) = 0; (4 – 6 + 11x)(4 + 6 – 11x) = 0; (11x – 2)(10 – 11x) = 0; 11x – 2 = 0 або 10 – 11x = 0; 11x = 2 або -11x = -10; x = 2/11 або x = 10/11.

2) (7m – 13)2 – (9m + 19)2 = 0; (7m – 13 – 9m – 19)(7m – 13 + 9m + 19) = 0; (-2m – 32)(16m + 6) = 0; -2m – 32 = 0 або 16m + 6 = 0; -2m = 32 або 16m = -6; m = 32 : (-2), або m = -6/16; m =-16 або m = -3/8.

550. 1) (7n + 4)2 – 9 = (7n + 4 – 3)(7n + 4 + 3) = (7n + 1)(7n + 7) = 7(7n + 1)(n + 1) – ділиться націло на 7, бо 7 ділиться на 7.

2) (8n + 1)2 – (3n – 1)2 = (8n + 1 – 3n + 1)(8n + 1 + 3n – 1) = 11n(5n + 2) – ділиться націло на 11, бо 11 ділиться на 11.

3) (3n + 7)2 – (3n – 5)2 = (3n + 7 – 3n + 5)(3n + 7 + 3n – 5) = 12(6n + 2) = 24(3n + 1) – ділиться націло на 24, бо 24 ділиться на 24.

4) (7n + 6)2 – (2n – 9)2 = (7n + 6 – 2n + 9)(7n + 6 + 2n – 9) = (5n + 15)(9n – 3) = 5(n + 3)3(3n – 1) = 15(n + 3)(3n – 1) – ділиться націло на 15, бо 15 ділиться на 15.

551. 1) (5n + 4)2 – (5n – 4)2 = (5n + 4 – 5n + 4)(5n + 4 + 5n – 4) = 8 • 10n = 80n – ділиться націло на 80.

2) (9n + 10)2 – (9n + 8)2 = (9n + 10 – 9n – 8)(9n + 10 + 9n + 8) = 2 • (18n + 18) = 2 • 18(n + 1) = 36 • (n + 1) – ділиться націло на 36.

3) (10n + 2)2 – (4n – 10)2 = (10n + 2 – 4n + 10)(10n + 2 + 4n – 10) = (6n + 12)(14n – 8) = 6(n + 2) • 2(7n – 4) = 12(n + 2)(7n – 4) – ділиться націло на 12.

552. 1) х і х + 1 – два послідовних натуральних числа.

(x + 1)2 – x2 = (x + 1 – x)(x + 1 + x) = 1 • (2x + 1) = 2x + 1 = x + (x + 1).

2) x і (x + 2) – два послідовних парних числа.

(x + 2)2 – x2 = (x + 2 – x)(x + 2 + x) = 2 • (2x + 2) = 2 • 2(x + 1) = 4(x +1) – ділиться націло на 4.

553. 1) (x + 2)2 – x2 = (x + 2 – x)(x + 2 + x) = 2 • (2x + 2) = 2(X + (X + 2));

2) 2n + 1, 2n + 3 – послідовні непарні числа.

(2n + 3)2 – (2n + 1)2 = (2n + 3 – 2n – 1)(2n + 3 + 2n + 1) = 2 • (4n + 4) = 8(n + 1) – ділиться націло на 8.

554. (m3 – n3)2(m3 + n3)2 – (m6 + n6)2 = -4m6n6 – ТОТОЖНІСТЬ;

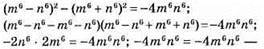Різниця квадратів двох виразівПравильна рівність.

555. Нехай 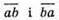Різниця квадратів двох виразів – шукані числа, тоді

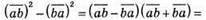
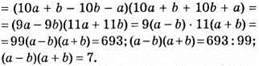
Різниця квадратів двох виразів

Різниця квадратів двох виразів

Оскільки а і b – натуральні числа, а 7 розкладається лише на множники 1 і 7, то а – b = 1, тобто а і b – сусідні цифри і а + b = 7. Отже, а = 3, b = 4 або навпаки.

Тобто: 34 і 43 – шукані числа.

556. а = 7n + 4, b = 7k + 3, тоді а2 – b2 = (7n + 4)2 – (7k + 3)2 = (7n + 4 – 7k – 3)(7n + 4 + 7k + 3) = (7k – 7k + 1)(7n + 7k + 7) = 7(7n – 7k + 1)(n + k + 1) кратне 7, бо 7 кратне 7.

557. (b2 – 4)x = b – 2; (b – 2)(b + 2)x = b – 2.

1) При b = 2 рівняння має вигляд 0 • x = 0 і має безліч коренів.

2) При b = -2 рівняння має вигляд 0 • x = -4 і не має коренів.

3) При b ≠ 2 і b ≠ -2 рівняння має один корінь.

558. (а2 – 25)x = а + 5; (а – 5)(а + 5)x = а + 5.

1) При а = -5 рівняння має вигляд 0 • x = 0 і має безліч коренів.

2) При а = 5 рівняння має вигляд 0 • x = 10 і не має коренів.

3) При а ≠ 5 і а ≠ -5 рівняння має один корінь.

559. Нехай власна швидкість човна х км/год, тоді швидкість човна за течією (х + 2,5) км/год, а проти течії – (х – 2,5) км/год. За течією річки човен пройшов 2,4(х + 2,5) км, а проти течії річки – 3,6(х – 2,5)км. За умовою 2,4(х + 2,5) – 3,6(х – 2,5) = 5,4; 2,4х + 6 – 3,6х + 9 = 5,4; 2,4х – 3,6x = 5,4 – 6 – 9; -1,2x = -9,6; x = -9,6 : (-1,2); x = 8 км/год – власна швидкість човна.

560. Нехай першого дня продали x кг апельсинів, тоді другого дня продали 4/9x кг апельсинів, а третього дня – 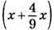Різниця квадратів двох виразів кг апельсинів. За 3 дні продали 130 кг апельсинів.

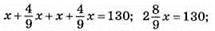
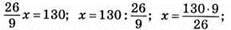
Отже, Різниця квадратів двох виразівРізниця квадратів двох виразів

Х = 45 кг апельсинів продали за перший день.

Різниця квадратів двох виразів

Будь-яке число є коренем рівняння.

563. 1) а < 3а в 3 рази. Дана умова виконується при будь-якому додатному значенні а.

2) а2 < 3а2 в 3 рази. Дана умова виконується при будь-якому значенні а, крім а = 0.

3) а2 + 1 < 3а2 + 3 в 3 рази, тоді 3(а2 + 1) = 3а2 + 3; 3а2 + 3 = 3а2 + 3, або 0 = 0. Дана умова виконується при будь-якому значенні а.

Різниця квадратів двох виразів


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Сума й різниця кубів двох виразів 682. 1) Якщо b = -2, то (1 – b2)(1 + b2 + b4) = 1 – (b2)3 = 1 – b6 = 1 – (-2)6 = 1 – 64 = -63. 2) Якщо х = -1, то 2х3 + 7 – (х + 1)(х2 – х + 1) = 2х3 + 7 – (х3 […]...

  2. Різниця квадратів. (Добуток різниці двох виразів на їх суму) Урок № 46 Тема. Різниця квадратів (Добуток різниці двох виразів на їх суму) Мета: відпрацювати навички застосування формули (a – b)(a + b) = a2 – b2 для перетворення цілих виразів у багаточлен стандартного вигляду із застосуванням переставного та сполучного законів множення та залежностей між знаком множників та добутком цих множників; поглибити знання та вміння […]...

  3. Розкладання на множники різниці квадратів двох виразів Розділ 1. ЦІЛІ ВИРАЗИ & 16. Розкладання на множники різниці квадратів двох виразів У тотожності (а – b)(а + b) = а2 – b2 поміняємо місцями ліву і праву частини. Матимемо: Цю тотожність називають формулою різниці квадратів двох виразів. Читають її так. Формулу різниці квадратів двох виразів застосовують для розкладання на множники двочлена а2 – […]...

  4. Добуток різниці та суми двох виразів Рівняння коренів не має; Коренем рівняння є будь-яке число; Отже, значення виразу не залежить від значення змінної. 2) (2a – b)(2a + b) + (b – с)(b + с) + (с – 2а)(с + 2а) = 4а2 – b2 + b2 – с2 + с2 – 4а2 = 0. Отже, значення виразу не залежить від […]...

  5. РІЗНИЦЯ КВАДРАТІВ РОЗДІЛ 3 МНОГОЧЛЕНИ &12. РІЗНИЦЯ КВАДРАТІВ Ви вже знаєте, що таке формули скороченого множення, і вмієте користуватися формулами квадрата суми двох одночленів і квадрата різниці двох одночленів. Ще одну формулу дістанемо, довівши наступну теорему. Запам’ятайте! Теорема (про добуток суми і різниці двох одночленів). Добуток суми і різниці двох одночленів дорівнює різниці їх квадратів: (а + […]...

  6. Квадрат суми та квадрат різниці двох виразів 567. (5а + 3)2 = 25а2 + 30а + 9. 568. Тотожності: 3) (12а – b)2= 144а2 – 24аb + b2. Рівняння коренів не має. 577. (a – b)2 = (b – a)2 – тотожність, бо (a – b)2 = a2 – 2ab + b2; (b – a)2 = b2 – 2ab + a2, a […]...

  7. РІЗНИЦЯ КВАДРАТІВ Цілі: – навчальна: сформувати стійкі вміння і навички застосовувати формулу різниці квадратів до розв’язування задач; – розвивальна: формувати вміння використовувати необхідну інформацію для розв’язування задач; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати відповідальність за результати своєї роботи, дисциплінованість, працьовитість; Тип уроку : застосування знань, умінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП […]...

  8. Сума і різниця кубів 645. Твердження 3). 646. 1) Ні; 2) ні; 3) так; 4) ні. 647. 1) Так; 2) ні; 3) ні; 4) ні. 648. 1) Ні; 2) так; 3) ні; 4) ні. 649. 1) Так; 2) ні; 3) ні; 4) ні. 650. (х + у)(х2 – ху + у2) = х3 + у3. 651. 1) Ні; 2) […]...

  9. Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...

  10. Множення різниці двох виразів на їх суму Розділ 1. ЦІЛІ ВИРАЗИ & 15. Множення різниці двох виразів на їх суму Помножимо різницю а – b на суму а + b: (а – b)(а + b) = а2 + ab – bа – b2 = а2 – b2. Отже, Одержали ще одну формулу скороченого множення. Її читають так. Розглянемо приклади застосування цієї формули. […]...

  11. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ПЕРЕТВОРЕННЯ ВИРАЗІВ Цілі: – навчальна: удосконалити вміння застосовувати перетворення виразів до розв’язування задач; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати культуру усного та писемного мовлення; – виховна: виховувати старанність, дисциплінованість, працьовитість; Тип уроку : удосконалення і застосування знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ […]...

  12. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ НА СУМІСНІ ДІЇ. ЗАДАЧІ НА ЗУСТРІЧНИЙ РУХ ДВОХ ТІЛ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: УЧИТИ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА ЗУСТРІЧНИЙ ОДНОЧАСНИЙ РУХ; ЗАКРІПЛЮВАТИ ВМІННЯ ЗНАХОДИТИ ЗНАЧЕННЯ ВИРАЗІВ НА СУМІСНІ ДІЇ І. Перевірка домашнього завдання 1. Серед записаних на дошці виразів знайти той, яким розв’язується задача 713. 294 • 2 : 7 • 6 294 : 7 : 2 • 6 294 : 2 : 7 • 6 […]...

  13. Розкладання многочлена на многочлени. Винесення спільного множника за дужки 437. 1) Якщо х = 4,32, то 6,32х – х2 = х(6,32 – х) = 4,32 • (6,32 – 4,32) = 4,32 • 2 = 8,64. 2) Якщо а = 1,5, b = -2,5, то а3 + а2b = а2(а + b) = 1,52 • (1,5 – 2,5) = 2,25 • (-1) = -2,25. 3) […]...

  14. РОБОТА В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ. ПОТЕНЦІАЛ ПОЛЯ. РІЗНИЦЯ ПОТЕНЦІАЛІВ ДВОХ ТОЧОК ПОЛЯ Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 1. ОСНОВИ ЕЛЕКТРОСТАТИКИ 1.5. РОБОТА В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ. ПОТЕНЦІАЛ ПОЛЯ. РІЗНИЦЯ ПОТЕНЦІАЛІВ ДВОХ ТОЧОК ПОЛЯ Робота в електростатичному полі: – не залежить від шляху, а визначається координатами точок, між якими переноситься заряд; – у будь-якому замкненому контурі дорівнює нулю. Такі поля називаються потенціальними. Потенціал поля (φ) у даній […]...

  15. Одночлени 261. Одночлени: 262. В стандартному вигляді записані: 263. 1) 5а і 7a – подібні одночлени; 2) 3a2b2c і 6a2b2c – подібні одночлени; 3) 8х2у4 і 8х2у5 – не є подібними; 4) 3у2 і 2у3 – не є подібними; 5) 1/2m7n8 і 1/2m8n7 – не є подібними; 6) -0,1а°610 і 0,1а9610 – подібні одночлени. 264. 1) […]...

  16. Розкладання многочлена на множники. Метод групування 480. 1) Якщо a = 0,5; b = 2,25, то 2a3 – 3a2 – 2ab + 3b = (2a3 – 3a2) – (2ab – 3b) = a2(2a – 3) – b(2a – 3) = (2a – 3)(a2 – b) = (2 • 0,5 – 3) • (0,52 – 2,25) = (1 – 3) • (0,25 […]...

  17. СУМА І РІЗНИЦЯ КУБІВ РОЗДІЛ 3 МНОГОЧЛЕНИ &13. СУМА І РІЗНИЦЯ КУБІВ Перелік формул скороченого множення, які ви знаєте, у цьому параграфі доповнимо ще двома формулами. Для цього спочаткy доведемо наступну теорему. Запам’ятайте! Теорема 1 (про добуток суми двох одночленів і неповного квадрата їх різниці). Добуток суми двох одночленів і неповного квадрата їх різниці дорівнює сумі кубів цих одночленів: […]...

  18. Розв’язування вправ на застосування перетворень виразів Урок № 56 Тема. Розв’язування вправ на застосування перетворень виразів Мета: узагальнити та систематизувати знання та вміння учнів щодо різних видів перетворень цілих виразів; відпрацювати навички застосування набутих знань та вмінь під час розв’язування завдань на доведення подільності. Тип уроку: узагальнення та систематизація знань. Хід уроку I. Організаційний момент Перевіряємо готовність учнів до уроку, повідомляємо […]...

  19. СУМА Й РІЗНИЦЯ КУБІВ Цілі: – навчальна: удосконалити вміння застосовувати формули суми й різниці кубів до розв’язування задач; – розвивальна: формувати вміння міркувати за аналогією; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати позитивне ставлення до навчання, віру у власні сили, цілеспрямованість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ […]...

  20. Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...

  21. Повторення та систематизація матеріалу, вивченого в 7 класі. Перетворення виразів Урок № 83 Тема. Повторення та систематизація матеріалу, вивченого в 7 класі. Перетворення виразів Мета: повторити та систематизувати знання про види та способи перетворення буквених виразів, вивчених у 7 класі; повторити та вдосконалити вміння використовувати набуті знання під час розв’язування типових вправ. Тип уроку: повторення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент […]...

  22. Сума та різниця кубів Урок № 47 Тема. Сума та різниця кубів Мета: домогтися свідомого засвоєння змісту формул (a ± b)(a2 ab + b2) = a3 ± b3 та виробити базові вміння застосовувати ці формули для перетворень відповідних цілих виразів у багаточлен стандартного вигляду. Тип уроку: засвоєння знань. Хід уроку I. Організаційний момент @ Учитель перевіряє готовність учнів до […]...

  23. Знаходження значень виразів на сумісні дії першого ступеня та виразів з дужками. Задачі з буквеними даними (№№ 421-430) Тема. Знаходження значень виразів на сумісні дії першого ступеня та виразів з дужками. Задачі з буквеними даними (№№ 421-430). Мета. Закріплювати вміння учнів виконувати дії додавання і віднімання над багатоцифровими числами; навчати узагальнених прийомів розв’язування задач. Обладнання. Таблиця усних обчислень; картки для опитування; схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка […]...

  24. ПОРІВНЯННЯ ВИРАЗІВ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ДВІ ДІЇ РІЗНИХ СТУПЕНІВ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ І ДІЛЕННЯ Урок 56. ПОРІВНЯННЯ ВИРАЗІВ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ НА ДВІ ДІЇ РІЗНИХ СТУПЕНІВ Мета: вдосконалювати обчислювальні навички, вміння розв’язувати прості і складені задачі на множення; закріплювати табличні випадки множення числа 2, вміння порівнювати числові вирази, знаходити значення виразів; розвивати логічне мислення; виховувати пізнавальний інтерес. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ […]...

  25. Таблиця квадратів натуральних чисел від 10 до 99 10. Додатки 31. Таблиця квадратів натуральних чисел від 10 до 99 Десятки Одиниці 0 1 2 3 4 5 6 7 8 9 1 100 121 144 169 196 225 256 289 324 361 2 400 441 484 529 576 625 676 729 784 841 3 900 961 1024 1089 1156 125 1296 1369 1444 […]...

  26. Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...

  27. Система двох лінійних рівнянь із двома невідомими – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Система двох лінійних рівнянь із двома невідомими – сталі. Правило Крамера: Квадратний тричлен – тричлен виду у = ах2 + bх + с, де х – змінна, а, b, с – константи і а ≠ 0. Одночлен ах2 називають старшим членом квадратного тричлена, а коефіцієнт а – старшим коефіцієнтом. Квадратний […]...

  28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...

  29. Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...

  30. Застосування різних способів розкладання многочлена на множники Немає коренів. Немає коренів. 726. 1) х3 – х = 0; х(х2 – 1) = 0; х(х – 1)(х + 1) = 0; х = 0 або х – 1 = 0; х = 1 або х + 1 = 0; х = -1. 2) х4 + х2 = 0; х2(х2 + 1) = 0; […]...

  31. ОБЧИСЛЕННЯ ВИРАЗІВ НА СУМІСНІ ДІЇ З БАГАТОЦИФРОВИМИ ЧИСЛАМИ. РІВНЯННЯ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: УДОСКОНАЛЮВАТИ ОБЧИСЛЮВАЛЬНІ НАВИЧКИ, УМІННЯ СКЛАДАТИ ТА РОЗВ’ЯЗУВАТИ РІВНЯННЯ Й ЗАДАЧІ НА ЗНАХОДЖЕННЯ ПЛОЩІ ПРЯМОКУТНИКА ТА ОБЕРНЕНІ ДО НИХ I. Перевірка домашнього завдання Взаємоперевірка виконаних удома завдань. II. Актуалізація та корекція опорних знань учнів 1. Завдання для опитування. 1) Обчислити: (15 504 : 38 + 29 108) • 34. 2) Скільки годин пройшло […]...

  32. Перетворення виразів Уроки № 122, 123 Тема. Перетворення виразів 1. Спростіть вираз і знайдіть його значення при даних значеннях букв: а) -12b – 7b + 10b – b при b = -0,1; 2; -1; -5,7; 0; Б) -5а – 8а – 2а – 15a при а = -0,6; ; ; 0,002; -1; В) -4c + 9с – […]...

  33. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...

  34. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...

  35. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  36. Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...

  37. Множення многочлена на многочлен 0x = -1: рівняння коренів не має. Коренем рівняння є будь-яке число. Отже, значення виразу не залежить від змінної. 404. (х – 3)(х2 + 7) – (х – 2)(х2 – х + 5) = х3 – 3х2 + 7х – 21 – (х3 – х2 + 5х – 2х2 + 2х – 10) = х3 […]...

  38. Потенціал і різниця потенціалів ЕЛЕКТРОДИНАМІКА Електричне поле. Електричний струм УРОК 3/3 Тема. Потенціал і різниця потенціалів Мета уроку: ознайомити учнів з енергетичною характеристикою електричного поля. Тип уроку: комбінований урок. ПЛАН УРОКУ Контроль знань 15 хв. Самостійна робота № 1 “Напруженість електричного поля. Речовина в електричному полі” Демонстрації 3 хв. 1. Вимірювання різниці потенціалів. 2. Еквіпотенціальні поверхні Вивчення нового матеріалу […]...

  39. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ НА СУМІСНІ ДІЇ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ФОРМУВАТИ ОБЧИСЛЮВАЛЬНІ НАВИЧКИ, ЗАКРІПЛЮВАТИ ВМІННЯ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА СПІЛЬНУ РОБОТУ ТА РІВНЯННЯ І. Перевірка домашнього завдання Фронтально перевірити план та пояснити вибір дій у задачі 1058. У вправі 1057 вибірково пояснити виконання дій. ІІ. Актуалізація та корекція опорних знань учнів 1. Завдання для опитування. 1) Обчислити: 2 т 60 кг • 51; […]...

  40. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...

Ви зараз читаєте: Різниця квадратів двох виразів
«
»